黑龙江省牡丹江市林口县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. 若关于x的方程（a﹣2）x²﹣1＝0是一元二次方程，则a的取值范围是（）

A、a≠0 B、a＞2 C、a＜2 D、a≠2

查看试题解析
2. 我国是一个多民族国家，民俗文化丰富多彩．下面是几幅具有浓厚民族特色的图案，其中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 方程x²﹣1＝0的解是（）

A、x＝﹣1 B、x＝1 C、x＝﹣1或x＝1 D、x＝1或x＝0

查看试题解析
4. 下列成语所描述的事件是随机事件的是（）

A、瓮中捉鳖 B、守株待兔 C、水涨船高 D、水中捞月

查看试题解析
5. 下列抛物线中，其顶点在反比例函数y＝ $\frac{12}{x}$ 的图象上的是（）

A、y＝（x﹣4）²+3 B、y＝（x﹣4）²﹣3 C、y＝（x+2）²+1 D、y＝（x+2）²﹣1

查看试题解析
6. 如图， $A B$ 为 $⊙ O$ 的直径， $C ， D$ 为 $⊙ O$ 上两点，若 $∠ B C D ＝ 40 °$ ，则 $∠ A B D$ 的大小为（）．

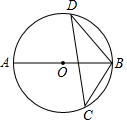A、60° B、50° C、40° D、20°

查看试题解析
7. 已知 $Δ A B C \sim Δ D E F$ 且对应中线之比为 $9 ： 16$ ，则 $Δ A B C$ 与 $Δ D E F$ 的周长之比为 $($ 　　 $)$

A、 $4 ： 3$ B、 $3 ： 4$ C、 $16 ： 9$ D、 $9 ： 16$

查看试题解析
8. 某年级举办篮球友谊赛，参赛的每两个队之间都要比赛一场，共要比赛28场，则参加此次比赛的球队数是（）

A、6 B、7 C、8 D、9

查看试题解析
9. 已知圆心角为120°的扇形的弧长为6π，该扇形的面积为（）

A、 $18 π$ B、 $27 π$ C、 $36 π$ D、 $54 π$

查看试题解析
10. 如图是抛物线型拱桥，当拱顶高离水面2m时，水面宽4m.水面上升1.5m，水面宽度为（）

A、1m B、2m C、 $\sqrt{3}$ m D、 $2 \sqrt{3}$ m

查看试题解析
11. 如图，Rt△ABC中，∠A＝30°，∠ABC＝90°．将Rt△ABC绕点B逆时针方向旋转得到 $△ A^{'} B C^{'}$ ．此时恰好点C在 $A^{'} C^{'}$ 上， $A^{'} B$ 交AC于点E，则△ABE与△ABC的面积之比为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
12. 如图，抛物线y＝ax²+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x＝﹣ $\frac{1}{2}$ ，结合图象分析下列结论：
①abc＞0；

②3a+c＞0；

③当x＜0时，y随x的增大而增大；

④ $\frac{b^{2} - 4 a c}{4 a}$ ＜0；

⑤若m ， n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根，则m＜﹣3且n＞2．

其中正确的结论有（　　）

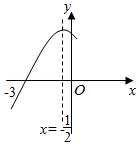A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

13. 在平面直角坐标系中，点A（-4，1）关于原点对称的点的坐标是.

查看试题解析
14. 如果 $x = 2$ 是方程 $x^{2} - c = 0$ 的一个根，这个方程的另一个根为.

查看试题解析
15. 将抛物线 $y = x^{2}$ 先向右平移1个单位长度，再向上平移2个单位长度，得到的抛物线的解析式是.

查看试题解析
16. 若关于x的方程x²+2x﹣m＝0（m是常数）有两个相等的实数根，则反比例函数y＝ $\frac{m}{x}$ 经过第象限．

查看试题解析
17. 如图，⊙O是△ABC的外接圆，∠A＝60°，BC＝6 $\sqrt{3}$ ，则⊙O的半径是．

查看试题解析
18. 如图，□ABCD中，点E是AD边的中点，BE交对角线AC于点F，若AF=2，则对角线AC长为

查看试题解析
19. 在半径为3cm的⊙O中，若弦AB=3 $\sqrt{2}$ ，则弦AB所对的圆周角度数为.

查看试题解析
20. 如图，在正方形ABCD中，AB＝a，点E，F在对角线BD上，且∠ECF＝∠ABD，将△BCE绕点C旋转一定角度后，得到△DCG，连接FG．则下列结论：
①∠FCG＝∠CDG；

②△CEF的面积等于 $\frac{1}{4} a^{2}$ ；

③FC平分∠BFG；

④BE²+DF²＝EF²；

其中正确的结论是．（填写所有正确结论的序号）

查看试题解析

三、解答题

21.

(1)、用配方法解方程： x²＋4x﹣3＝0

(2)、先化简，再求值： $(\frac{4}{x^{2} - 4} - \frac{2}{x + 2}) \div \frac{x^{2} - 4 x}{x - 2}$ ，其中x²＋2x﹣8＝0

查看试题解析
22. 如图抛物线y=x²+bx-c经过直线y=x-3与坐标轴的两个交点A，B，与x轴交于另一点C，抛物线的顶点为D．

(1)、求此抛物线的解析式；

(2)、求S_△ACD的面积．

查看试题解析
23. 如图， $△ A B C$ 内接于 $⊙ O$ ， $∠ B = 60 °$ ，点E在直径CD的延长线上，且 $A E = A C$ .

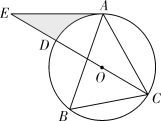(1)、试判断AE与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $A C = 6$ ，求阴影部分的面积.

查看试题解析
24. 为庆祝建国 $70$ 周年，东营市某中学决定举办校园艺术节．学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加．为了了解报名情况，组委会在全校随机抽取了若干名学生进行问卷调查，现将报名情况绘制成如图所示的不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

(1)、在这次调查中，一共抽取了多少名学生？

(2)、补全条形统计图；

(3)、在扇形统计图中，求“声乐”类对应扇形圆心角的度数；

(4)、小东和小颖报名参加“器乐”类比赛，现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器，用列表法或画树状图法求出他们选中同一种乐器的概率．

查看试题解析
25. “互联网+”时代，网上购物备受消费者青睐，某网店专售一款体恤衫，其成本为每件80元，当售价为每件140元时，每月可销售100条，为了吸引更多顾客，该网店采取降价措施，据市场调查反映：销售单价每降1元，则每月可多销售5件，设每件体恤衫的售价为x元（x为正整数），每月的销售量为y件.

(1)、直接写出y与x的函数关系式；

(2)、设该网店每月获得的利润为w元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定每月从利润中捐出400元资助贫困学生，为了保证捐款后每月利润不低于7475元，且让消费者得到最大的实惠，该如何确定体恤衫的销售单价？

查看试题解析
26. 已知 $Δ A B C$ 中， $A B = A C$ ，D、E是 $B C$ 边上的点，将 $Δ A B D$ 绕点A旋转，得到 $Δ A C D^{'}$ ，连结 $D^{'} E$ ．

(1)、如图1，当 $∠ B A C = 120 °$ ， $∠ D A E = 60 °$ 时，求 $∠ D^{'} A E$ 的度数；

(2)、如图2，当 $D E = D^{'} E$ 时，求证： $∠ D A E = \frac{1}{2}$ $∠ B A C$ ．

(3)、如图3，在（2）的结论下，当 $∠ B A C = 90 °$ ， $B D$ 与 $D E$ 满足怎样的数量关系时，△ $D^{'} E C$ 是等腰直角三角形？（直接写出结论，不必说明理由）

查看试题解析