黑龙江省佳木斯市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-29 类型:期末考试
一、单选题
-
1. 下列四个图形中,可以由一个“基本图案”连续旋转 得到的是( )A、
 B、
B、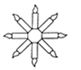 C、
C、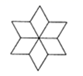 D、
D、 2. 下列事件中是不可能事件的为( )A、抛掷一石头,石头终将落地 B、从装有黑球、白球的袋里摸出红球 C、地球绕着太阳转 D、买1张彩票,中 万大奖3. 我们解方程3x2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程:3x=0或x-2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )A、函数思想 B、数形结合思想 C、公理化思想 D、转化思想4. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
2. 下列事件中是不可能事件的为( )A、抛掷一石头,石头终将落地 B、从装有黑球、白球的袋里摸出红球 C、地球绕着太阳转 D、买1张彩票,中 万大奖3. 我们解方程3x2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程:3x=0或x-2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )A、函数思想 B、数形结合思想 C、公理化思想 D、转化思想4. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )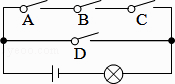 A、 B、 C、 D、5. 已知⊙ 的半径等于 ,圆心 到直线 的距离为 ,则直线 与⊙ 的位置关系是( )A、相离 B、相切 C、相交 D、无法判断6. 如图, , , 为圆上的三点, , 点可能是圆心的是( )A、
A、 B、 C、 D、5. 已知⊙ 的半径等于 ,圆心 到直线 的距离为 ,则直线 与⊙ 的位置关系是( )A、相离 B、相切 C、相交 D、无法判断6. 如图, , , 为圆上的三点, , 点可能是圆心的是( )A、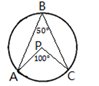 B、
B、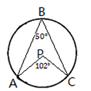 C、
C、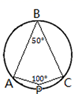 D、
D、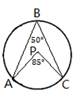 7. 将抛物线y=3x2+2向左平移2个单位长度,再向下平移3个单位长度,则得到的抛物线的解析式为( )A、y=3(x﹣2)2﹣1 B、y=3(x﹣2)2+5 C、y=3(x+2)2﹣1 D、y=3(x+2)2+58. 某校九年(一)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了2070张相片.如果全班有 名学生,根据题意,列出的方程为( )A、 B、 C、 D、9. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、
7. 将抛物线y=3x2+2向左平移2个单位长度,再向下平移3个单位长度,则得到的抛物线的解析式为( )A、y=3(x﹣2)2﹣1 B、y=3(x﹣2)2+5 C、y=3(x+2)2﹣1 D、y=3(x+2)2+58. 某校九年(一)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了2070张相片.如果全班有 名学生,根据题意,列出的方程为( )A、 B、 C、 D、9. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、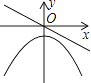 B、
B、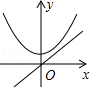 C、
C、 D、
D、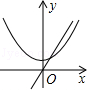 10. 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连结PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( )
10. 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连结PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
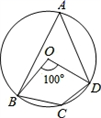
11. 若 是关于 的一元二次方程,则 的取值范围是为 .12. 请写出一个开口向上,并且与 轴交于点 的抛物线解析式 .13. 已知三角形的内切圆半径为 ,三角形的周长为 ,则该三角形的面积为 .14. 已知 是方程 的一个根,则方程的另一个根是 .15. 某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2 , 该型号飞机着陆后滑行m才能停下来.16. 设 , , 是抛物线 上的三点,则 , , 的大小关系为 .17. ⊙ 的半径为5cm,AB、CD是⊙ 的两条弦, , , .则 和 之间的距离为 .18. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD= 100°,则∠BCD=.
 19. 某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来约有粒.
19. 某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来约有粒.
20. 如图,直线 与 轴、 轴分别交于 , 两点,将 绕点 逆时针旋转 后得到 ,则点 的坐标是 .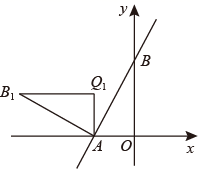
三、解答题
-
21. 解方程(1)、 ;(2)、22. 某水果店销售一种水果的成本价是5元/千克,在销售中发现,当这种水果的价格定为7元/千克时,每天可以卖出160千克,在此基础上,这种水果的单价每提高1元/千克,该水果店每天就会少卖出20千克,设这种水果的单价为 元( ),(1)、请用含 的代数式表示:每千克水果的利润元及每天的销售量千克.(2)、若该水果店一天销售这种水果所获得的利润是420元,为了让利于顾客,单价应定为多少元?23. 已知抛物线 与 轴相交于 , 两点(点 在点 的左侧),顶点为 .
 (1)、求 , , 三点的坐标;(2)、在平面直角坐标系内画出此抛物线的简图,并根据简图写出当 取何值时,函数值大于 .24. 如图,⊙ 与 的边 相切于点 ,与 相交于点 ,且 ,
(1)、求 , , 三点的坐标;(2)、在平面直角坐标系内画出此抛物线的简图,并根据简图写出当 取何值时,函数值大于 .24. 如图,⊙ 与 的边 相切于点 ,与 相交于点 ,且 ,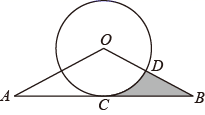 (1)、求劣弧 的长;(2)、求图中阴影部分的面积.25. 甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数;(2)、你认为这个游戏对双方公平吗?请说明理由.26. 如图, 是等边三角形 内一点,将线段 绕点 顺时针旋转60°得到线段 ,连接 , , .若 , , ,求四边形 的面积.
(1)、求劣弧 的长;(2)、求图中阴影部分的面积.25. 甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数;(2)、你认为这个游戏对双方公平吗?请说明理由.26. 如图, 是等边三角形 内一点,将线段 绕点 顺时针旋转60°得到线段 ,连接 , , .若 , , ,求四边形 的面积. 27. 已知 是⊙ 的直径,点 在 的延长线上, , , 是⊙ 上半部分的一个动点,连接 , .(1)、如图①, 的最大面积是;
27. 已知 是⊙ 的直径,点 在 的延长线上, , , 是⊙ 上半部分的一个动点,连接 , .(1)、如图①, 的最大面积是;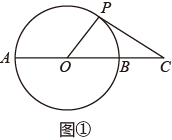 (2)、如图②,延长 交⊙ 于点 ,连接 ,当 时,求证: 是⊙ 的切线.
(2)、如图②,延长 交⊙ 于点 ,连接 ,当 时,求证: 是⊙ 的切线.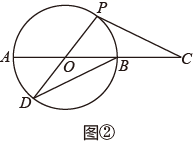 28. 小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”,小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图:
28. 小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”,小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图: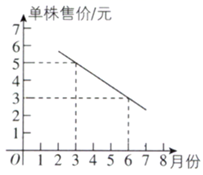
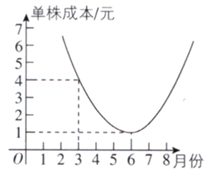 (1)、如果在3月份出售这种植物,单株获利元;(2)、单株售价 与月份x之间的关系式为;单株成本 与月份x之间的关系式为 .(3)、请你运用所学知识,帮助小哲的姑妈求出在哪个月销售这种“多肉植物”,单株获利最大(提示:单株获利=单株售价-单株成本).
(1)、如果在3月份出售这种植物,单株获利元;(2)、单株售价 与月份x之间的关系式为;单株成本 与月份x之间的关系式为 .(3)、请你运用所学知识,帮助小哲的姑妈求出在哪个月销售这种“多肉植物”,单株获利最大(提示:单株获利=单株售价-单株成本).