黑龙江省哈尔滨市阿城区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. $\frac{1}{2021}$ 的倒数是（）

A、 $- \frac{1}{2021}$ B、 $\frac{1}{2021}$ C、 $- 2021$ D、2021

查看试题解析
2. 下列计算正确的是（）

A、a²+a³=a⁵ B、m⁵÷m³=m² C、（x²）⁴=x⁶ D、（a﹣b） ²=a²﹣b²

查看试题解析
3. 下列图形中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图，正确的是（）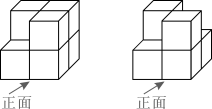

A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同

查看试题解析
5. 如图，AB是⊙O的直径，BC是⊙O的弦，已知∠AOC＝80°，则∠ABC的度数为（）

A、20° B、30° C、40° D、50°

查看试题解析
6. 将抛物线 $y = x^{2}$ 向右平移1个单位，再向上平移3个单位后，它的解析式为（）

A、 $y = {(x + 1)}^{2} + 3$ B、 $y = {(x - 1)}^{2} + 3$ C、 $y = {(x + 1)}^{2} - 3$ D、 $y = {(x - 1)}^{2} - 3$

查看试题解析
7. 如图，已知钝角三角形ABC，将△ABC绕点A按逆时针方向旋转110°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（）

A、55° B、65° C、85° D、75°

查看试题解析
8. 分式方程 $\frac{3}{x + 1} = \frac{2}{x - 1}$ 的解是（）

A、x＝5 B、x＝﹣1 C、x＝1 D、x＝﹣5

查看试题解析
9. 一个不透明的盒子中装有 $5$ 个红球， $3$ 个白球和 $2$ 个黄球，这些球除了颜色外无其他差别，从中随机摸出一个小球，恰好是白球的可能性为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{10}$ C、 $\frac{1}{5}$ D、 $\frac{1}{3}$

查看试题解析
10. 如图，在 $△ A B C$ 中，D、E分别在边AB、AC上， $D E / / B C$ ， $E F / / C D$ 交AB于F ，那么下列比例式中正确的是 $($ ）

A、 $\frac{A F}{D F} = \frac{D E}{B C}$ B、 $\frac{D F}{D B} = \frac{A F}{D F}$ C、 $\frac{E F}{C D} = \frac{D E}{B C}$ D、 $\frac{A F}{B D} = \frac{A D}{A B}$

查看试题解析

二、填空题

11. 根据世界卫生组织最新统计数据报道，截止到2020年12月2日全球累计“新冠肺炎”确诊病例已经超过63000000例，请将 63 000 000用科学记法表示为.

查看试题解析
12. 在函数 $y = - \sqrt{x + 3}$ 中，自变量x的取值范围是．

查看试题解析
13. 反比例函数 $y = \frac{m - 2}{x}$ 的图象在第二、四象限，那么实数m的取值范围是；

查看试题解析
14. 计算： $\sqrt{24} - 6 \sqrt{\frac{1}{6}}$ 的结果是．

查看试题解析
15. 因式分解：a³﹣2a²b+ab²= ．

查看试题解析
16. 抛物线 $y = - 3 x^{2} + 6 x + 2$ 的对称轴为直线：．

查看试题解析
17. 不等式组 ${\begin{array}{l} 2 x + 2 > 3 (x - 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ 的解为.

查看试题解析
18. 已知扇形的圆心角为150°，它的面积为240πcm² ，那么扇形的半径为．

查看试题解析
19. 已知正方形ABCD中，点E在CD边上，AD＝3，DE＝2，将线段AE绕点A旋转，使点E落在直线BC上的点F处，则DF的长为．

查看试题解析
20. 如图，在△ABC中，∠ACB＝90°，点D为AB的中点，AC＝3， $\cos ∠ C A B = \frac{1}{3}$ ，将△DAC沿着CD折叠后，点A落在点E处，则BE的长为．

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{1}{a - 1} - \frac{a - 1}{a^{2} + 2 a + 1} \div \frac{a - 1}{a + 1}$ ，其中a＝2tan60°•sin30°．

查看试题解析
22. 如图是由边长为1的小正方形构成的网格（下面所画三角形顶点都在小正方形顶点上）．

(1)、在图1中画出以AB为直角边的等腰直角三角形ABC，并且直接写出线段BC的长度；

(2)、在图2中画出一个以DE为一腰的等腰三角形DEF，使S_△DEF＝8．

查看试题解析
23. 以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛．某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机的抽取了部分新聘毕业生的专业情况进行调查，并将调查结果绘制成如下两幅不完整的统计图，根据已知信息，解答下列问题：

(1)、求本次共抽查了多少名新聘毕业生；

(2)、请补全形统计图；

(3)、该公司新聘600名毕业生，请你估计“软件”专业的毕业生有多少名．

查看试题解析
24. 如图，点E，F分别在菱形ABCD的边BC，CD上，且BE＝DF．

(1)、如图1，求证：∠BAF＝∠DAE；

(2)、如图2，若∠ABC＝45°，AE⊥BC，连接BD分别交AE，AF于G，H，在不添加任何辅助线的情况下，直接写出图中所有的只含有一个3∠ABD的三角形．

查看试题解析
25. 在“抗击疫情”期间，某学校工会号召广大教师积极开展了“献爱心捐款”活动，学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品60件，B种物品45件，共需1140元；如果购买A种物品45件，B种物品30件，共需840元.

(1)、求A、B两种防疫物品每件各多少元；

(2)、现要购买A、B两种防疫物品共600件，总费用不超过7000元，那么A种防疫物品最多购买多少件？

查看试题解析
26. 如图，AB、CD都是⊙O的直径，连接AD，BC．

(1)、求证：AD＝BC；

(2)、过D点作⊙O的切线DE交BA的延长线于点E，F是BE上一点，连接CF交⊙O于点M，若ED＝CF，求证：∠BED＝∠CFB．

(3)、在（2）的条件下，连接DM交EB于点N，连接CN，若tan∠CNO＝ $\frac{2}{3}$ ，ON＝ $2 \sqrt{5}$ ，求DE的长．

查看试题解析
27. 已知抛物线 $y = a x^{2} + \frac{8}{3} x + 4$ 与x轴分别交于A，B两点，与y轴交于点C，直线BC的解析式： $y = - \frac{4}{3} x + n$ ；

(1)、求抛物线的解析式；

(2)、若P为第一象限抛物线上一点，PH⊥BC于H，线段PH的长为d，设P点的横坐标为t，求d与t的函数关系式，并直接写出t的取范围；

(3)、在（2）的条件下，连接PB，过P点作PE⊥x轴于E，AG⊥x轴，连接BG，PG，PE交BG于T，若∠ABG＝∠EPB，∠PGB＝45°+∠BPE，求P点坐标．

查看试题解析