黑龙江省大庆市龙凤区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-29 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、 B、 C、 D、2. 抛物线 的图像经过点 , , ,则 , , 大小关系是( )A、 B、 C、 D、3. 下列说法正确的是( )A、相等的圆心角所对的弧相等 B、平分弦的直径垂直弦并平分弦所对的弧 C、相等的弦所对的圆心角相等 D、等弧所对的弦相等4. 如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为( )
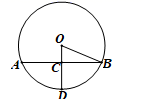 A、3 B、4 C、5 D、65. 在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是( )A、
A、3 B、4 C、5 D、65. 在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是( )A、 B、
B、 C、
C、 D、
D、 6. 在 中, , 为锐角,且有 ,则这个三角形是( )A、等腰三角形 B、直角三角形 C、钝角三角形 D、锐角三角形7. 已知关于 的二次函数 的图象与 轴交于 , 两点,且满足 , 的值( )A、 或 B、 或 C、 或 D、8. 如图, 中, 是 的直径, , , 是 上一动点, 的最小值是( )
6. 在 中, , 为锐角,且有 ,则这个三角形是( )A、等腰三角形 B、直角三角形 C、钝角三角形 D、锐角三角形7. 已知关于 的二次函数 的图象与 轴交于 , 两点,且满足 , 的值( )A、 或 B、 或 C、 或 D、8. 如图, 中, 是 的直径, , , 是 上一动点, 的最小值是( ) A、 B、 C、 D、9. 如图,已知圆锥的母线长为 ,底面半径为 ,则此圆锥侧面展开图的圆心角的度数是( )
A、 B、 C、 D、9. 如图,已知圆锥的母线长为 ,底面半径为 ,则此圆锥侧面展开图的圆心角的度数是( )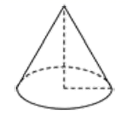 A、 B、 C、 D、10. 如图,有一圆形纸片圆心为 ,直径 的长为 , ,将纸片沿 、 折叠,交于点 ,那么阴影部分面积为( )
A、 B、 C、 D、10. 如图,有一圆形纸片圆心为 ,直径 的长为 , ,将纸片沿 、 折叠,交于点 ,那么阴影部分面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 是二次函数,则m=.12. 把抛物线 向左平移 个单位,然后向上平移 个单位,平移后抛物线的顶点坐标为 .13. 二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是 .14. 已知 的半径为 ,直线 与 相交,则圆心 到直线 距离 的取值范围是 .15. 如图,四边形 是 的外切四边形,且 , ,则四边形 的周长为 .
 16. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
16. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .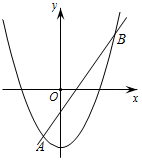 17. 如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
17. 如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 . 18. 如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 ,则 的度数是 .
18. 如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 ,则 的度数是 .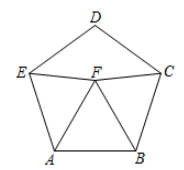 19. 如图,△ABC的内切圆的三个切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF=度.
19. 如图,△ABC的内切圆的三个切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF=度. 20. 如图,平行四边形 中, , , ,点 在边 上运动以 为圆心, 为半径作 ,若 与平行四边形 的边有四个公共点,则 的长度满足条件是 .
20. 如图,平行四边形 中, , , ,点 在边 上运动以 为圆心, 为半径作 ,若 与平行四边形 的边有四个公共点,则 的长度满足条件是 .
三、解答题
-
21. 计算:2sin 30°-3tan 45°·sin 45°+4cos 60°.22. 如图,正方形网格中有—段弧,弧上三点 , , 均在格点上.
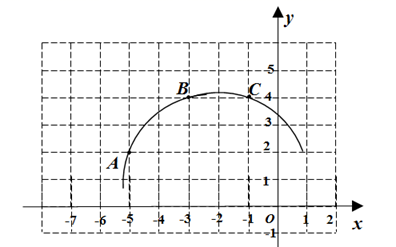 (1)、圆心 的坐标是(), .(2)、求 的长度.23. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35 m的速度沿着与水平方向成75°角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号).
(1)、圆心 的坐标是(), .(2)、求 的长度.23. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35 m的速度沿着与水平方向成75°角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号). 24. 已知二次函数 的图像与直线 交于点 、点 .(1)、求 的表达式和 的值;(2)、当 时,求自变量 的取值范围;(3)、将直线 沿 轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.25. 新冠疫情期间,某网店销售的消毒用紫外线灯很畅销,该网店店主结合店铺数据发现日销量 (件)是售价 (元/件)的一次函数,其售价、日销售量、日销售纯利润 (元)的四组对应值如表:
24. 已知二次函数 的图像与直线 交于点 、点 .(1)、求 的表达式和 的值;(2)、当 时,求自变量 的取值范围;(3)、将直线 沿 轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.25. 新冠疫情期间,某网店销售的消毒用紫外线灯很畅销,该网店店主结合店铺数据发现日销量 (件)是售价 (元/件)的一次函数,其售价、日销售量、日销售纯利润 (元)的四组对应值如表:售价 (元/件)
日销量 (件)
日销售纯利润 (元)
另外,该网店每日的固定成本折算下来为 元.
注:日销售纯利润=日销售灵 (售价-进价)-每日固定成本
(1)、该商品进价是元/件;(2)、求 关于 的函数解析式(不要求写出自变量的取值范围);(3)、当售价 (元/件)定为多少时,日销售纯利润 (元)最大,求出最大纯利润.26. 如图,在 中, , 、 的长恰好为方程 的两根,且 . (1)、求 的值.(2)、动点 从点 出发,沿 的路线向点 运动(不包括端点);点 从点 出发,沿 的路线向点C运动(不包括端点).若点 、 同时出发,速度都为每秒 个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为 秒,在整个运动过程中,设 的面积为 ,试求 与 之间的函数关系式;并指出自变量 的取值范围和 的范围.
(1)、求 的值.(2)、动点 从点 出发,沿 的路线向点 运动(不包括端点);点 从点 出发,沿 的路线向点C运动(不包括端点).若点 、 同时出发,速度都为每秒 个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为 秒,在整个运动过程中,设 的面积为 ,试求 与 之间的函数关系式;并指出自变量 的取值范围和 的范围.

