黑龙江省大庆市林甸县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-29 类型：期末考试

进入出卷网下载

一、单选题

1. 小亮、小莹、大刚三位同学随机地站成一排合影留念，小亮恰好站在中间的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

查看试题解析
2.
如图，在一间黑屋子里用一盏白炽灯照一个球，球在地面上的阴影的形状是一个圆，当把白炽灯向上远移时，圆形阴影的大小的变化情况是（　　）

A、越来越小 B、越来越大 C、大小不变 D、不能确定

查看试题解析
3. 桌上摆着一个由若干个相同的小正方体组成的几何体，其主视图和左视图如图所示，则组成这个几何体的小正方体的个数最多有（）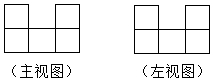

A、12个 B、8个 C、14个 D、13个

查看试题解析
4. 已知点A（x $_{1}$ ，y $_{1}$ ），B（x $_{2}$ ，y $_{2}$ ），C（x $_{3}^{}$ ，y $_{3}$ ）都在反比例函数y= $\frac{k}{x}$ （k<0）的图象上，且x $_{1}$ <x $_{2}$ <0<x $_{3}^{}$ ，则y $_{1}$ ，y $_{2}$ ，y $_{3}$ 的大小关系是（）

A、y $_{2}$ >y $_{1}$ >y $_{3}$ B、y $_{3}$ >y $_{2}$ >y $_{1}$ C、y $_{1}$ >y $_{2}$ >y $_{3}$ D、y $_{3}$ >y $_{1}$ >y $_{2}$

查看试题解析
5. 一元二次方程x²+bx﹣2=0中，若b＜0，则这个方程根的情况是（）

A、有两个正根 B、有一正根一负根且正根的绝对值大 C、有两个负根 D、有一正根一负根且负根的绝对值大

查看试题解析
6. 若关于 $x$ 的一元二次方程 $x^{2} + m x + m^{2} - 3 m + 3 = 0$ 的两根互为倒数，则 $m$ 的值等于（）

A、 $1$ B、 $2$ C、 $1$ 或 $2$ D、 $0$

查看试题解析
7. 已知一个菱形的周长是 $20 c m$ ，两条对角线的比是4：3，则这个菱形的面积是（）

A、 $12 c m^{2}$ B、 $24 c m^{2}$ C、 $48 c m^{2}$ D、 $96 c m^{2}$

查看试题解析
8. 若a+b=3，a－b=7，则 $b^{2} - a^{2}$ 的值为（）

A、－21 B、21 C、－10 D、10

查看试题解析
9. 如图所示的正方形网格中，网格的交点称为格点，已知 $A$ ， $B$ 是两格点，如果 $C$ 也是图中的格点，且使得 $Δ A B C$ 为等腰三角形，则符合条件的点 $C$ 的个数是（）

A、6 B、7 C、8 D、9

查看试题解析
10. 如图，在△ABC中，AC的垂直平分线交AB于点D，CD平分∠ACB，若∠A＝50°，则∠B的度数为（）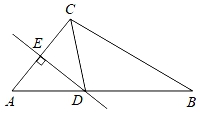

A、25° B、30° C、35° D、40°

查看试题解析

二、填空题

11. 一水库里有鲤鱼、鲫鱼、草鱼共2 000尾，小明通过多次捕捞试验，发现鲤鱼、草鱼的概率是51%和26%，则水库里有尾鲫鱼．

查看试题解析
12. 在某一时刻，测得一根高为 $1.8 m$ 的竹竿的影长为 $3 m$ ，同时同地测得一栋楼的影长为 $90 m$ ，则这栋楼的高度为 $m$ ．

查看试题解析
13. 已知函数 $y = (n + 1) x^{n^{2} - 2}$ 是反比例函数，则 $n$ 的值为．

查看试题解析
14. 当m=时，关于x的方程（m+2）x $^{m^{2} - 2}$ +5x+7=0是一元二次方程．

查看试题解析
15. 对于非零的两个实数a、b，规定a⊕b= $\frac{1}{b} - \frac{1}{a}$ ，若2⊕（2x﹣1）=1，则x的值为．

查看试题解析
16. 一个三角形三条边长分别为xcm、（x+1）cm、（x+2）cm，它的周长不超过39cm，则x的取值范围是．

查看试题解析
17. 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=5cm，BC=12cm，则EF= cm．

查看试题解析
18. 如图，在正方形 $A B C D$ ，E是对角线 $B D$ 上一点， $A E$ 的延长线交 $C D$ 于点F，连接 $C E$ ．若 $∠ B A E = 56 °$ ，则 $∠ C E F =$ $°$ ．

查看试题解析

三、解答题

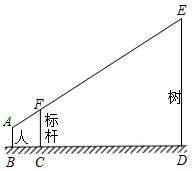
19. 解一元二次方程2（x-3） $^{2}$ =x $^{2}$ -9

查看试题解析
20. 为了测量校园内水平地面上的一棵树的高度，小明在距树5米处立了一根高为3米的标杆，然后小明前后调整自己的位置，当小明与标杆相距1米时，小明的眼睛A、标杆顶端F、树的顶端E在同一直线上．已知小明的眼睛距地面1.5米，求树的高度．

查看试题解析
21. 如图，已知∠BAC＝∠EAD，AB＝20.4，AC＝48，AE＝17，AD＝40．
求证：△ABC∽△AED．

查看试题解析
22. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E，若AC=8，BD=6，求BE的长．

查看试题解析
23. 今年我国发生了较为严重的新冠肺炎疫情，口罩供不应求．某商店恰好年前新进了一批口罩，若按每个盈利1元销售，每天可售出200个，如果每个口罩的售价上涨0.5元，则销售量就减少10件，问应将每件涨价多少元时，才能让顾客得到实惠的同时每天利润为480元？

查看试题解析
24. 如图，在△ABC中，∠B= $90^{0}$ ，AB=6cm，BC=8cm，点P从点A开始，以1cm/s的速度沿AB边向点B移动，点Q从点B开始以2cm/s的速度沿BC边向点C移动．如果点P，Q分别从点A，B同时出发，经过几秒钟，能使△PBQ的面积等于8 $c m^{2}$ ？

查看试题解析
25. 如图，矩形ABCD中，点P是线段AD上任意一点，点Q为BC上一点，且AP=CQ.

(1)、求证：BP=DQ；

(2)、若AB=4，且当PD=5时四边形PBQD为菱形.求AD为多少.

查看试题解析
26. 已知一艘轮船上装有100吨货物，轮船到达目的地后开始卸货，设平均卸货速度为v（单位：吨/小时），卸完这批货物所需的时间为t（单位：小时）。

(1)、求v关于t的函数表达式

(2)、若要求不超过5小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？

查看试题解析
27. 如图，在平面直角坐标系中，一次函数y=kx+b(k≠0)与反比例函数 $y = \frac{m}{x}$ (m≠0)的图象交于点A(3，1)，且过点B(0，-2).

(1)、求反比例函数和一次函数的表达式.

(2)、如果点P是x轴上位于直线AB右侧的一点，且ΔABP的面积是3，求点P的坐标.

查看试题解析
28. 如图，在 $△ A B C$ 中，点 $D ， E$ 分别在边 $A B ， A C$ 上， $D E ， B C$ 的延长线相交于点 $F$ ，且 $\frac{F E}{F B} = \frac{F C}{F D}$

(1)、求证： $△ A D E \sim △ A C B ；$

(2)、当 $A B = 12 ， A C = 9 ， A E = 8$ 时，求 $B D$ 的长

查看试题解析