河南省信阳市罗山县2020-2021学年高三上学期理数第二次调研考试试卷

试卷更新日期：2021-09-29 类型：月考试卷

进入出卷网下载

一、单选题

1. 若集合 $M = {x | x^{2} - 3 x = 0}$ ， $N = {x | \log_{2} x < 2}$ ，则 $M \cup N =$ （）

A、{-2} B、 $(0 ， 4)$ C、 $(- \infty ， 4)$ D、 $[0 ， 4)$

查看试题解析
2. 已知复数 $z$ 满足 $(2 - i) z = 1 + 2 i$ （ $i$ 为虚数单位），则 $z$ 的虚部为（）

A、1 B、-1 C、0 D、 $i$

查看试题解析
3. 有下列四个命题： $p_{1}$ ： $\forall x \in R$ ， $sin x \leq 1$ . $p_{2}$ ： $\exists n \in N$ ， $n^{2} > 2^{n}$ . $p_{3}$ ： $a + b = 0$ 的充要条件是 $\frac{a}{b} = - 1$ . $p_{4}$ ：若 $p \lor q$ 是真命题，则 $p$ 一定是真命题.其中真命题是（）

A、 $p_{1}$ ， $p_{2}$ B、 $p_{2}$ ， $p_{3}$ C、 $p_{3}$ ， $p_{4}$ D、 $p_{1}$ ， $p_{4}$

查看试题解析
4. 函数 $f (x) = (2^{x} - 2^{- x}) \sin x \cos x$ 的部分图象大致是（）

A、 B、 C、 D、

查看试题解析
5. 设函数 $f (x) = sin (\frac{1}{2} x + θ) - \sqrt{3} cos (\frac{1}{2} x + θ) (| θ | < \frac{π}{2})$ 的图像关于原点对称，则 $θ$ 的值为（）

A、 $- \frac{π}{6}$ B、 $\frac{π}{6}$ C、 $- \frac{π}{3}$ D、 $\frac{π}{3}$

查看试题解析
6. 中国的5G技术领先世界，5G技术的数学原理之一便是著名的香农公式： $C = W \log_{2} (1 + \frac{S}{N})$ .它表示：在受噪声干扰的信道中，最大信息传递速度 $C$ 取决于信道带宽 $W$ ，信道内信号的平均功率 $S$ ，信道内部的高斯噪声功率 $N$ 的大小，其中 $\frac{S}{N}$ 叫做信噪比.当信噪比比较大时，公式中真数中的1可以忽略不计.按照香农公式，若不改变带宽 $W$ ，而将信噪比 $\frac{S}{N}$ 从1000提升至4000，则 $C$ 大约增加了（）附： $\lg 2 \approx 0.3010$

A、10% B、20% C、50% D、100%

查看试题解析
7. 一个蜂巢里有1只蜜蜂，第1天，它飞出去找回了3个伙伴；第2天，4只蜜蜂飞出去，各自找回了3个伙伴......如果这个找伙伴的过程继续下去，第6天所有的蜜蜂都归巢后，蜂巢中蜜蜂的总只数为（）

A、243 B、729 C、1024 D、4096

查看试题解析
8. 下列说法正确的是（）
①在残差图中，残差点比较均匀地落在水平带状区域中，说明选用的模型比较合适，带状区域越窄，说明回归方程的预报精度越高；②在独立性检验时，两个变量的 $2 \times 2$ 列联表中，对角线上数据的乘积相差越大，说明“这两个变量没有关系”成立的可能性就越大；③在回归直线方程 $\hat{y} = 0.2 x + 12$ 中，当解释变量 $x$ 每增加一个单位时，预报变量 $\hat{y}$ 就增加0.2个单位；④ $R^{2}$ 越大，意味着残差平方和越小，即模型的拟合效果越好.

A、①②③ B、②③ C、①④ D、①③④

查看试题解析
9. 执行下面的程序框图，若输出的 $S$ 的值为63，则判断框中可以填入的关于 $i$ 的判断条件是（）

A、 $i \leq 5$ B、 $i \leq 6$ C、 $i \leq 7$ D、 $i \leq 8$

查看试题解析
10. 设 $f (x)$ 是定义在 $R$ 上的偶函数，且 $f (2 + x) = f (2 - x)$ ，当 $x \in [- 2 ， 0]$ 时， $f (x) = {(\frac{\sqrt{2}}{2})}^{x} - 1$ ，若关于 $x$ 的方程 $f (x) - \log_{a} (x + 2) = 0 (a > 0 ， a \neq 1)$ 在区间 $(- 2 ， 10)$ 内恰有5个不同的实数根，则实数 $a$ 的取值范围是（）

A、 $(8 ， 12)$ B、 $(12 ， + \infty)$ C、 $(8 ， 12]$ D、 $(1 ， 8)$

查看试题解析
11. 已知点 $G$ 是 $Δ A B C$ 的重心， $\overset{⇀}{A G} = λ \overset{⇀}{A B} + μ \overset{⇀}{A C} (λ ， μ \in R)$ ，若 $∠ A = 120^{\circ}$ ， $\overset{⇀}{A B} \cdot \overset{⇀}{A C} = - 2$ ，则 $| \overset{⇀}{A G} |$ 的最小值是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
12. 已知函数 $f (x) = \sin ω x + a \cos ω x$ ，周期 $T < 2 π$ ， $f (\frac{π}{3}) = \sqrt{3}$ ，且在 $x = \frac{π}{6}$ 处取得最大值，则使得不等式 $λ | ω | \geq a$ 恒成立的实数 $λ$ 的最小值为（）

A、 $\frac{\sqrt{3}}{10}$ B、 $\frac{\sqrt{3}}{11}$ C、 $\frac{\sqrt{3}}{12}$ D、 $\frac{\sqrt{3}}{13}$

查看试题解析

二、填空题

13. 已知实数 $x ， y$ 满足不等式组 ${\begin{array}{l} 2 x - y \leq 0 \\ x + y - 3 \geq 0 \\ x + 2 y \leq 6 \end{array}$ ，则 $z = | x - 2 y |$ 的最小值为．

查看试题解析
14. 若非零向量 $a$ ， $b$ 满足 $〈 \overset{⇀}{a}, \overset{⇀}{b} 〉 = \frac{π}{6}$ ， $| \overset{⇀}{a} | = \sqrt{3}$ ， $| \overset{⇀}{a} + 2 \overset{⇀}{b} | = \sqrt{7}$ ，则 $| \overset{⇀}{b} | =$ .

查看试题解析
15. 现有5人参加抽奖活动，每人依次从装有5张奖票（其中3张为中奖票）的箱子中不放回地随机抽取一张，直到3张中奖票都被抽出时活动结束，则活动恰好在第4人抽完后结束的概率为．

查看试题解析
16. 设 $S_{n}$ 是数列 ${a_{n}}$ 的前 $n$ 项和， $a_{1} = 3$ ，当 $n \geq 2$ 时有 $S_{n} + S_{n - 1} - 2 S_{n} S_{n - 1} = 2 n a_{n}$ ，则使 $S_{1} S_{2} \dots S_{m} \geq 2021$ 成立的正整数 $m$ 的最小值为.

查看试题解析

三、解答题

17. 已知函数 $f (x) = x^{2} + 2 x$ ， $g (x) = | x - 1 | - | x + 3 |$ .

(1)、求不等式 $g (x) \leq 3$ 的解集；

(2)、若关于 $x$ 的不等式 $f (m) + m \leq g (x)$ 的解集非空，求 $m$ 的取值范围.

查看试题解析
18. 在 $Δ A B C$ 中，三边 $a$ ， $b$ ， $c$ 的对角分别为 $A$ ， $B$ ， $C$ ，已知 $a = 3$ ， $\frac{\cos B + \cos A \cos C}{\sin B \cos C} = \frac{\sqrt{3} a}{b}$ .

(1)、若 $c = 2 \sqrt{3}$ ，求 $\sin A$ ；

(2)、若 $A B$ 边上的中线长为 $\frac{\sqrt{37}}{2}$ ，求 $Δ A B C$ 的面积.

查看试题解析
19. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 2, S_{n + 1} = 3 S_{n} + 2, n \in N^{*}$ .

(1)、证明：数列 ${S_{n} + 1}$ 为等比数列；

(2)、若 $b_{n} = {\begin{array}{l} \frac{a_{n}}{2}, n 为奇数 \\ {log}_{3} \frac{3 a_{n}}{2}, n 为偶数 \end{array}$ ，求数列 ${b_{n}}$ 的前 $2 n$ 项的和 $T_{2 n}$ .

查看试题解析

20. 为响应党中央“扶贫攻坚”的号召，某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高，根据以往的经验，随着温度的升高，其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数：

温度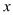（单位：℃）	21	23	24	27	29	32
死亡数y（单位：株）	6	11	20	27	57	77

经计算： $\bar{x} = \frac{1}{6} \sum_{i = 1}^{6} x_{i} = 26$ ， $\bar{y} = \frac{1}{6} \sum_{i = 1}^{6} y_{i} = 33$ ， $\sum_{i = 1}^{6} (x_{i} - \bar{x}) (y_{i} - \bar{y}) = 557$ ， $\sum_{i = 1}^{6} {(x_{i} - \bar{x})}^{2} = 84$ ， $\sum_{i = 1}^{6} {(y_{i} - \bar{y})}^{2} = 3930$ ， $\sum_{i = 1}^{6} {(y_{i} - \hat{y})}^{2} = 236.64$ ， $e^{8.065} \approx 3167$ ，其中 $x_{i}$ ， $y_{i}$ 分别为试验数据中的温度和死亡株数， $i = 1 ， 2 ， 3 ， 4 ， 5 ， 6$ .

附：对于一组数据 $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ ，……， $(u_{n} ， v_{n})$ ，其回归直线 $\hat{v} = \hat{α} + \hat{β} u$ 的斜率和截距的最小二乘估计分别为： $\hat{β} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}}$ ， $\hat{a} = \bar{v} - \hat{β} \bar{u}$ ；相关指数为： $R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(v_{i} - {\hat{v}}_{i})}^{2}}{\sum_{i = 1}^{n} {(v_{i} - {\bar{v}}_{i})}^{2}}$ .

(1)、若用线性回归模型，求

y

关于

x

的回归方程

\hat{y} = \hat{b} x + \hat{a}

（结果精确到0.1）；

(2)、若用非线性回归模型求得

y

关于

x

的回归方程

\hat{y} = 0.06 e^{0.2303 x}

，且相关指数为

R^{2} = 0.9522

（i）试与（1）中的回归模型相比，用 $R^{2}$ 说明哪种模型的拟合效果更好；

（ii）用拟合效果好的模型预测温度为 $35^{°} C$ 时该紫甘薯死亡株数（结果取整数）.

查看试题解析

21. 已知函数 $f (x) = a x^{2} - x - \ln \frac{1}{x}$ ．

(1)、若 $f (x)$ 在点 $(1 ， f (1))$ 处的切线与直线 $y = 2 x ＋ 1$ 平行，求 $f (x)$ 在点 $(1 ， f (1))$ 的切线方程；

(2)、若函数 $f (x)$ 在定义域内有两个极值点 $x_{1}$ ， $x_{2}$ ，求 $a$ 的取值范围，并求证： $f (x_{1}) + f (x_{2}) < 2 \ln 2 - 3$ ．

查看试题解析
22. 已知函数 $f (x) = (x - \frac{1}{2}) e^{x} + a {(x + \frac{1}{2})}^{2} .$

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 有两个零点，求 $a$ 的取值范围.

查看试题解析