河北省张家口市2021届高三上学期数学12月阶段测试试卷
试卷更新日期:2021-09-29 类型:月考试卷
一、单选题
-
1. 设集合 , ,则( )A、 B、 C、 D、2. 已知数列 , , 均为等差数列,且 , ,则 ( )A、4037 B、4039 C、4041 D、40433. 若 ,则( )A、 B、 C、 D、4. 在 中,内角 , , 所对的边分别为 , , ,若 的面积为 .且 ,则 ( )A、 B、 C、 D、5. 某几何体的三视图如图所示,则该几何体的体积是( )
 A、 B、2π C、 D、6. 图1是第七届国际数学教育大会( )的会徽图案,它是由一串直角三角形演化而成的(如图2),其中 ,则 ( )
A、 B、2π C、 D、6. 图1是第七届国际数学教育大会( )的会徽图案,它是由一串直角三角形演化而成的(如图2),其中 ,则 ( )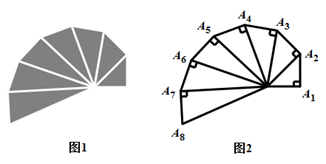 A、 B、 C、 D、7. 在三棱柱 ,底面 为等边三角形,侧面 是菱形,且 ,侧面 底面 ,点 是 的中点,则直线 与平面 所成的角为( )A、 B、 C、 D、8. 设 是定义在 上的函数, 为其导函数,已知 , ,当 时, ,则使得 成立的 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、7. 在三棱柱 ,底面 为等边三角形,侧面 是菱形,且 ,侧面 底面 ,点 是 的中点,则直线 与平面 所成的角为( )A、 B、 C、 D、8. 设 是定义在 上的函数, 为其导函数,已知 , ,当 时, ,则使得 成立的 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 若命题“ , ”是假命题,则 的值可能为( )A、-1 B、1 C、4 D、710. 将函数 的图像向左平移 个单位长度,得到 的图像,则( )A、 在 上是减函数 B、 C、 是奇函数 D、 在 上有4个零点11. 在长方体 中, , ,点 在线段 上, 为 的中点,则( )A、 平面 B、当 为 的中点时,四棱锥 外接球半径为 C、三棱锥 体积为定值 D、过点 作长方体 的外接球截面,所得截面圆的面积的最小值为12. 已知函数 的定义域为 , 为自然底数,给出下列结论:① 是奇函数;② 是 上的增函数;③ 在 上的值域是 ;④ 在 上有实根,其中正确的结论是( )A、① B、② C、③ D、④
三、填空题
-
13. 已知集合 , ,若 ,则实数 的取值范围是 .14. 在四面体 中, , , ,则点 到平面 的距离是.15. 已知正数 , 满足 ,则 的最小值为.16. 在 中,内角 , , 所对的边分别为 , , , ,则 外接圆面积的最小值为.
四、解答题
-
17. 在① ,② , 为 的中点,③ , 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求 的长;若问题中的三角形不存在,说明理由.
问题:是否存在 ,在 中, ,点 在线段 上, , ▲ ?
注:如果选择多个条件分别解答,按第一个解答计分.
18. 已知 是各项均为正数的等比数列, 为 , 的等差中项.且 .(1)、求 的通项公式;(2)、设 ,求 的前 项和.19. 已知函数 .(1)、求函数 的最小正周期 及 的值;(2)、若关于 的方程 ,在 上有3个解,求实数 的取值范围.

