安徽省淮北市2021届高三理数一模试卷
试卷更新日期:2021-09-29 类型:高考模拟
一、单选题
-
1. 已知集合U={−2,−1,0,1,2,3},A={−1,0,1},B={1,2},则 ( )A、{−2,3} B、{−2,2,3} C、{−2,−1,0,3} D、{−2,−1,0,2,3}2. 若数列 为等差数列,且 , ,则 ( )A、 B、 C、 D、3. 函数 的部分图象大致形状是( )A、
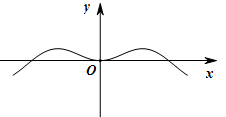 B、
B、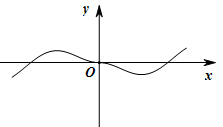 C、
C、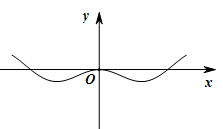 D、
D、 4. 已知平面 , ,直线l,m,且有 , ,给出下列命题:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,则 .其中正确命题的个数是( )A、1 B、2 C、3 D、45. 在 中,点D是线段 (不包括端点)上的动点,若 ,则( )A、 B、 C、 D、6. 某地气象局把当地某月(共30天)每一天的最低气温作了统计,并绘制了如下图所示的统计图.记这组数据的众数为M,中位数为N,平均数为P,则( )
4. 已知平面 , ,直线l,m,且有 , ,给出下列命题:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,则 .其中正确命题的个数是( )A、1 B、2 C、3 D、45. 在 中,点D是线段 (不包括端点)上的动点,若 ,则( )A、 B、 C、 D、6. 某地气象局把当地某月(共30天)每一天的最低气温作了统计,并绘制了如下图所示的统计图.记这组数据的众数为M,中位数为N,平均数为P,则( ) A、 B、 C、 D、7. 若i为虚数单位,复数z满足 ,则 的最大值为( )A、2 B、3 C、 D、8. 甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上,各人帽子的颜色互不相同,乙比戴蓝帽的人年龄大,丙和戴红帽的人年龄不同,戴红帽的人比甲年龄小,则甲、乙、丙所戴帽子的颜色分别为( )A、红、黄、蓝 B、黄、红、蓝 C、蓝、红、黄 D、蓝、黄、红9. 过圆 上的动点作圆 的两条切线,两个切点之间的线段称为切点弦,则圆 内不在任何切点弦上的点形成的区域的面积为( )A、π B、 C、2π D、3π10. 已知函数 ,则函数 零点的个数为( )A、3 B、4 C、5 D、611. 已知双曲线 的左焦点为F,左顶点为A,直线 交双曲线于P、Q两点(P在第一象限),直线 与线段 交于点B,若 ,则该双曲线的离心率为( )A、2 B、3 C、4 D、512. 函数 的最大值为( )A、 B、 C、 D、3
A、 B、 C、 D、7. 若i为虚数单位,复数z满足 ,则 的最大值为( )A、2 B、3 C、 D、8. 甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上,各人帽子的颜色互不相同,乙比戴蓝帽的人年龄大,丙和戴红帽的人年龄不同,戴红帽的人比甲年龄小,则甲、乙、丙所戴帽子的颜色分别为( )A、红、黄、蓝 B、黄、红、蓝 C、蓝、红、黄 D、蓝、黄、红9. 过圆 上的动点作圆 的两条切线,两个切点之间的线段称为切点弦,则圆 内不在任何切点弦上的点形成的区域的面积为( )A、π B、 C、2π D、3π10. 已知函数 ,则函数 零点的个数为( )A、3 B、4 C、5 D、611. 已知双曲线 的左焦点为F,左顶点为A,直线 交双曲线于P、Q两点(P在第一象限),直线 与线段 交于点B,若 ,则该双曲线的离心率为( )A、2 B、3 C、4 D、512. 函数 的最大值为( )A、 B、 C、 D、3二、填空题
-
13. 若x,y满足约束条件 ,则 的最大值为.14. 二项式 的展开式中的常数项为 .15. 已知数列 的前n项和为 ,且 ,若 ,则数列 的前 项和为.16. 在棱长为 的正方体 中, 是 的中点, 是 上的动点,则三棱锥 外接球表面积的最小值为.
三、解答题
-
17. 在 中,内角A,B,C所对的边分别为a,b,c,且 .(1)、求角B的大小;(2)、若 , ,求 的面积18. 如图,在多面体 中,四边形 是边长为 的正方形, , ,且 , , 面 , ,N为 中点.
 (1)、若 是 中点,求证: 面 ;(2)、求二面角 的正弦值.19. 甲、乙两人进行乒乓球比赛,规定比赛进行到有一人比对方多赢2局或打满6局时比赛结束.设甲、乙在每局比赛中获胜的概率均为 ,各局比赛相互独立,用X表示比赛结束时的比赛局数(1)、求比赛结束时甲只获胜一局的概率;(2)、求X的分布列和数学期望.20. 已知函数 , .(1)、若 是增函数,求实数m的取值范围;(2)、当 时,求证: .21. 已知椭圆 的离心率为 ,左顶点为A,右焦点F, .过F且斜率存在的直线交椭圆于P,N两点,P关于原点的对称点为M.(1)、求椭圆C的方程;(2)、设直线 , 的斜率分别为 , ,是否存在常数 ,使得 恒成立?若存在,请求出 的值,若不存在,请说明理由.
(1)、若 是 中点,求证: 面 ;(2)、求二面角 的正弦值.19. 甲、乙两人进行乒乓球比赛,规定比赛进行到有一人比对方多赢2局或打满6局时比赛结束.设甲、乙在每局比赛中获胜的概率均为 ,各局比赛相互独立,用X表示比赛结束时的比赛局数(1)、求比赛结束时甲只获胜一局的概率;(2)、求X的分布列和数学期望.20. 已知函数 , .(1)、若 是增函数,求实数m的取值范围;(2)、当 时,求证: .21. 已知椭圆 的离心率为 ,左顶点为A,右焦点F, .过F且斜率存在的直线交椭圆于P,N两点,P关于原点的对称点为M.(1)、求椭圆C的方程;(2)、设直线 , 的斜率分别为 , ,是否存在常数 ,使得 恒成立?若存在,请求出 的值,若不存在,请说明理由.