重庆市璧山区八校2020-2021学年七年级上学期数学期中联考试卷

试卷更新日期：2021-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $0, - 1, - 2, - 3, 53, 8, - 1 \frac{2}{5}, \frac{1}{6}$ 这8个有理数中，负数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 如果向左走3米记作+3米，那么向右走了5米可以记作（）

A、+3米 B、-3米 C、+5米 D、-5米

查看试题解析
3. 下列等式是一元一次方程的是（）

A、 $s = a + b$ B、 $2 - 5 = - 3$ C、 $\frac{x}{2} + 1 = - x - 2$ D、3x+2y＝5

查看试题解析
4. 下列说法正确的是（）

A、有理数都可以用数轴上的点表示 B、数轴上的点都表示有理数 C、在数轴上离原点越远，所表示的有理数越大 D、在数轴上离原点越近，所表示的有理数越小

查看试题解析
5. 单项式 $- \frac{a^{2} b^{3}}{3}$ 的系数和次数是（）

A、系数是 $\frac{1}{3}$ ，次数是 $3$ B、系数是 $- \frac{1}{3}$ ，次数是 $5$ C、系数是 $- \frac{1}{3}$ ，次数是 $3$ D、系数是 $5$ ，次数是 $- \frac{1}{3}$

查看试题解析
6. 下列运算正确的是（） .

A、 $- 2 + (- 5) = - (5 - 2) = - 3$ B、 $(+ 3) + (- 8) = - (8 - 3) = - 5$ C、 $(- 9) - (- 2) = - (9 + 2) = - 11$ D、 $(+ 6) + (- 4) = + (6 + 4) = + 10$

查看试题解析
7. 对于任意有理数 $a$ 和 $b$ ，规定 $a * b = a b^{2} + 2 a b + a$ .如 $1 * 3 = 1 \times 3^{2} + 2 \times 1 \times 3 + 1 = 16$ .则 $(- 4) * 2$ 的值为（）

A、36 B、-36 C、-8 D、-4

查看试题解析
8. 已知 $2 x - 3 y = 6$ ，则 $7 - 6 x + 9 y$ 的值为（）

A、25 B、-25 C、11 D、-11

查看试题解析
9. a、b是有理数，下列各式中成立的是（）

A、若 $a \neq b$ ，则 $| a | \neq | b |$ B、若 $| a | \neq | b |$ ，则 $a \neq b$ C、若 $a > b$ ，则 $| a | > | b |$ D、若 $| a | > | b |$ ，则 $a > b$

查看试题解析
10. 《九章算术》记载了这样一道题：“以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺，问绳长井深各几何？”题意是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺：如果将绳子折成四等份，那么每等份井外余绳一尺.问绳长和井深各多少尺？假设井深为x尺，则符合题意的方程应为（）

A、 $\frac{1}{3} x - 4 = \frac{1}{4} x - 1$ B、3x+4＝4x+1 C、 $\frac{1}{3} x + 4 = \frac{1}{4} x + 1$ D、3（x+4）＝4（x+1）

查看试题解析
11. $| x | = 17$ ， $| y | = 13$ ， $x < y$ ，则 $| x - y |$ 的值为（）

A、4 B、30 C、4或30 D、4或0

查看试题解析
12. 下面是用黑色棋子摆成的美丽图案，按照这样的规律摆下去，第10个这样的图案需要黑色棋子的个数为（）

A、148 B、152 C、174 D、202

查看试题解析

二、填空题

13. 数－2020的绝对值是．

查看试题解析
14. 璧山区现有耕地面积约为392000亩，将数据392000用科学记数法可表示为.

查看试题解析
15. 已知 $2 x^{3} y^{m}$ 与 $- x^{3 n} y^{2}$ 的和仍是单项式，则式子 $n - m$ ＝.

查看试题解析
16. 若 $a$ 、 $b$ 互为相反数， $c$ 、 $d$ 互为倒数，且 $| m | = 3$ ，则 ${(a + b)}^{2} + 2 c d + 2 m^{2} - m$ 的值为.

查看试题解析
17. 当 $a =$ 时，方程 $\frac{a x - 1}{3} + \frac{x + a}{2} = 1$ 解是 $x = 1$ ？

查看试题解析
18. 按照下面的程序计算：

如果输入 $x$ 的值是正整数，输出结果是166，那么满足条件的 $x$ 的值为.

查看试题解析

三、解答题

19. 计算：

(1)、 $(- \frac{1}{3}) - (- 3 \frac{1}{6}) - (+ 2 \frac{2}{3}) + (- 6 \frac{1}{6})$ ；

(2)、 $(- 8) \div \frac{2}{3} \times (- 1 \frac{1}{2}) \div (- 9)$ .

查看试题解析
20. 解方程：

(1)、 $2 x - (x - 3) = 3$ ；

(2)、 $\frac{7 x - 1}{3} - \frac{5 x + 1}{2} = 2 - \frac{3 x + 2}{4}$ .

查看试题解析

21. 璧山枫香湖儿童公园享誉重庆，今年“十一”黄金周期间，外地游客纷纷前来旅游打卡. 据统计，在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）.

日期

1日

2日

3日

4日

5日

6日

7日

人数变化

（单位：万人）

1.6

0.4

-1

-0.82

-2.4

-1.2

已知9月30日的游客人数为1万人，请回答下列问题.

(1)、七天内游客人数哪天最多？哪天最少？分别是多少？它们相差多少万人？

(2)、求这

7

天平均每天的游客人数是多少万人.

查看试题解析

22. 先化简，再求值： $- 3 (x^{2} y - \frac{1}{3} x y^{2}) - (- 3 x^{2} y + 2 x y^{2}) + x y$ ，其中 $x = 2$ ， $y = - \frac{1}{2}$ .

查看试题解析
23. 有理数 $a$ 、 $b$ 、 $c$ 在数轴上的位置如图：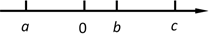

(1)、判断正负，用“>”或“<”填空： $b$ －c0， $a$ ＋ $b$ 0，c－ $a$ 0.

(2)、化简：| b－c|＋| $a$ ＋b|－|c－a|

查看试题解析
24. 已知多项式 $(2 x^{2} + a x - y + 6) - (2 b x^{2} - 3 x + 5 y - 1)$ .

(1)、若多项式的值与字母 $x$ 的取值无关，求 $a$ ， $b$ 的值；

(2)、在（1）的条件下，先化简多项式 $3 (a^{2} - a b + b^{2}) - (3 a^{2} + a b + b^{2})$ ，再求它的值.

查看试题解析
25. 式子“ $1 + 2 + 3 + 4 + \dots \dots + 100$ ”表示从 $1$ 开始的100个连续自然数的和，由于上述式子比较长，书写极不方便，为了简便，我们可以将“ $1 + 2 + 3 + 4 + \dots \dots + 100$ ”表示为“ $\sum_{n = 1}^{100} n$ ”，“ $\sum_{}^{}$ ”是求和的符号.例如： $\sum_{n = 1}^{50} (2 n - 1) = 1 + 3 + 5 + 7 + \dots \dots + 99$ ，又如： $\sum_{n = 1}^{10} n^{2} = 1^{2} + 2^{2} + 3^{2} + 4^{2} + \dots \dots + 10^{2}$ .通过对以上材料的阅读，请解答下列问题：

(1)、 $\sum_{n = 1}^{10} n =$ .

(2)、计算 $\sum_{n = 1}^{20} (4 n - 3)$ 的值.

查看试题解析
26. 如图，已知数轴上 $A$ 点表示数 $a$ ， $B$ 点表示数 $b$ ， $C$ 点表示数 $c$ .

(1)、当数 $a$ 、 $c$ 满足 $| a + 4 | + {(c - 8)}^{2} = 0$ 时，a= ， $c =$ .

(2)、若点 $P$ 为数轴上一动点，其对应的数为 $x$ ，认真观察图形并结合（1）的条件发现，随着点 $P$ 在数轴上左右移动，代数式 $| x - a | + | x - c |$ 可以取得最小值，这个最小值为.

(3)、结合图形及条件（1）可知点 $A$ 与点 $C$ 之间的距离可表示为 $A C = | a - c |$ ，同样，点 $A$ 与点 $B$ 之间的距离可表示为 $A B = | a - b |$ ，点 $B$ 与点 $C$ 之间的距离表示为 $B C = | b - c |$ ，若点 $B$ 在直线 $A C$ 上，且满足 $B C = A B$ ，求 $b$ 的值.

查看试题解析