河南省驻马店市驿城区2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. 25的平方根是（　　）

A、 ±5 B、5 C、± $\sqrt{5}$ D、﹣5

查看试题解析
2. 在下列各数中是无理数的个数有（）
－0.333…， $\sqrt{4}$ ， $\sqrt{5}$ ， -π， 3π， 3.1415， 2.010101…(相邻两个1之间有1个0)，76.0123456…(小数部分由相继的正整数组成).

A、3个 B、4个 C、5个 D、6个

查看试题解析
3. 下列说法错误的是（）

A、1的平方根是1 B、 $- 1$ 的立方根是 $- 1$ C、 $\sqrt{2}$ 是2的平方根 D、 $- \sqrt{3}$ 是 $\sqrt{{(- \sqrt{3})}^{2}}$ 的平方根

查看试题解析
4. 以下列各组数为边的三角形中，是直角三角形的有（）
（1）3，4，5；（2） $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ ；（3）3² ， 4² ， 5²；（4）0.03，0.04，0.05．

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若一次函数 $y = (m - 1) x + m^{2} - 1$ 的图象通过原点，则m的值为（）

A、 $m = - 1$ B、 $m = 1$ C、 $m = \pm 1$ D、 $m \neq 1$

查看试题解析
6. 一次函数y=kx+b，当k<0，b<0时，它的图象大致为（）

A、 B、 C、 D、

查看试题解析
7. 当 $\sqrt{4 a + 1}$ 的值为最小值时，a的取值为（）

A、 $- 1$ B、0 C、 $- \frac{1}{4}$ D、1

查看试题解析
8. 已知点M到x轴的距离为1，到y轴的距离为2，则M点的坐标为（）

A、(1，2) B、(－1，－2) C、(1，－2) D、(2，1)，(2，－1)，(－2，1)，(－2，－1)

查看试题解析
9. 平面直角坐标系中，点A(m ，－2）、B(1，n－m)关于x轴对称，则m、n的值为（）

A、m =1 ，n=1 B、m =－1 ，n=1 C、m =1 ，n=3 D、m =－1 ，n=3

查看试题解析
10. △ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（　　　）

A、42 B、32 C、42 或 32 D、37 或 33

查看试题解析

二、填空题

11. 36的平方根是； $\sqrt{16}$ 的算术平方根是.

查看试题解析
12. 在直角三角形ABC中，斜边AB=2，则AB²+AC²+BC²= ．

查看试题解析
13. 已知某一次函数的图象经过点 $A (0 ， 2)$ ， $B (1 ， 3)$ ， $C (a ， 1)$ 三点，则a的值是.

查看试题解析
14. 一次函数 $y = - 3 x + 6$ 的图象与x轴交点坐标是，与y轴交点坐标是，图象与坐标轴所围成的三角形面积是.

查看试题解析
15. 如图，在平面直角坐标系中有一个等边 $△ O B A$ ，其中A点坐标为 $(1 ， 0)$ ，将 $△ O B A$ 绕顶点A顺时针旋转 $120 °$ ，得到 $△ A O_{1} B_{1}$ ；将得到的 $△ A O_{1} B_{1}$ 绕顶点B₁顺时针旋转 $120 °$ ，得到 $△ B_{1} A_{1} O_{2}$ ；然后再将得到的 $△ B_{1} A_{1} O_{2}$ 绕顶点 $O_{2}$ 顺时针旋转 $120 °$ ，得到 $△ O_{2} B_{2} A_{2}$ …按照此规律，继续旋转下去，则 $A_{2014}$ 点的坐标为.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{8} + \sqrt{32} - \sqrt{2}$ ；

(2)、 $\sqrt{18} - {(\sqrt{2} + 1)}^{2} + (\sqrt{3} + 1) (\sqrt{3} - 1)$ .

查看试题解析
17. △ABC在直角坐标系内的位置如图所示．

(1)、在这个坐标系内画出△A₁B₁C₁ ，使△A₁B₁C₁与△ABC关于y轴对称；

(2)、求△ABC的面积．

查看试题解析
18. 学校要征收一块土地，形状如图所示，∠B=∠D=90°，AB=20m，BC=15m，CD=7m，土地价格为1 000元/m² ，请你计算学校征收这块地需要多少钱？

查看试题解析
19. 如图，某沿海开放城市A接到台风警报，在该市正南方向100km的B处有一台风中心，沿BC方向以20km/h的速度向D移动，已知城市A到BC的距离AD=60km，那么台风中心经过多长时间从B点移到D点？如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险，正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？

查看试题解析
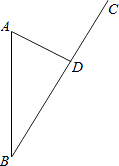20. 如图，已知在△ABC中，CD⊥AB于点D，BD＝9，BC＝15，AC＝20.

(1)、求CD的长；

(2)、求AB的长；

(3)、判断△ABC的形状．

查看试题解析
21. 已知一次函数 $y = k x + b$ 的图象经过点 $A (0 ， 2)$ 和点 $B (- a ， 3)$ ，且点B在正比例函数 $y = - 3 x$ 的图象上.

(1)、求a的值；

(2)、求一次函数的解析式；

(3)、若 $P (m ， y_{1})$ ， $Q (m - 1 ， y_{2})$ 是这个一次函数图象上的两点，试比较 $y_{1}$ 与 $y_{2}$ 的大小.

查看试题解析
22. 阅读下列材料，然后解答下列问题：
在进行代数式化简时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：

(一) $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ ；

(二) $\frac{2}{\sqrt{3} + 1} = \frac{2 （ \sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \sqrt{3} - 1$ ；

(三) $\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$ .

以上这种化简的方法叫分母有理化.

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ：
①参照(二)式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝_▲_.

②参照(三)式化简c＝_▲_

(2)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots + \frac{1}{\sqrt{99} + \sqrt{97}}$ .

查看试题解析
23. 如图所示，直线l₁的表达式为y=-3x+3，且与x轴交于点D，直线l₂经过点A、B，两直线交于点C.

(1)、求点D的坐标；

(2)、求直线l₂的解析式；

(3)、求△ADC的面积；

(4)、在直线l₂上存在异于点C的另一点P，使得△ADP和△ADC和面积相等.请直接写出点P的坐标.

查看试题解析