河南省驻马店市上蔡县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. 9的算术平方根是（）

A、 $\pm 3$ B、 $\pm \sqrt{9}$ C、3 D、-3

查看试题解析
2. 下列运算正确的是（）

A、 ${(a - 3)}^{2} = a^{2} - 9$ B、 $a^{2} + a^{5} = a^{10}$ C、 $\sqrt[3]{- 8} = - 2$ D、 $2 a + 3 a = 5 a^{2}$

查看试题解析
3. 一个正方形的面积是15，它的边长在两个相邻整数之间，则这两个整数是（）

A、1和2 B、2和3 C、3和4 D、4和5

查看试题解析
4. 下列多项式中，不能用平方差公式计算的是（）

A、 $(x + y) (- x - y)$ B、 $(- 2 a - 3 b) (- 2 a + 3 b)$ C、 $(b + 2 a) (2 a - b)$ D、 $(- 2 x - y) (2 x - y)$

查看试题解析
5. 多项式 $m x^{2} - m$ 与多项式 $x^{2} - 2 x + 1$ 的公因式是（）

A、 $x - 1$ B、 $x + 1$ C、 $x^{2} - 1$ D、 ${(x - 1)}^{2}$

查看试题解析
6. 下列命题中是真命题的是（）

A、实数包括正实数与负实数 B、数轴上的点与有理数一一对应 C、两边及其一边对角对应相等的两个三角形全等 D、若 $| a | = | b |$ ，则 $a^{2} = b^{2}$

查看试题解析
7. 如图，已知∠ABC＝∠BAD ，再添加一个条件，仍不能判定△ABC≌△BAD的是（　　）

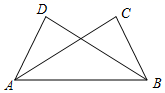A、AC＝BD B、∠C＝∠D C、AD＝BC D、∠ABD＝∠BAC

查看试题解析
8. 现在有若干张如图所示的正方形A类、B类卡片和长方形C类卡片，如果要拼成一个长为 $(3 a + b)$ 、宽为 $(2 a + 3 b)$ 的大长方形，则需要C类卡片（）

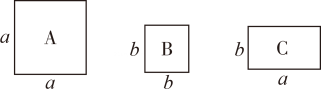A、11张 B、12张 C、13张 D、14张

查看试题解析
9. 如图通过将左图裁剪、用两块梯形拼接成右图，体现了什么数学公式（）

A、a²﹣b²＝（a+b）（a﹣b） B、（a﹣b）²＝a²﹣2ab+b² C、a（a+b）＝a²+ab D、（a+b）²＝a²+2ab+b²

查看试题解析
10. 如图，大正方形与小正方形的面积之差是40，则阴影部分的面积是（）

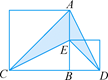A、80 B、40 C、20 D、10

查看试题解析

二、填空题

11. 等腰三角形的一个外角是110°，它的顶角的度数是．

查看试题解析
12. 有个数值转换器，原理如图所示，当输入x为27时，输出的y值是.

查看试题解析
13. 计算 ${(\frac{2}{3})}^{2015} \times {(- \frac{3}{2})}^{2016} =$ .

查看试题解析
14. 若 $(x + a) (x - 3)$ 的积中不含x的一次项，则a的值是.

查看试题解析
15. 若 $3^{x} = 20$ ， $9^{y} = 5$ ，则 $3^{x - 2 y}$ ＝.

查看试题解析
16. 如果 $4 x^{2} - (a - b) x + 9$ 是一个整式的平方，则 $2 a - 2 b$ 的值是.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{- 8} + | - \sqrt{4} | + \sqrt{{(- 3)}^{2}} - | 3 - π |$ ；

(2)、 ${(- \frac{1}{2} a^{2})}^{3} \cdot {(- 4 b^{3})}^{2} \div {(a b)}^{4}$ .

查看试题解析
18. 分解因式：

(1)、 $81 m^{3} - 54 m^{2} + 9 m$ ；

(2)、 $(a - b) m^{2} + 4 (b - a) n^{2}$ .

查看试题解析
19. 若x+y=5，xy=4..

(1)、求 $x^{2} + y^{2}$ 的值

(2)、求x-y的值．

查看试题解析
20. 先化简，再求值： $[{(2 x + y)}^{2} - （ 2 x - y ） (2 x + y)] \div (2 y)$ ，其中x=2，y=-1．

查看试题解析
21. 如图，点 $E ， F$ 在线段 $A C$ 上， $A E = C F ， D E ⊥ A C ， B F ⊥ A C$ ，垂足分别为 $E ， F ， A B = C D$ .

求证：

(1)、 $D E = B F$ ；

(2)、 $A B / / C D$

查看试题解析
22. 如图，已知△ABC与△ADE为等边三角形，D为BC延长线上的一点.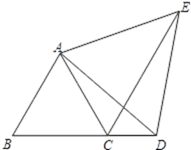

(1)、求证：△ABD≌△ACE；

(2)、求证：CE平分∠ACD.

查看试题解析
23. 阅读理解：
例：已知： $m^{2} + 2 mn + 2 n^{2} - 6 n + 9 = 0$ ，

求： $m$ 和 $n$ 的值.

解： $∵$ $m^{2} + 2 mn + 2 n^{2} - 6 n + 9 = 0$ ，

$∴$ $m^{2} + 2 mn + n^{2} + n^{2} - 6 n + 9 = 0$ ，

$∴$ ${(m + n)}^{2} + {(n - 3)}^{2} = 0$ ，

$∴$ $m + n = 0$ ， $n - 3 = 0$ ，

$∴$ $m = - 3$ ， $n = 3$ ，

解决问题：

(1)、若 $x^{2} - 4 xy + 5 y^{2} + 2 y + 1 = 0$ ，求x、y的值；

(2)、已知 $a$ ， $b$ ， $c$ 是 $△ ABC$ 的三边长且满足 $a^{2} + b^{2} = 10 a + 12 b - 61$ ，
①直接写出a=.b=.

②若 $c$ 是 $△ ABC$ 中最短边的边长（即c<a；c<b），且 $c$ 为整数，直接写出 $c$ 的值可能是.

查看试题解析
24. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．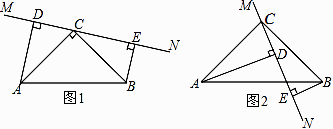

(1)、当直线MN绕点C旋转到图1的位置时，求证：DE=AD+BE；

(2)、当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，请写出新的结论并说明理由．

查看试题解析