河南省周口市太康县2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-28 类型:期中考试
一、单选题
-
1. 有下列说法:①无理数是开方开不尽的数;②每一个无理数都可以用数轴上的一个点表示出来;③ 的算术平方根是 ;④0的平方根和立方根都是 ,其中结论正确的有( )A、 个 B、 个 C、 个 D、 个2. 下列计算正确的是( )A、 B、 C、 D、3. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解4. 下列命题:
①相等的角是对顶角;
②两个全等三角形对应边上的中线相等;
③有两边和一角分别相等的两个三角形全等;
④锐角三角形的任意一个外角大于任何一个内角.
其中真命题的个数是( )
A、1个 B、2个 C、3个 D、4个5. 下列因式分解正确的是( )A、 B、 C、 D、6. 已知 ,a介于两个连续自然数之间,则下列结论正确的是( )A、 B、 C、 D、7. 如图,已知E,B,F,C四点在一条直线上, , ,添加以下条件之一,仍不能证明 ≌ 的是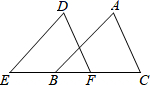 A、 B、 C、 D、8. 下列各图中a、b、c为△ABC的边长,根据图中标注数据,判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是( )
A、 B、 C、 D、8. 下列各图中a、b、c为△ABC的边长,根据图中标注数据,判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是( )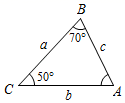 A、
A、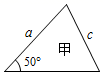 B、
B、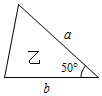 C、
C、 D、
D、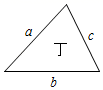 9. 如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( )
9. 如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( )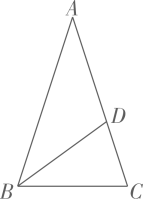 A、 B、 C、a-b D、b-a10. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论:
A、 B、 C、a-b D、b-a10. 如图,在 和 中, , , , .连接 、 交于点M,连接 .下列结论: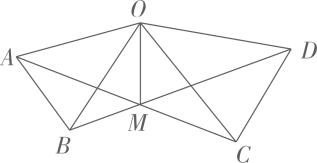
① ;② ;③ 平分 ;④ 平分
其中正确的结论个数有( )个.
A、4 B、3 C、2 D、1二、填空题
-
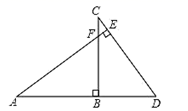
11. 已知:一个正数的两个平方根分别是 和 ,则 的值是.12. 已知 ,则代数式 的值为.13. 如图,已知 CB⊥AD,AE⊥CD,垂足分别为 B、E,AE、BC 相交于点 F,AB=BC,若 AB=8,CF=2,则 BD=.
 14. 如图, 平分 , , 的延长线交 于点E,若 ,则 的度数为.
14. 如图, 平分 , , 的延长线交 于点E,若 ,则 的度数为.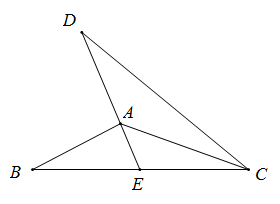 15. 如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE//BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF>CF;⑤若∠A=80°,则∠BFC=130°.其中正确的有.(填正确的序号)
15. 如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE//BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF>CF;⑤若∠A=80°,则∠BFC=130°.其中正确的有.(填正确的序号)
三、解答题
-
16. 化简;(1)、(2)、17. 把下列各式因式分解:(1)、 ;(2)、 .18. 先化简,再求值: ,其中 .19. 已知实数a+9的一个平方根是﹣5,2b﹣a的立方根是﹣2,求 +2 的算术平方根.20. 如图,点C , E , F , B在同一直线上,点A , D在BC异侧,AB∥CD , AE=DF , ∠A=∠D .
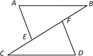 (1)、求证:AB=CD;(2)、若AB=CF , ∠B=40°,求∠D的度数.21.(1)、如图(1),已知CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌△BCE.
(1)、求证:AB=CD;(2)、若AB=CF , ∠B=40°,求∠D的度数.21.(1)、如图(1),已知CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌△BCE.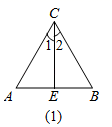 (2)、如图(2),已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.
(2)、如图(2),已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由. 22. (阅读材料)
22. (阅读材料)我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为x的正方形,乙种纸片是边长为y的正方形,丙种纸片是长为y,宽为x的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
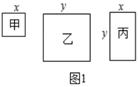
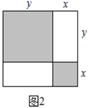 (1)、(理解应用)
(1)、(理解应用)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(2)、(拓展升华)利用(1)中的等式解决下列问题.
①已知 , ,求 的值;
②已知 ,求 的值.
23. 如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.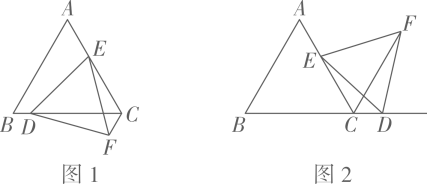 (1)、(问题解决)
(1)、(问题解决)如图1,若点D在边BC上,求证:CE+CF=CD;
(2)、(类比探究)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.