河南省郑州市中牟县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{7}$ 的相反数是（）

A、 $\pm \sqrt{7}$ B、 $- \sqrt{7}$ C、 $\frac{\sqrt{7}}{7}$ D、 $- \frac{\sqrt{7}}{7}$

查看试题解析
2. 下列各组数分别为一个三角形的三边长，其中能构成直角三角形的一组是（）

A、5，11，12 B、2，2，3 C、3，4，5 D、4，5，6

查看试题解析
3. 下列说法中不正确的是（）

A、10的平方根是 $\pm \sqrt{10}$ B、-8是64的一个平方根 C、27的立方根是3 D、 $\frac{4}{9}$ 的平方根是 $\frac{2}{3}$

查看试题解析
4. 下列各点在一次函数y=2x﹣3的图象上的是（）

A、（2，3） B、（2，1） C、（0，3） D、（3，0

查看试题解析
5. 下列各数中，与 $\sqrt{6} - 3$ 的乘积是有理数的是（）

A、 $\sqrt{6} + 3$ B、 $\sqrt{6} - 3$ C、 $3 - \sqrt{6}$ D、 $\sqrt{6} + \sqrt{3}$

查看试题解析
6. 如图，数轴上有O，A，B，C，D五个点，根据图中各点所表示的数，判断 $\sqrt{15}$ 在数轴上的位置会在下列哪一条线段上（）

A、 $O A$ B、 $A B$ C、 $B C$ D、 $C D$

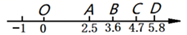查看试题解析
7. 将平面直角坐标系内的△ABC的三个顶点坐标的横坐标乘以﹣1，纵坐标不变，则所得的三角形与原三角形（）

A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、无任何对称关系

查看试题解析
8. 如图，李强和同事驾驶快艇执行巡逻任务，他们从岛屿 $A$ 处向正南方向航行到 $B$ 处时，向右转 $60 °$ 航行到 $C$ 处，再向左转 $80 °$ 继续航行，此时快艇的航行方向为（）

A、南偏东 $20 °$ B、南偏东 $80 °$ C、南偏西 $20 °$ D、南偏西 $80 °$

查看试题解析
9. 1876年，美国总统伽菲尔德利用如图所示的方法验证了勾股定理，其中两个全等的直角三角形的边 $A E$ ， $E B$ 在一条直线上，证明中用到的面积相等关系是（）

A、 $S_{△ E D A} = S_{△ C E B}$ B、 $S_{△ E D A} + S_{△ C D E} + S_{△ C E B} = S_{四边形 A B C D}$ C、 $S_{△ E D A} + S_{△ C E B} = S_{△ C D E}$ D、 $S_{四边形 A E C D} = S_{四边形 D E B C}$

查看试题解析
10. 育红中学八五班的数学社团在做如下的探究活动：在平面直角坐标系中，一个智能机器人接到如下指令：从原点 $O$ 出发，按向上、向右、向下、向右的方向依次移动，每次移动1个单位长度，其移动路线如图所示，第1次移动到点 $A_{1}$ ，第2次移动到点 $A_{2}$ ……第n次移动到点 $A_{n}$ ，则 $△ O A_{2} A_{2021}$ 的面积是（）

A、1009 B、 $\frac{1011}{2}$ C、505 D、 $\frac{1009}{2}$

查看试题解析

二、填空题

11. -64的立方根是。

查看试题解析
12. 如图，在象棋棋盘上，“馬”位于点 $(2 ， 2)$ ，“炮”位于点 $(- 1 ， 2)$ ，写出“兵”所在的位置：.

查看试题解析
13. 写出两个m的值，使相应的一次函数 $y = m x + 4$ 的值都是随x的增大而减小，那么 $m =$ .

查看试题解析
14. 如图所示是一个长方体纸盒，纸盒的长为 $12 cm$ ，宽为 $9 cm$ ，高为 $5 cm$ ，一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G，蚂蚁爬行的最短路程是 $cm$ .

查看试题解析
15. 某个周末，李海和他的叔叔先后从家出发，他们沿着同一条公路匀速前往某景区，李海8点骑着电动车出发，如图是他行驶路程 $s (km)$ 随行驶时间 $t (h)$ 变化的图象.李海的叔叔开车9点出发，若要在10点至11点之间（含10点和11点）追上李海，则叔叔的开车速度 $v (km/h)$ 的范围是.

查看试题解析

三、解答题

16. 计算：

(1)、 $2 \sqrt{3} - \sqrt{8} + \frac{1}{2} \sqrt{12} + \frac{1}{5} \sqrt{50}$ ；

(2)、 ${(\sqrt{2} + 1)}^{2} - \frac{\sqrt{12} - \sqrt{6}}{\sqrt{3}}$ .

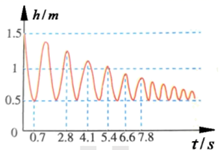
查看试题解析
17. 周末了，小红带弟弟一起荡秋千，秋千离地面的高度 $h (m)$ 与摆动时间 $t (s)$ 之间的关系如图所示.

(1)、根据函数的定义，请判断变量h是否为t的函数？

(2)、当 $t = 2.8 s$ 时，h的值是多少？并说明它的实际意义；

(3)、秋千摆动第二个来回需要多少时间？

查看试题解析
18. 育新实验学校八（二）班的学生从学校O点出发，要到某基地进行为期一周的校外实践活动，他们第一天的任务是进行体能训练，学生们先向正西方向行走了 $2 km$ 到A处，又往正南方向行走 $3 km$ 到B处，然后又折向正东方向行走 $6 km$ 到C处，再向正北方向走 $5 km$ 才到校外实践基地P处.如图，以点O为原点，取O点的正东方向为x轴的正方向，取O点的正北方向为y轴的正方向，以 $500 m$ 为一个单位长度建立平面直角坐标系.

(1)、在平面直角坐标系中，画出学生体能训练的行走路线图；

(2)、分别写出A，B，C，P点的坐标；

(3)、请在横线上直接写出O，P两点之间的距离.

查看试题解析
19. 我们在学习第二章《实数》这节课时，画了如图所示的图形，即“以数轴上单位长度为1的线段为边作一个正方形，然后以原点O为圆心， $O B$ 的长为半径作弧，交数轴的正半轴于点A”，请解答下列问题：

(1)、线段 $O A$ 的长度是多少？

(2)、这个图形的目的是为了说明什么？

(3)、请在数轴上画出表示 $- \sqrt{10}$ 的点P.（不写作法，保留作图痕迹）

查看试题解析
20. 如图，一牧童的家在点A处，他和哥哥一起在点C处放马，点A，C到河岸的距离分别是 $A B = 500 m$ ， $C D = 700 m$ ，且B，D两地间的距离为 $600 m$ .夕阳西下，弟兄俩准备从C点将马牵到河边去饮水，再赶回家，为了使所走的路程最短.

(1)、他们应该将马赶到河边的什么地点？请在图中画出来；

(2)、请求出他们至少要走的路程.

查看试题解析
21. 已知一次函数 $y = k x + 3$ 与x轴交于点 $A (2 ， 0)$ ，与y轴交于点B.

(1)、求一次函数的表达式及点B的坐标；

(2)、画出函数 $y = k x + 3$ 的图象；

(3)、过点B作直线 $B P$ 与x轴交于点P，且 $O P = 2 O A$ ，求 $△ A B P$ 的面积.

查看试题解析
22. 已知点 $A (3 a + 2 ， 2 a - 4)$ ，试分别根据下列条件，求出a的值并写出点A的坐标.

(1)、点A在x轴上；

(2)、点A与点 $A' (- 4 ， - \frac{8}{3})$ 关于y轴对称；

(3)、经过点 $A (3 a + 2 ， 2 a - 4)$ ， $B (3 ， 4)$ 的直线，与x轴平行；

(4)、点A到两坐标轴的距离相等.

查看试题解析
23. 上个周末，姚家中学的李老师开车带着家人从学校出发，沿着图①中的线路去绿博园、中牟黄河滩区游玩、然后去官渡中学探望朋友.李老师一家早上7：30开着电动汽车从学校出发行走一段时间到绿博园，在绿博园游玩了一段时间；又开车去雁鸣湖镇辖区的黄河滩，他们在滩区游玩了 $1.5 h$ ；然后在中午12：30赶到官渡中学（电动汽车的行驶速度是 $40 km/h$ ）.图②中的图象表示李老师一家所行驶的路程 $y (km)$ 与时间 $x (h)$ 的函数关系.

请结合图中信息解答下列问题：

(1)、点A的坐标是，他们在绿博园游玩了h，线段 $O A$ 的函数表达式是；

(2)、线段 $O A$ ， $B C$ ， $D E$ 平行吗？请简单说明理由.

(3)、请求出线段 $B C$ 的函数表达式；

(4)、如果李辉在11：30骑电动车从官渡中学出发，以 $20 km/h$ 的速度沿图①中的线路前往黄河滩区游玩，那么李辉在几点钟会和李老师相遇？

查看试题解析