河南省新乡市延津县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-28 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列各组线段不能组成三角形的是（ ）
    A、4cm、4cm、5cm B、4cm、6cm、11cm C、4cm、5cm、6cm D、5cm、12cm、13cm

    查看试题解析

  • 2. 三角形一个外角小于与它相邻的内角，这个三角形（   ）
    A、是钝角三角形 B、是锐角三角形 C、是直角三角形 D、属于哪一类不能确定.

    查看试题解析

  • 3. 若一个正多边形的每个内角度数都为135°，则这个正多边形的边数是（   ）
    A、6 B、8 C、10 D、12

    查看试题解析

  • 4. 如图，在△AEC中，点D和点F分别是AC和AE上的两点，连接DF，交CE的延长线于点B，若∠A＝25°，∠B＝45°，∠C＝36°，则∠DFE＝（　　）

    A、103° B、104° C、105° D、106°

    查看试题解析

  • 5. 如图，已知AC平分∠PAQ，点B、B′分别在边AP、AQ上，如果添加一个条件，即可推出AB=A B′，那么该条件不可以是（   ）

    A、BB′⊥AC B、CB=CB′ C、∠ACB=∠ACB′ D、∠ABC=∠AB′C

    查看试题解析

  • 6. 如图所示，有一个简易平分角的仪器（四边形ABCD），其中AB＝AD ， BC＝DC ， 将点A放在角的顶点处，AB和AD沿着角的两边张开，并分别与AQ ， AP重合，沿对角线AC画射线AE ， AE就是∠PAQ的平分线这个平分角的仪器的制作原理是（   ）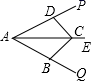

    A、角平分线性质 B、AAS C、SSS D、SAS

    查看试题解析

  • 7. 如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S△OAB：S△OBC：S△OAC=（   ）

    A、1：1：1 B、1：2：3 C、2：3：4 D、3：4：5

    查看试题解析

  • 8. 如图，在 △ABC 中， ∠BAC=90∘ ， AB=3 ， AC=4 ， BC=5 ， EF 垂直平分 BC ，点 P 为直线 EF 上的任一点，则 AP+BP 的最小值是（　　）

    A、3 B、4 C、5 D、6

    查看试题解析

  • 9.

    如下图，△MNP中，∠P=60°，MN=NP，MQ⊥PN，垂足为Q，延长MN至G，取NG=NQ，若△MNP的周长为12，MQ=a，则△MGQ周长是（　　）

    A、8+2a B、8+a C、6+a D、6+2a

    查看试题解析

  • 10. 如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点．若 AE=2 ，当 EF+CF 取得最小值时，则 ∠ECF 的度数为（    ）

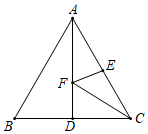    A、15° B、225° C、30° D、45°

    查看试题解析

二、填空题

  • 11. 如图，若 Δ ABC≌ Δ DEF，BE=18，BF=5，则 FC 的长度是.

    查看试题解析

  • 12. 如图，六边形ABCDEF中，AB∥DC，∠1、∠2、∠3、∠4分别是∠BAF、∠AFE、∠FED、∠EDC的外角，则∠1+∠2+∠3+∠4＝.

    查看试题解析

  • 13. 若点A（m+2，3）与点B（﹣4，n+5）关于x轴对称，则m+n＝.

    查看试题解析

  • 14. 如图△ABO的边OB在x轴上，∠A=2∠ABO，OC平分∠AOB，若AC=2，OA=3，则点B的坐标为　

    查看试题解析

  • 15. 如图，△ABC纸片中，AB=AC，∠BAC＝90°，BC＝8，沿过点C的直线折叠这个三角形，使点A落在BC边上的点F处，折痕为CD，BE⊥CD，垂足E在CD的延长线上，则结论①DF=DA；②∠ABE＝22.5 ° ；③△BDF 的周长为8；④CD=2BE.正确的是（填上正确的结论序号）.

    查看试题解析

三、解答题

  • 16. 已知：如图，在△ABC中，点D是BC上一点，∠1＝80°，AB＝AD＝DC.求：∠C的度数.

    查看试题解析

  • 17.   
    (1)、某多边形的内角和与外角和的总和为2 160°，求此多边形的边数；
    (2)、某多边形的每一个内角都等于150°，求这个多边形的内角和.

    查看试题解析

  • 18. 如图，线段AB和BC，交于B点：

    (1)、请你用尺规作图的方法作出线段AB和BC的垂直平分线.（不写作法，保留作图痕迹）
    (2)、如果线段AB和BC的垂直平分线交于点P，若AB＝BC，求证：PB平分∠ABC.

    查看试题解析

  • 19. 一个等腰三角形的周长为28cm.
    (1)、如果底边长是腰长的1.5倍，求这个等腰三角形的三边长；
    (2)、如果一边长为10cm，求这个等腰三角形的另两边长.

    查看试题解析

  • 20. 如图，Rt△ABC的直角顶点C置于直线l上，AC＝BC，现过A．B两点分别作直线l的垂线，垂足分别为点D．E．

    (1)、求证：△ACD≌△CBE．
    (2)、若BE＝3，DE＝5，求AD的长．

    查看试题解析

  • 21. （ 1 ）如图，请在方格纸中画出△ABC关于x轴的对称图形△A′B′C′.

    （ 2 ）写出对称点的坐标：A′（ 　， 　），B′（　  　，　 　），C′（  　，　 　）.

    （ 3 ）△ABC的面积是           .

    （ 4 ）请在图中找出一个格点D，画出△ACD，使△ACD与△ABC全等.

    查看试题解析

  • 22. 如图，在△ABC中，∠ABC＝90°，AD∥BC，AB＝BC，E是AB的中点，CE⊥BD.

    (1)、求证：△ABD≌△BCE.
    (2)、求证：AC是线段ED的垂直平分线.

    查看试题解析

  • 23. 已知四边形ABCD中，AB⊥AD，BC⊥CD，AB＝BC，∠ABC＝120°，∠MBN＝60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F.

    (1)、当∠MBN绕B点旋转到AE＝CF时（如图1），求证：△ABE≌△CBF.
    (2)、当∠MBN绕点B旋转到AE≠CF时，如图2，猜想线段AE，CF，EF有怎样的数量关系，并证明你的猜想.
    (3)、当∠MBN绕点B旋转到图3这种情况下，猜想线段AE，CF，EF有怎样的数量关系，并证明你的猜想.

    查看试题解析