河南省商丘市柘城县2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-09-28 类型：期中考试
一、单选题
-
1. 下列垃圾分类的图标（不含文字与字母部分）中，是轴对称图形的是（ ）A、
B、
C、
D、
2.如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）
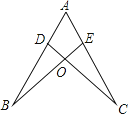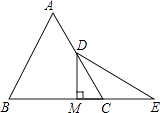
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD3. 已知点A（a，2019）与点B（2020，b）关于x轴对称，则a+b的值为（ ）A、﹣1 B、1 C、2 D、34. 如图，在△ABC中，AB＝AC，且D为BC上一点，CD＝AD，AB＝BD，则∠B的度数为（ ）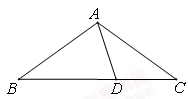
A、30° B、36° C、40° D、45°5. 下列长度的三条线段不能组成三角形的是（ ）A、3，4，5 B、1， ，2 C、6，8，10 D、1.5，2.5，46. 如图，在△ABC中，CD是∠ACB的外角平分线，且CD∥AB，若∠ACB＝100°，则∠B的度数为（ ）
A、35° B、40o C、45o D、50o7. 一个等腰三角形的两边长分别是3cm和7cm，则它的周长为（ ）A、17cm B、15cm C、13cm D、13cm或17cm8. 如图，∠A=80°，点O是AB，AC垂直平分线的交点，则∠BCO的度数是（ ）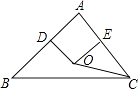
A、40° B、30° C、20° D、10°9. 如图，在 中， ， 是 的角平分线交 于点D， 于E点，下列四个结论中正确的有（ ）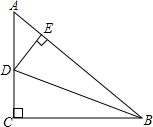
① ② ③ ④
A、 个 B、 个 C、 个 D、 个10. 如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是（ ）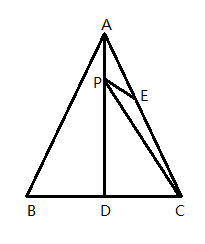
A、30° B、45° C、60° D、90°二、填空题
-
11. 一个正多边形的一个外角为30°，则它的内角和为 ．12. 若△ABC≌△DEF，AB＝2，AC＝4，且△DEF的周长为奇数，则EF的值为.13. 等腰 周长为 ，其中两边长的差为 ，则腰长为 .14. 如图， ， ，请你添加一个适当的条件： ， 使得
15. 如图，将Rt△ABC沿BC方向平移得Rt△DEF，其中AB＝8，BE＝8，DM＝5，则阴影部分的面积是.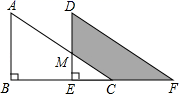
三、解答题
-
16. 如图，在Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，连接CD，交BE于点F.
求证：BE垂直平分CD.
17. 如图，在△ABC中，AB＝AC，点D、E分别是AB、AC的中点，点F是BE、CD的交点.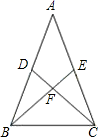
(1)、请写出图中所有的全等三角形；(2)、任选（1）中的一对全等三角形加以证明.18. 如图，△ABC的三个顶点坐标分别是A（3，3），B（1，1），C（4，﹣1）.
（ 1 ）直接写出点A，B，C关于x轴对称的点A1 ， B1 ， C1 ， 的坐标：A1（ ， ），B1（ ， ），C1（ ， ）；
（ 2 ）在图中作出△ABC关于y轴对称的图形△A2B2C2；
（ 3 ）在图中作出△A2B2C2关于x轴对称图形△A3B3C3.
19. 如图，在△AEC和△DFB中，∠E＝∠F，点A，B，C，D在同一直线上，有如下三个关系式：①AE∥DF，②AB＝CD，③CE＝BF.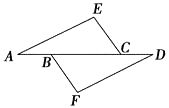
(1)、请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题(用序号写出命题书写形式：“如果⊗，⊗，那么⊗”)；
(2)、选择(1)中你写出的一个命题，说明它正确的理由．20. 如图，在△ABC中，AB=AC，D是BC边上的中点，连接AD，BE平分∠ABC交AC于点E，过E作EF∥BC交AB于点F.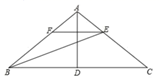
(1)、若∠C=36°，求∠BAD的度数；(2)、求证：FB=FE.
