河南省平顶山市叶县2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-28 类型:期中考试
一、单选题
-
1. 在 , ,0, , , , (相邻两个5之间依次多一个1)中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 下列四个图象中,y不是x的函数图象的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列说法:①±3都是27的立方根;② 的算术平方根是± ;③﹣ =2;④ 的平方根是±4;⑤﹣9是81的算术平方根,其中正确的有( )A、1个 B、2个 C、3个 D、4个4. 已知一次函数 ,y随着x的增大而增大,且 ,则在直角坐标系内它的大致图象是( )A、
3. 下列说法:①±3都是27的立方根;② 的算术平方根是± ;③﹣ =2;④ 的平方根是±4;⑤﹣9是81的算术平方根,其中正确的有( )A、1个 B、2个 C、3个 D、4个4. 已知一次函数 ,y随着x的增大而增大,且 ,则在直角坐标系内它的大致图象是( )A、 B、
B、 C、
C、 D、
D、 5. 估计a 1的值应在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间6. 如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )
5. 估计a 1的值应在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间6. 如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )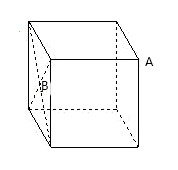 A、9 B、 C、 D、127. 给出下列命题:
A、9 B、 C、 D、127. 给出下列命题:①如果a、b、c为一组勾股数,那么 、 、 仍是一组勾股数;
②如果直角三角形的三边两边长为3和4,那么另一边长的平方必是25;
③如果一个三角形的三边长是12,25,21,那么三角形必直角三角形;
④一个等腰直角三角形的三边长分别为a、b、c,其中a是斜边长,那么 .
其中正确的是( )
A、①② B、①③ C、②④ D、①④8. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )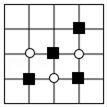 A、(﹣2,1) B、(﹣1,1) C、(1,﹣2) D、(﹣1,﹣2)9. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A、(﹣2,1) B、(﹣1,1) C、(1,﹣2) D、(﹣1,﹣2)9. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )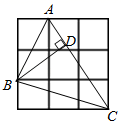 A、 B、 C、 D、10. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图象得出如下结论:
A、 B、 C、 D、10. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图象得出如下结论:①快车途中停留了 ; ②快车速度比慢车速度多 ;
③图中 ; ④快车先到达目的地.
其中正确的是( )
 A、①③ B、②③ C、②④ D、①④
A、①③ B、②③ C、②④ D、①④二、填空题
-
11. 写出一个比2大比3小的无理数(用含根号的式子表示) .
12. 函数 是一次函数,则 .13. 如图所示,每个小正方形的边长为1,A、B、C是小正方形的顶点,则 的度数为. 14. 平面直角坐标系中,点 , , ,若 轴,当线段 取最小值时,点C的坐标为.15. 如图,在长方形 中, , ,E是 边上一点,将长方形沿 折叠,点B落在点 处,当 是直角三角形时, 的长为.
14. 平面直角坐标系中,点 , , ,若 轴,当线段 取最小值时,点C的坐标为.15. 如图,在长方形 中, , ,E是 边上一点,将长方形沿 折叠,点B落在点 处,当 是直角三角形时, 的长为.
三、解答题
-
16. 计算(1)、 ;(2)、 ;(3)、 ;(4)、 .17. 已知 的立方根是3, 的算术平方根是4,c是 的整数部分.(1)、求a,b,c的值;(2)、求 的平方根.18. 如图所示,在平面直角坐标系中,△ABC各顶点的坐标分别为A(4,0),B(-1,4),C(-3,1).
 (1)、作出△A′B′C′,使△A′B′C′和△ABC关于x轴对称;(2)、写出点A′, B′,C′的坐标;(3)、求△ABC的面积.19.(1)、已知点 的横坐标减纵坐标的差为6,求这个点到x轴、y轴的距离;(2)、已知点 到两坐标轴的距离相等,且在第二象限,求点A的坐标;(3)、已知线段 平行于y轴,点A的坐标为 ,且 ,求点B的坐标.20. 如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.
(1)、作出△A′B′C′,使△A′B′C′和△ABC关于x轴对称;(2)、写出点A′, B′,C′的坐标;(3)、求△ABC的面积.19.(1)、已知点 的横坐标减纵坐标的差为6,求这个点到x轴、y轴的距离;(2)、已知点 到两坐标轴的距离相等,且在第二象限,求点A的坐标;(3)、已知线段 平行于y轴,点A的坐标为 ,且 ,求点B的坐标.20. 如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.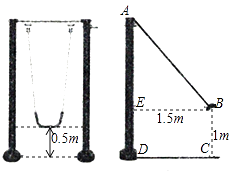
21. 在 中, , .过点A在 外作直线 , 于M, 于N. (1)、证明: ;(2)、若 , , .试利用此图验证勾股定理 .22. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
(1)、证明: ;(2)、若 , , .试利用此图验证勾股定理 .22. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身x(次),按照方案一所需费用为 ,(元),且 ;按照方案二所需费用为 (元) ,且 其函数图象如图所示.
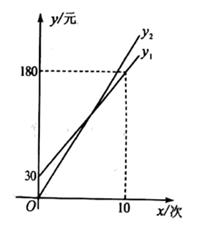 (1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.23. 如图,直线y=kx﹣2与x轴,y轴分别交于B,C两点,其中OB=1.
(1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.23. 如图,直线y=kx﹣2与x轴,y轴分别交于B,C两点,其中OB=1. (1)、求k的值;(2)、若点A(x,y)是第一象限内的直线y=kx﹣2上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、在(2)的条件下,探索:
(1)、求k的值;(2)、若点A(x,y)是第一象限内的直线y=kx﹣2上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、在(2)的条件下,探索:①当点A运动到什么位置时,△AOB的面积是1;
②在①成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形?若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.