河南省平顶山市舞钢市2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. 以下列长度的线段为边，能构成直角三角形的是（　　）

A、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ B、1，2， $\sqrt{5}$ C、6，8，12 D、5，11，13

查看试题解析
2. 在实数 $\sqrt{5}, \frac{22}{7}, 0, \frac{π}{2} ， \sqrt{36}, - 1.414$ ，有理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，在数轴上表示 $\sqrt{7}$ 的点在哪两个字母之间（）

A、B 与 C B、A 与 B C、A 与 C D、C 与 D

查看试题解析
4. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{10}$ D、 $\sqrt{16}$

查看试题解析
5. 已知M（a，3）和N（4，b）关于x轴对称，则（a+b）²⁰²⁰的值为（　）

A、1 B、﹣1 C、7²⁰²⁰ D、﹣7²⁰²⁰

查看试题解析
6. 如图，正方形ABCD的边长为4，点A的坐标为(－1，1)，AB平行于x轴，则点C的坐标为（）

A、(3，1) B、(－1，1) C、(3，5) D、(－1，5)

查看试题解析
7. 已知一个正数的两个平方根分别为 $3 a - 5$ 和 $7 - a$ ，则这个正数的立方根是（）

A、4 B、3 C、2 D、1

查看试题解析
8. 已知正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝﹣kx+k的图象大致是（　　）

A、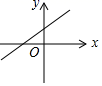 B、 C、 D、

查看试题解析
9. 如图，一只蚂蚁从长为2cm、宽为2cm，高是3 $c m$ 的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是（） $c m$ .

A、3 B、2 C、5 D、7

查看试题解析
10. 八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线 $l$ 将这八个正方形分成面积相等的两部分，则该直线 $l$ 的解析式为（）

A、 $y = \frac{3}{5} x$ B、 $y = \frac{9}{10} x$ C、 $y = \frac{3}{4} x$ D、 $y = x$

查看试题解析

二、填空题

11. 在△ABC中，∠C＝90°，BC＝2，AC＝2 $\sqrt{2}$ ，则AB＝.

查看试题解析
12. 若 $a$ ， $b$ 分别为 $\sqrt{11}$ 的整数部分和小数部分，则a-b的值为.

查看试题解析
13. 已知 $A (2 a + 1 ， 3)$ ， $B (- 5 ， 3 b - 3)$ 关于原点对称，则a+b= ．

查看试题解析
14. 如图，在平面直角坐标系中，点A、B的坐标分别为（1，4）、（4，4），若直线y＝2x+b与线段AB有公共点，则b的值可以为.（写出一个即可）

查看试题解析
15. 在平面直角坐标系中，一个智能机器人接到的指令是：从原点O出发，按“向上 $\to$ 向右 $\to$ 向下 $\to$ 向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点 $A_{1} ，$ 第二次移动到点 $A_{2}$ ….第 $n$ 次移动到点 $A_{n} ，$ 则点 $A_{2020}$ 的坐标是.

查看试题解析

三、解答题

16. 计算

(1)、 $\frac{\sqrt{12} + \sqrt{27}}{\sqrt{3}} - {(\sqrt{3} - \sqrt{2})}^{2} - | - \sqrt{6} |$ ；

(2)、 $\sqrt{{(- 5)}^{2}} + | \sqrt{3} - \frac{5}{2} | - {(\sqrt{2})}^{2} - \sqrt[3]{- \frac{125}{8}}$ .

查看试题解析
17. 在解决问题“已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值”时，小明是这样分析与解答的：
∵ $a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，

∴ $a - 2 = - \sqrt{3}$

∴ ${(a - 2)}^{2} = 3$ ，即 $a^{2} - 4 a + 4 = 3$

∴ $a^{2} - 4 a = - 1$

∴ $2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ .

请你根据小明的分析过程，解决如下问题：

(1)、化简： $\frac{2}{\sqrt{5} - \sqrt{3}}$ ；

(2)、若 $a = \frac{1}{\sqrt{2} - 1}$ ，求 $3 a^{2} - 6 a - 1$ 的值.

查看试题解析
18. 七年级（2）班的同学组织到人民公园游玩，张明、王励、李华三位同学和其他同学走散了，同学们已到中心广场，他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置，张明说他的坐标是 $(200 ， - 200)$ ，王励说他的坐标是 $(- 200 ， - 100)$ ，李华说他的坐标是 $(- 300 ， 200)$ .

（ 1 ）请你根据题目条件，在图中画出平面直角坐标系；

（ 2 ）写出这三位同学所在的位置；

（ 3 ）写出除了这三位同学所在位置外，图中其余两个景点的坐标.

查看试题解析
19. 已知直线l与直线 $y = 2 x - 2$ 平行，且经过点 $(2 ， 6)$ .

(1)、求直线l的关系式；

(2)、直接在坐标系中画出直线l的图象.

查看试题解析
20. 国庆期间某一位公司老板准备和员工去上海旅游，甲旅行社承诺：“老板一人免费，员工可享受八折优惠”；乙旅行社承诺：“包括老板在内所有人按全票的七五折优惠”，若全票价为2000元.

(1)、设参加旅游的员工人数为x，甲、乙旅行社收费分别为y_甲（元）和y_乙（元），分别写出两个旅行社收费的表达式；

(2)、当员工有10人时，哪家旅行社更优惠？

(3)、员工人数为多少时，两家旅行社花费一样？据此，请根据旅游员工人数的多少，为公司老板选择哪家旅行社提出合理化建议（只说出结果）.

查看试题解析
21. 课堂上学习了勾股定理后，知道“勾三、股四、弦五”．王老师给出一组数让学生观察：3、4、5；5、12、13；7、24、25；9、40、41；…，学生发现这些勾股数的勾都是奇数，且从 3 起就没有间断过，于是王老师提出以下问题让学生解决．

(1)、请你根据上述的规律写出下一组勾股数：11、、；

(2)、若第一个数用字母a(a为奇数，且a≥3)表示，那么后两个数用含a的代数式分别怎么表示？小明发现每组第二个数有这样的规律 $4 = \frac{3^{2} - 1}{2}$ ， $12 = \frac{5^{2} - 1}{2}$ ， $24 = \frac{7^{2} - 1}{2}$ ……，于是他很快表示了第二数为 $\frac{a^{2} - 1}{2}$ ，则用含a的代数式表示第三个数为；

(3)、用所学知识证明你的结论．

查看试题解析
22. 如图1，在平面直角坐标系中，一次函数y＝﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B.

(1)、线段AB，BC，AC的长分别为AB＝， BC＝， AC＝；

(2)、折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2.
①求线段AD的长；

②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由.

查看试题解析
23.

(1)、观察猜想
如图①，点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE=90°，AD=AE，则BC、BD、CE之间的数量关系为

(2)、问题解决
如图②，在Rt△ABC中，∠ABC=90°，CB=8，AB=4，以AC为直角边向外作等腰Rt△DAC连接BD，求BD的长.

(3)、拓展延伸
如图③，在四边形ABCD中，∠ABC=∠ADC=90°，CB=8.AB=4，DC=DA，则BD=

查看试题解析