江苏省扬州市江都区邵樊片2021年数学中考二模试卷

试卷更新日期：2021-09-28 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣5的相反数是（）

A、5 B、±5 C、﹣5 D、 $\sqrt{5}$

查看试题解析
2. 如图，下列几何体中，俯视图是矩形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{8} - \sqrt{3} = \sqrt{8 - 3}$ B、 $\sqrt{4} + \sqrt{9} = \sqrt{4 + 9}$ C、 $\sqrt{9} \times \sqrt{16} = \sqrt{9 \times 16}$ D、 $\sqrt{75} - \sqrt{3} = 6 \sqrt{2}$

查看试题解析
4. 徐州地铁3号线预计在今年6月底开始试运营，路线全长18.13km，全站共设站16座，一期投资13520000000元，将13520000000用科学记数法表示（）

A、1.352×10⁷ B、1352×10⁷ C、13.52×10⁹ D、1.352×10¹⁰

查看试题解析
5. 某中学八（1）班8个同学在课间进行一分钟跳绳比赛，成绩（单位：个）如下：115，138，126，143，134，126，157，118．这组数据的众数和中位数分别是（）

A、126，126 B、126，130 C、130，134 D、118，134

查看试题解析
6. 已知平行四边形 $A B C D$ 的对角线相交于点 $O$ ，补充下列四个条件，能使平行四边形 $A B C D$ 成为菱形的是（）

A、 $A B = B D$ B、 $A C = B D$ C、 $∠ D A B = 90^{\circ}$ D、 $∠ A O B = 90^{\circ}$

查看试题解析
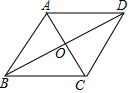7. 下列说法错误的是（）

A、定义反映出事物的本质属性．既可以做性质，也可以做判定 B、证明两个等边三角形全等，具需证明一边相等即可 C、有一个角是 $45^{\circ}$ 的等腰三角形是等腰直角三角形 D、在放大镜下，一个字可以变大，一条线段可以变长，但是一个角的大小是不变的

查看试题解析
8. 如图，在平行四边形ABCD中，∠C=120°，AD=2AB=4，点H、G分别是边CD、BC上的动点.连接AH、HG，点E为AH的中点，点F为GH的中点，连接EF，则EF的最大值与最小值的差为（）

A、1 B、 $\sqrt{3} - 1$ C、 $\frac{\sqrt{3}}{2}$ D、 $2 - \sqrt{3}$

查看试题解析

二、填空题

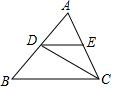
9. 实数8的立方根是．

查看试题解析
10. 函数 $y = \sqrt{x - 1}$ 中自变量x的取值范围是.

查看试题解析
11. 一个多边形的内角和是1080°则这个多边形的边数是．

查看试题解析
12. 若ab＝2，a+b＝﹣1，则代数式a²b+ab²的值等于.

查看试题解析
13. 一个圆锥的侧面展开图是半径为16cm，圆心角为120°的扇形，那么这个圆锥的底面半径为.

查看试题解析
14. 如图，已知DC为∠ACB的平分线，DE∥BC.若AD＝8，BD＝10，BC＝15，求EC的长＝.

查看试题解析
15. 如果点P（x，y）的坐标满足x+y=xy，那么称点P为“和谐点”，若某个“和谐点“P到x轴的距离为2，则P点的坐标为.

查看试题解析
16. 如图所示的网格是正方形网格，则 $∠ B A C + ∠ C D E =$ （点A，B，C，D，E是网格线交点）.

查看试题解析
17. 如图，平行四边形ABCO的边AB的中点F在y轴上，对角线AC与y轴交于点E，若反比例函数 $y = \frac{k}{x}$ （x＞0）的图象恰好经过AF的中点D，且△AEO的面积为6，则k的值为.

查看试题解析
18. 已知关于x的二次函数y=ax²+(a²-1)x-a的图象与轴的一个交点的坐标为(m，0)，若2<m<3，则a的取值范围是.

查看试题解析

三、解答题

19. 计算：

(1)、|﹣2|﹣ $\sqrt{16}$ +（﹣1）²⁰²¹；

(2)、（ $\frac{a^{2} + 1}{a}$ ﹣2）÷ $\frac{a^{2} - 1}{a}$ .

查看试题解析
20.

(1)、解方程：x²﹣4x+2＝0；

(2)、解不等式组： ${\begin{matrix} 2 x + 6 \leq 0 \\ 3 - 6 x > 0 \end{matrix}$ .

查看试题解析
21. 随着科技的进步和网络资源的丰富，在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论.为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查（每人只选一类），并根据调查结果绘制成如下两幅不完整的统计图.

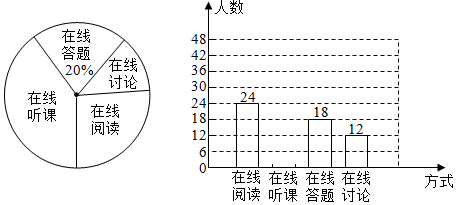
根据图中信息，解答下列问题：

(1)、求本次调查的学生总人数，并补全条形统计图；

(2)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

(3)、该校共有学生2700人，请你估计该校对在线阅读最感兴趣的学生人数.

查看试题解析
22. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标，共享出行、共享服务、共享物品、共享知识，制成编号为A、B、C、D的四张卡片（除字母和内容外，其余完全相同）.现将这四张卡片背面朝上，洗匀放好.

(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是；

(2)、小沈从中随机抽取一张卡片（不放回），再从余下的卡片中随机抽取一张，请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.（这四张卡片分别用它们的编号A、B、C、D表示）

查看试题解析
23. 在防疫新冠状病毒期间，市民对医用口罩的需求越来越大．某药店第一次用3000元购进医用口罩若干个，第二次又用3000元购进该款口罩，但第二次每个口罩的进价是第一次进价的1.25倍，购进的数量比第一次少200个．求第一次和第二次分别购进的医用口罩数量为多少个？

查看试题解析
24. 智能手机如果安装了一款测量软件“Smart Measure”后，就可以测量物高、宽度和面积等，如图，打开软件后将手机摄像头对准脚部按键，再对准头部按键，即可测量出人体的高度.测量者AB用其数学原理如图②所示，测量一棵大树CD，手机显示 $A C = 20 m$ ， $A D = 25 m$ ， $∠ C A D = 53 °$ ，求此时CD的高.（结果保留根号）（ $\sin 53 ° \approx \frac{4}{5}$ ， $\cos 53 ° \approx \frac{3}{5}$ ， $\tan 53 ° \approx \frac{4}{3}$ ）

查看试题解析
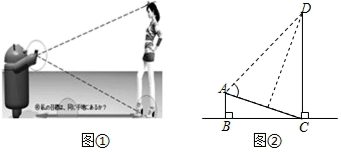25. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P.点C在OP上，且BC＝PC.

(1)、试判断直线BC与⊙O的位置关系，并说明理由；

(2)、若OA＝3，AB＝2，求BP的长.

查看试题解析
26. 如图，等边 $△ A B C$ 中，点P是 $B C$ 边上一点，作点C关于直线 $A P$ 的对称点D ，连接 $C D ， B D$ ，作 $A E ⊥ B D$ 于点E ．

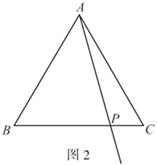(1)、若 $∠ P A C = 10 °$ ，依题意补全图1，并直接写出 $∠ B C D$ 的度数；

(2)、如图2，若 $∠ P A C = α (0 ° < α < 30 °)$ ，
①求证： $∠ B C D = ∠ B A E$ ；

②用等式表示线段 $B D ， C D ， A E$ 之间的数量关系并加以证明．

查看试题解析
27. 如图，已知抛物线 $y = a x^{2} + b x - 3$ 与x轴交于 $A (- 2 ， 0)$ 、 $B (6 ， 0)$ 两点，与y轴交于C点，设抛物线的顶点为D.过点D作 $D E ⊥ x$ 轴，垂足为E.P为线段DE上一动点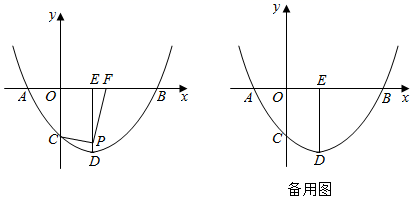， $F (m ， 0)$ 为x轴上一点，且 $P C ⊥ P F$ .

(1)、求抛物线的解析式：

(2)、①当点P与点D重合时，求m的值；
②在①的条件下，将 $△ C O F$ 绕原点按逆时针方向旋转 $90 °$ 并平移，得到 $△ C_{1} O_{1} F_{1}$ ，点C，O，F的对应点分别是点 $C_{1}$ ， $O_{1}$ ， $F_{1}$ ，若 $△ C O F$ 的两个顶点恰好落在抛物线上，直接写出点 $F_{1}$ 的坐标；

(3)、当点P在线段DE上运动时，求m的变化范围.

查看试题解析
28. 在平面直角坐标系xOy中，对于点p和线段ST，我们定义点P关于线段ST的线段比k＝ ${\begin{matrix} \frac{P S}{S T} (P S < P T) \\ \frac{P T}{S T} (P S \geq P T) \end{matrix}$ .

(1)、已知点A（0，1），B（1，0）.
①点Q（2，0）关于线段AB的线段比k＝ ▲ ；

②点C（0，c）关于线段AB的线段比k＝ $\sqrt{2}$ ，求c的值.

(2)、已知点M（m，0），点N（m＋2，0），直线y＝x＋2与坐标轴分别交于E，F两点，若线段EF上存在点使得这一点关于线段MN的线段比k≤ $\frac{1}{4}$ ，直接写出m的取值范围.

查看试题解析