江苏省无锡市惠山区2021年数学中考一模试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、2 B、-2 C、 D、2. 下列运算正确的是( )A、(a3)2=a6 B、2a+3a=5a2 C、a8÷a4=a2 D、a2·a3=a63. 下面4个汽车标识图案不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列四个立体图形中,从正面看到的图形与其他三个不同的是( )A、
4. 下列四个立体图形中,从正面看到的图形与其他三个不同的是( )A、 B、
B、 C、
C、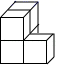 D、
D、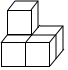 5. 已知圆锥的底面半径为 ,母线长为 ,则这个圆锥的全面积是( )A、 B、 C、 D、6. 现有一数据:3,4,5,5,6,6,6,7,则下列说法正确的是( ).A、众数是5和6 B、众数是5.5 C、中位数是5.5 D、中位数是67. 如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( )
5. 已知圆锥的底面半径为 ,母线长为 ,则这个圆锥的全面积是( )A、 B、 C、 D、6. 现有一数据:3,4,5,5,6,6,6,7,则下列说法正确的是( ).A、众数是5和6 B、众数是5.5 C、中位数是5.5 D、中位数是67. 如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( ) A、40° B、50° C、80° D、100°8. 矩形具有而菱形不一定具有的性质是( )A、两组对边分别平行 B、对角线相等 C、对角线互相垂直 D、对角线平分一组对角9. 如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y= x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为( )
A、40° B、50° C、80° D、100°8. 矩形具有而菱形不一定具有的性质是( )A、两组对边分别平行 B、对角线相等 C、对角线互相垂直 D、对角线平分一组对角9. 如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y= x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为( ) A、3.5 B、2.5 C、2 D、1.210. 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y= (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
A、3.5 B、2.5 C、2 D、1.210. 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y= (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( ) A、5 B、10 C、15 D、20
A、5 B、10 C、15 D、20二、填空题
-
11. 分解因式 .12. 2020年12月9日世卫组织公布,全球新冠肺炎确诊病例超6810万例,请用科学记数法表示6810万例为例.13. 函数中自变量x的取值范围是 .14. 某个函数具有性质:当 时, 随 的增大而增大,这个函数的表达式可以是(只要写出一个符合题意的答案即可).15. 已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为 .16. 如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=100°,则∠A+∠C=.
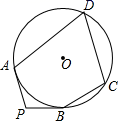 17. 如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中, , ,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.18. 如图,在平行四边形 中, , ,点 为边 上的一个动点,连接 并延长至点 ,使得 ,以 、 为邻边构造平行四边形 ,连接 ,则 的最小值为.
17. 如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中, , ,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.18. 如图,在平行四边形 中, , ,点 为边 上的一个动点,连接 并延长至点 ,使得 ,以 、 为邻边构造平行四边形 ,连接 ,则 的最小值为.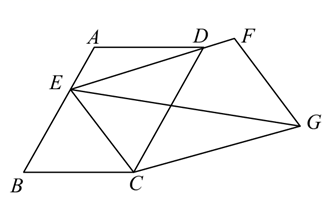
三、解答题
-
19. 计算:(1)、(2)、(2x﹣y)2﹣(x+y)(x﹣y)20.(1)、解方程: ;(2)、解不等式组:21. 已知:如图,点E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF.
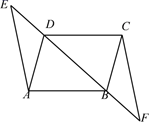
求证:
(1)、AD=BC;(2)、AE∥CF22. 为弘扬中华传统文化,某校开展“汉剧进课堂”的活动,该校随机抽取部分学生,按四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成两幅不完整的统计图,根据图中提供的信息,解决下列问题: (1)、这次共抽取名学生进行统计调查,扇形统计图中,D类所对应的扇形圆心角的大小为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,估计该校表示“喜欢”的B类的学生大约有多少人?23. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.24. 已知在四边形ABCD中, 是 边上一点,且 .分别在图①和图②中用直尺和圆规作出所有满足条件的点 .(保留作图痕迹,不写作法)
(1)、这次共抽取名学生进行统计调查,扇形统计图中,D类所对应的扇形圆心角的大小为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,估计该校表示“喜欢”的B类的学生大约有多少人?23. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.24. 已知在四边形ABCD中, 是 边上一点,且 .分别在图①和图②中用直尺和圆规作出所有满足条件的点 .(保留作图痕迹,不写作法)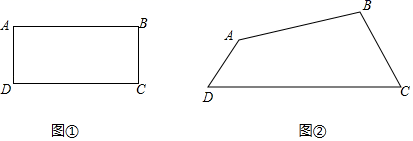 (1)、如图①,四边形 是矩形;(2)、如图②,在四边形 中, .25. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)、如图①,四边形 是矩形;(2)、如图②,在四边形 中, .25. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.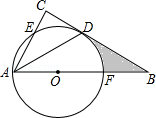 (1)、试判断直线BC与⊙O的位置关系,并说明理由;(2)、若BD=2 ,BF=2,求阴影部分的面积(结果保留π).26. “夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.(1)、求普通床位和高档床位每月收费各多少元?(2)、根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)27. 如图
(1)、试判断直线BC与⊙O的位置关系,并说明理由;(2)、若BD=2 ,BF=2,求阴影部分的面积(结果保留π).26. “夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.(1)、求普通床位和高档床位每月收费各多少元?(2)、根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)27. 如图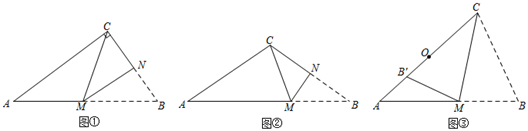
[初步尝试]
(1)、如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为;(2)、[思考说理]如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求 的值;(3)、[拓展延伸]
如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求 的取值范围.
28. 如图,已知二次函数 的图象经过点 ,顶点为 一次函数 的图象交 轴于点 是抛物线上一点,点 关于直线 的对称点 恰好落在抛物线的对称轴直线 上(对称轴直线 与 轴交于点 ).
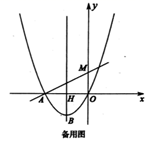 (1)、求二次函数的表达式;(2)、求点 的坐标;(3)、若点 是第二象限内抛物线上一点, 关于抛物线的对称轴的对称点是 ,连接 ,点 是线段 上一点,点 是坐标平面内一点,若四边形 是正方形,求点 的坐标.
(1)、求二次函数的表达式;(2)、求点 的坐标;(3)、若点 是第二象限内抛物线上一点, 关于抛物线的对称轴的对称点是 ,连接 ,点 是线段 上一点,点 是坐标平面内一点,若四边形 是正方形,求点 的坐标.