江苏省南京建邺区2021年数学中考二模试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. 下列计算中,结果最小的是( )A、 B、 C、 D、2. 若 ,则 满足的条件是( )A、 B、 C、 D、3. 在平面直角坐标系 中,下列函数的图象不过点 的是( )A、 B、 C、y=-x+1 D、4. 某校进行环保知识竞赛,进入决赛的共有15 名学生,他们的决赛成绩如下表所示:
决赛成绩/分
100
95
90
85
人数/名
2
8
2
3
则这15名学生决赛成绩的众数和平均数分别是( )
A、95,97 B、95,93 C、95,86 D、90,935. 将边长分别为2和4的长方形如图剪开,拼成一个正方形,则该正方形的边长最接近整数( )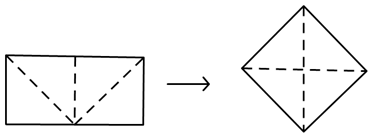 A、1 B、2 C、3 D、46. 如图,在矩形 中, , ,点 在 上,圆 与 相切,与 相交于点 ,则 的长为( )
A、1 B、2 C、3 D、46. 如图,在矩形 中, , ,点 在 上,圆 与 相切,与 相交于点 ,则 的长为( )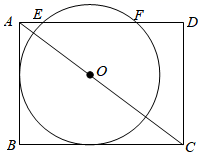 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
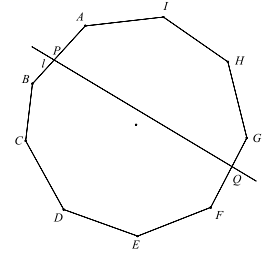
7. 若分式 在实数范围内有意义,则x的取值范围是.8. 2021年5月15日,中国首次火星探测任务天问一号探测器成功在火星乌托邦平原南部预选着陆区着陆.为了探测数据安全有效传回地球,我国 台测控站联网组阵,测控能力更强,能够实现火星距地球最远 公里时的测控通信.用科学记数法表示 是.9. 分解因式: .10. 若 ,则代数式的 值是.11. 若一元二次方程 有实数根,则 的取值范围是.12. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为 斤,一只燕的重量为 斤,则可列方程为 .13. 如图,直线 将正九边形 分为两个区域,且分别与 相交于 点、 点.若 ,则 °.
 14. 已知 与 成反比例,且当 时, ,则 关于 的函数关系式为.15. 如图,在 中, , , ,菱形 顶点 在边 上, 分别在边 上,则 的取值范围是.
14. 已知 与 成反比例,且当 时, ,则 关于 的函数关系式为.15. 如图,在 中, , , ,菱形 顶点 在边 上, 分别在边 上,则 的取值范围是. 16. 已知二次函数 ( 是常数,且 )的图象的对称轴为直线 ,与 轴的一个交点为 ,与 轴的交点在 和 (不包括这两点)之间,则下列结论:① ;②一元二次方程 有两个不相等的实数根;③函数可取得最大值 ;④ .其中所有正确结论的序号是.
16. 已知二次函数 ( 是常数,且 )的图象的对称轴为直线 ,与 轴的一个交点为 ,与 轴的交点在 和 (不包括这两点)之间,则下列结论:① ;②一元二次方程 有两个不相等的实数根;③函数可取得最大值 ;④ .其中所有正确结论的序号是.三、解答题
-
17. 计算:18. 解不等式组:19. 已知 ,求代数式 的值.20. 如图,已知 .

求作: 的内接等边 .
小丽同学的作法及证明过程如下:
作法:①作直径 ;
②作半径 的垂直平分线,垂足为 ,交 于 两点;
③连接 , .
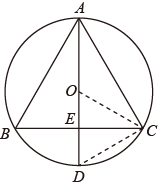
所以 即为 的内接等边三角形.
∵在 中, 垂直平分
∴ ,
∵
∴ (①)
∵
∴ 为等边三角形
∴
∴ (②)
∴ 为 的内接等边三角形.
(1)、在小丽同学的证明过程中,①、②两处的推理依据分别是;.(2)、请你再给出一种作图方法.(尺规作图,保留作图痕迹)21. 为迎接党的百年华诞,某校举办党史知识竞赛,并从中抽取了部分学生的成绩进行统计(满分 分,成绩不低于50分),绘制了如下不完整的统计图表.分数段频数分布表
分数段/分
人数
频率
2
0.04
8
0.16
0.24
24
4
0.08

根据以上信息,完成下列问题:
(1)、本次调查抽取了多少名学生?(2)、求出表中 的值;(3)、将频数分布直方图不全完整;(4)、若甲同学的竞赛成绩是所统计成绩的中位数,则他的成绩落在哪个分数段内?22. 抽屉 中有白袜、黑袜、红袜、蓝袜各 只,抽屉 中有白袜、黑袜各 只,六只袜子除颜色外无其它差别,相同颜色的两只可组成一双袜子.(1)、小明分别从两个抽屉中随机取一只,求组成一双袜子的概率.(2)、小明从抽屉 中取出两只放入抽屉 中,可组成两双袜子的概率是.23. 某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费:月用水量不超过 时,按 元/ 计费;月用水量超过 时,其中 仍按 元/ 收费,超过部分按 元/ 计费,设每户家庭月用水量为 时,应交水费 元.(1)、分别写出 和 时, 与 的函数表达式.(2)、小明家第二季度缴纳水费的情况 如下:月份
四月份
五月份
六月份
交费金额
40元
45元
56.4元
小明家第二季度共用水多少立方米?
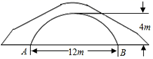
24. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.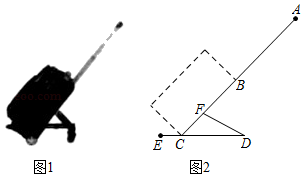 (1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).25. 如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
(1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).25. 如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
 26. 在 中, ,点 在 平分线上,以点 为圆心作 .
26. 在 中, ,点 在 平分线上,以点 为圆心作 . (1)、如图,当 经过点 时,求证: 与直线 相切;(2)、当 同时与直线 相切时,求 的半径.27. (概念学习)
(1)、如图,当 经过点 时,求证: 与直线 相切;(2)、当 同时与直线 相切时,求 的半径.27. (概念学习)在平面直角坐标系 中, 的半径为 ,若 平移 个单位后,使某图形上所有点在 内或 上,则称 的最小值为 对该图形的“最近覆盖距离”.例如,如图①, ,则 对线段 的“最近覆盖距离”为 .

(概念理解)
(1)、 对点 的“最近覆盖距离”为_.(2)、如图②,点 是函数 图象上一点,且 对点 的“最近覆盖距离”为 ,则点 的坐标为_.(3)、如图③,若一次函数 的图象上存在点 ,使 对点 的“最近覆盖距离”为 ,求 的取值范围.(4)、 ,且 ,将 对线段 的“最近覆盖距离”记为 ,则 的取值范围是.