江苏省南通市如皋市2021年数学中考二模试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、-2021 C、 D、2. 新冠肺炎疫情阻击战中,南通是全省唯一主城区没有发本土确诊病例的安全岛.接种新冠疫苗,是巩固抗疫成果最经济、最有效的手段.截止4月24日24时,南通全市已累计接种新冠疫苗102.37万针.其中,102.37万用科学记数法表示为( )A、 B、 C、 D、3. 如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 计算 的结果是( )A、 B、 C、 D、5. 如图,把一块直角三角板的60°角的顶点放在直尺的一边上,如果 ,那么 的度数是( )
4. 计算 的结果是( )A、 B、 C、 D、5. 如图,把一块直角三角板的60°角的顶点放在直尺的一边上,如果 ,那么 的度数是( ) A、35° B、55° C、65° D、75°6. 双曲线 有三个点 , , ,若 ,则 , , 的大小关系是( )A、 B、 C、 D、7. 某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、 “优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( )
A、35° B、55° C、65° D、75°6. 双曲线 有三个点 , , ,若 ,则 , , 的大小关系是( )A、 B、 C、 D、7. 某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、 “优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( ) A、 B、 C、 D、8. 将一个圆锥展开后,其侧面是一个圆心角为108°,半径为12cm的扇形,则该圆锥的底面半径是( )A、1.8cm B、3.6cm C、4cm D、6cm9. 如图1,四边形ABCD中, , , .动点Р从点B出发,沿折线 方向以 单位/秒的速度匀速运动,在整个运动过程中, 的面积S与运动时间t(秒)的函数图象如图2所示,则四边形ABCD的面积是( )
A、 B、 C、 D、8. 将一个圆锥展开后,其侧面是一个圆心角为108°,半径为12cm的扇形,则该圆锥的底面半径是( )A、1.8cm B、3.6cm C、4cm D、6cm9. 如图1,四边形ABCD中, , , .动点Р从点B出发,沿折线 方向以 单位/秒的速度匀速运动,在整个运动过程中, 的面积S与运动时间t(秒)的函数图象如图2所示,则四边形ABCD的面积是( ) A、75 B、80 C、85 D、9010. 如图, 中, , ,垂足为D,P为直线BC上方的一个动点,过点Р作 ,垂足为E,若 ,则 的最小值为( )
A、75 B、80 C、85 D、9010. 如图, 中, , ,垂足为D,P为直线BC上方的一个动点,过点Р作 ,垂足为E,若 ,则 的最小值为( )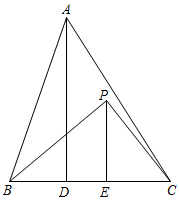 A、4 B、 C、3 D、
A、4 B、 C、3 D、二、填空题
-
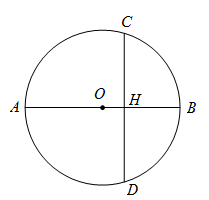
11. 计算: .12. 若分式 有意义,则实数 的取值范围为.13. 如图, 是 的直径,弦 ,垂足为点H.若 , ,则 的半径长为.
 14. 在我国东汉年间编订的数学经典著作《九章算术》中,有这样一个问题:“今有三人公车,二车空;二人公车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,若每3人坐一辆车,则有2辆空车;若每2人坐一辆车,则有9人需要步行,问人与车各多少?设共有 辆车,则可列一元一次方程为.15. 设一元二次方程 的两根分别是 , ,则 .16. 如图,热气球位于观测塔Р的北偏西50°方向,距离观测塔100km的A处,它沿正南方向航行一段时间后,到达位于观测塔Р的南偏西37°方向的B处,这时,B处与观测塔P相距km.(结果保留整数,参考数据: , , , , , )
14. 在我国东汉年间编订的数学经典著作《九章算术》中,有这样一个问题:“今有三人公车,二车空;二人公车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,若每3人坐一辆车,则有2辆空车;若每2人坐一辆车,则有9人需要步行,问人与车各多少?设共有 辆车,则可列一元一次方程为.15. 设一元二次方程 的两根分别是 , ,则 .16. 如图,热气球位于观测塔Р的北偏西50°方向,距离观测塔100km的A处,它沿正南方向航行一段时间后,到达位于观测塔Р的南偏西37°方向的B处,这时,B处与观测塔P相距km.(结果保留整数,参考数据: , , , , , ) 17. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,记 的面积为 ,四边形CDOE的面积为 ,则 .
17. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,记 的面积为 ,四边形CDOE的面积为 ,则 .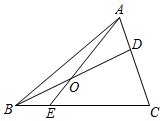 18. 已知抛物线 过点 ,与 轴和直线 分别相交于点A、B,点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,若 ,则b的取值范围为.
18. 已知抛物线 过点 ,与 轴和直线 分别相交于点A、B,点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,若 ,则b的取值范围为.三、解答题
-
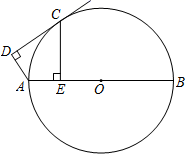
19.(1)、解不等式组 ,并写出其所有整数解;(2)、先化简,再求值: ,其中 .20.(1)、某运输队第一次运输360吨化肥,装载了6节火车车厢和15辆汽车;第二次装载了8节火车车厢和10辆汽车,比第一次多运输了化肥80吨.每节火车车厢与每辆汽车平均各装多少吨化肥?(2)、如图,AB是 的直径,点C在 上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.求证 .
 21. 2021年我省全面推行初中学业水平考试改革,为了解各市九年级学生复习备考情况,省教育厅准备对各市进行一次实地调研活动,调研的对象初步确定从A市、B市、C市、D市、E市中随机抽签选取.(1)、若这次调研准备选取一个市,则恰好抽到A市的概率是 .(2)、若这次调研准备选取两个市,请用列表或画树状图的方法表示出所有可能,并求出所选取的两个市恰好是A市和B市的概率.22. 如图,在平面直角坐标系中,直线 与双曲线 交于A,B两点,已知点A的横坐标为2.
21. 2021年我省全面推行初中学业水平考试改革,为了解各市九年级学生复习备考情况,省教育厅准备对各市进行一次实地调研活动,调研的对象初步确定从A市、B市、C市、D市、E市中随机抽签选取.(1)、若这次调研准备选取一个市,则恰好抽到A市的概率是 .(2)、若这次调研准备选取两个市,请用列表或画树状图的方法表示出所有可能,并求出所选取的两个市恰好是A市和B市的概率.22. 如图,在平面直角坐标系中,直线 与双曲线 交于A,B两点,已知点A的横坐标为2. (1)、求k的值;(2)、求 的面积;(3)、直接写出关于 的不等式 的解集.23. 某校组织学生参加“防疫卫生知识竞赛”(满分为150分),为了了解某班学生在这次竞赛中的表现,现随机抽取该班10名同学的竞赛成绩制表如下:
(1)、求k的值;(2)、求 的面积;(3)、直接写出关于 的不等式 的解集.23. 某校组织学生参加“防疫卫生知识竞赛”(满分为150分),为了了解某班学生在这次竞赛中的表现,现随机抽取该班10名同学的竞赛成绩制表如下:成绩
148
121
90
88
86
85
81
学生数
1
2
1
1
1
3
1
请根据表中信息,解答下列问题:
(1)、这10名学生竞赛成绩的平均数是分,中位数是分;(2)、甲、乙两人分别用样本的平均数和中位数来推断该班全体学生本次竞赛的情况,请你写出甲、乙两人的推断结论;(3)、指出(2)中谁的推断能较为合理地能反映出该班全体学生本次竞赛的真实水平,并说出另一个人的推断不合理的原因.24. 在平面直角坐标系中,A,B分别是直线 ,抛物线 上的动点,其横坐标分别为 , .(1)、点B的纵坐标用含有n的式子可表示为.(2)、连接AB,当 轴,A在B的右侧且 时,求m的值;(3)、当 , 时,作直线AB交y轴于点C,请直接写出C点纵坐标y的取值范围.25. 如图,在矩形ABCD中,P为CD边上一点 ,将 沿AP翻折得到 , 的延长线交边AB于点M,过点B作 交DC于点N.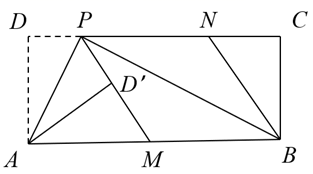 (1)、若 ,
(1)、若 ,①求证 ;
②判断四边形PMBN的形状,并说明理由;
(2)、若 ,求 的值.26. (了解概念)定义:在平面直角坐标系 中,组成图形的各点中,与点Р所连线段最短的点叫做点Р关于这个图形的短距点,这条最短线段的长度叫做点Р到这个图形的短距.

(理解运用)
(1)、已知点 ,以原点为圆心,l为半径作 ,则点Р关于 的短距点的坐标是;(2)、如图,点 ,等边三角形OAB的顶点A的坐标为 ,顶点B在第一象限,判断点Р关于 的短距点的个数,并说明理由;(3)、已知 , , ,点C在第一象限内,且 , ,若点Р到四边形OACB的短距大于2,请直接写出 的取值范围.