江苏省连云港市赣榆区2021年数学中考适应性试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. 9的相反数是( )A、-9 B、9 C、 D、2. 下列图标中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图所示的几何体是由一个球体和一个长方体组成的,它的主视图是( )
3. 如图所示的几何体是由一个球体和一个长方体组成的,它的主视图是( )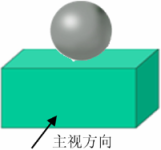 A、
A、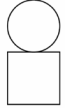 B、
B、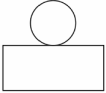 C、
C、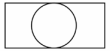 D、
D、 4. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、5. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、6. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、7. 如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
4. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、5. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、6. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、7. 如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )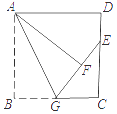 A、1 B、1.5 C、2 D、2.58. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、1 B、1.5 C、2 D、2.58. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、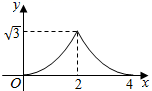 B、
B、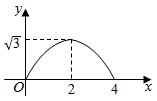 C、
C、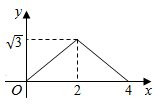 D、
D、
二、填空题
-
9. 2021年1月1日,“学习强国”平台全国上线,截至2021年5月5日,某市党员“学习强国”客户端注册人数约1290000.数据1290000科学记数法表示为.10. 如果单项式3xmy与﹣5x3yn是同类项,那么m+n= .11. 今年某果园随机从甲、乙、丙三个品种的枇杷树中各选了5棵,每棵产量的平均数 (单位:千克)及方差S2(单位:千克2)如表所示:
甲
乙
丙
45
45
42
S2
1.8
2.3
1.8
明年准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是.
12. 正方形网格中,∠AOB如图放置,则tan∠AOB=.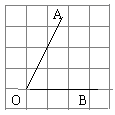 13. 如图,圆锥的母线AB=6,底面半径CB=2,则其侧面展开图扇形的圆心角α=.
13. 如图,圆锥的母线AB=6,底面半径CB=2,则其侧面展开图扇形的圆心角α=.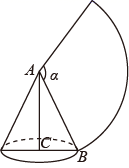 14. 如图,点E、F在反比例函数y= (x>0)的图象上,直线EF分别与x、y轴交于点A、B,且BE:BF=1:3,则S△OEF=.
14. 如图,点E、F在反比例函数y= (x>0)的图象上,直线EF分别与x、y轴交于点A、B,且BE:BF=1:3,则S△OEF=.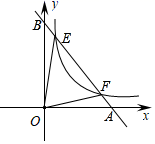 15. 如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段PA绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是.
15. 如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段PA绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是.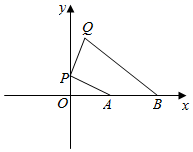
三、解答题
-
16. 计算:(-4)2+(π-3)0-23-|-5|.17. 化简: .18. 解不等式组: .19. 在一个黑色的布口袋里装着白、红、黑三种颜色的小球,它们除了颜色之外没有其它区别,其中白球2只、红球1只、黑球1只.袋中的球已经搅匀.(1)、随机地从袋中摸出1只球,则摸出白球的概率是多少?(2)、随机地从袋中摸出1只球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.20. 某地区在所有中学开展《老师,我想对你说》心灵信箱活动,为师生之间的沟通增设了一个书面交流的渠道.为了解两年来活动开展的情况,某课题组从全地区随机抽取部分中学生进行问卷调查.对“两年来,你通过心灵信箱给老师总共投递过封信?”这一调查项设有四个回答选项,选项A:没有投过;选项B:一封;选项C:两;选项D:三封及以上.根据接受问卷调查学生的回答,统计出各选项的人数以及所占百分比,分别绘制成如下条形统计图和扇形统计图:
 (1)、此次抽样调查了名学生,条形统计图中m= , n=;(2)、请将条形统计图补全;(3)、接受问卷调查的学生在活动中投出的信件总数至少有封;(4)、全地区中学生共有110000名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多少名?21. 如图, 是正方形,E是 边上任意一点,连接 ,作 ,垂足分别为F,G.求证: .
(1)、此次抽样调查了名学生,条形统计图中m= , n=;(2)、请将条形统计图补全;(3)、接受问卷调查的学生在活动中投出的信件总数至少有封;(4)、全地区中学生共有110000名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多少名?21. 如图, 是正方形,E是 边上任意一点,连接 ,作 ,垂足分别为F,G.求证: .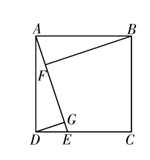 22. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
22. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:x(元)
15
20
30
…
y(袋)
25
20
10
…
若日销售量y是销售价x的一次函数,试求:
(1)、日销售量y(袋)与销售价x(元)的函数关系式;(2)、假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?23. 如图,两座建筑物的水平距离 为 ,从 点测得 点的俯角 为 ,测得 点的俯角 为 .求这两座建筑物 的高度.(结果保留小数点后一位, , .) 24. 如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
24. 如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.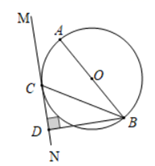 (1)、求证:∠ABC=∠CBD;(2)、若BC=4 ,CD=4,则⊙O的半径是.25. 在 中, . 点 是平面内不与点 重合的任意一点, 连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接
(1)、求证:∠ABC=∠CBD;(2)、若BC=4 ,CD=4,则⊙O的半径是.25. 在 中, . 点 是平面内不与点 重合的任意一点, 连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接
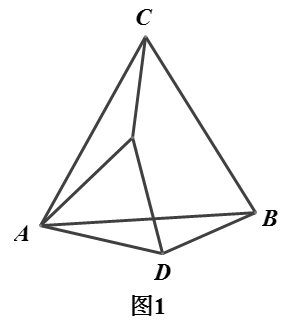 (1)、动手操作
(1)、动手操作如图1,当 时,我们通过用 刻度尺和量角器度量发现:
的值是 ;直线 与直线 相交所成的较小角的度数是 ;
请证明以上结论正确.
(2)、类比探究如图2,当 时,请写出 的值及直线 与直线 相交所成的较小角的度数,并就图2的情形说明理由.
 26. 如图,在平面直角坐标系中,直线 与x轴交于点 ,与 轴交于点 ,抛物线 经过 两点且与x轴的负半轴交于点 .
26. 如图,在平面直角坐标系中,直线 与x轴交于点 ,与 轴交于点 ,抛物线 经过 两点且与x轴的负半轴交于点 .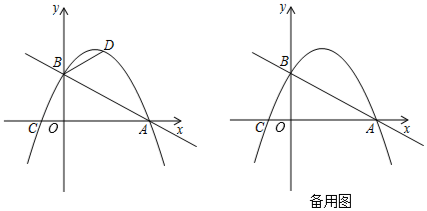 (1)、求该抛物线的解析式;(2)、若点 为直线 上方抛物线上的一个动点,当 时,求点 的坐标;(3)、已知 分别是直线 和抛物线上的动点,当 为顶点的四边形是平行四边形时,直接写出所有符合条件的 点的坐标.
(1)、求该抛物线的解析式;(2)、若点 为直线 上方抛物线上的一个动点,当 时,求点 的坐标;(3)、已知 分别是直线 和抛物线上的动点,当 为顶点的四边形是平行四边形时,直接写出所有符合条件的 点的坐标.