江苏省淮安市洪泽区2021年数学中考二模试卷
试卷更新日期：2021-09-28 类型：中考模拟
一、单选题
-
1. －3的相反数是（ ）A、－3 B、3 C、±3 D、2. 已知某细菌直径为0.0000025米，则0.0000025用科学记数法可表示为（ ）A、250×10﹣8 B、25×10﹣7 C、2.5×10﹣6 D、0.25×10﹣53. 实验中学选择10名青少年志愿者参加读书日活动，年龄如表所示：这10名志愿者年龄的众数和中位数分别是（ ）
年龄
12
13
14
15
人数
2
3
4
1
A、14，13 B、14，14 C、14，13.5 D、13，144. 如图是由5个相同的小正方体组成的立体图形，它的左视图是（ ）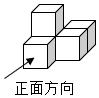
A、
B、
C、
D、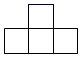
5. 如图，AB∥CD，AF交CD于点E，且BE⊥AF，∠AEC＝40°，则∠B为（ ）°
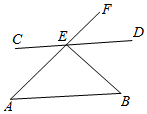A、40 B、50 C、130 D、1406. 如图，在边长为1的正方形网格中，以AB为直径的圆过C、D两点，则tan∠BCD的值为（ ）
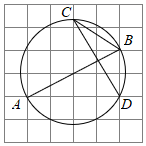A、 B、 C、 D、27. 如图，在数轴上表示 的点在哪两个字母之间（ ）
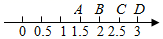A、A与B B、B与C C、A与C D、C与D8. 代数式：x﹣3x2+5x3﹣7x4+9x5+…的第n项为（ ）A、（﹣1）n﹣1（2n﹣1）xn B、（﹣1）n（2n﹣1）xn C、（﹣1）n﹣1（2n+1）xn D、（﹣1）n﹣1nxn二、填空题
-
9. 分解因式：x2﹣xy= ．
10. 已知一组数据：1，3，a，8，10的平均数是5，则a＝.11. 点A在反比例函数y＝ 图象上，且位于第二象限，过点A作AB⊥y轴于点B，已知△ABO面积为3，则k的值是.12. 已知圆锥的母线长为5，底面圆半径为3，则此圆锥的侧面积为.（结果保留 ）13. 如图，l1∥l2∥l3 ， AC交l1、l2、l3分别于A、B、C，且AC＝6，BC＝4，DF交l1、l2、l3分别于D、E、F，则 ＝.
14. 如图，一副三角板按图示放置，已知∠AOC＝65°，则∠AOB＝°.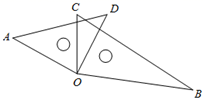
15. 抛物线y＝x2﹣2x+a顶点在x轴上，则a＝.16. 将2021个边长为1的正方形按如图所示的方式排列，点A，A1 ， A2 ， A3 ， …，A2021和点M，M1 ， M2 ， …，M2020是正方形的顶点，连接AM1 ， AM2 ， AM3 ， …，AM2020 ， 分别交正方形的边A1M，A2M1 ， A3M2 ， …，A2020M2019于点N1 ， N2 ， N3 ， …，N2020 ， 则N2020A2020长为.
三、解答题
-
17. 计算：(1)、（﹣2）3+| ﹣5|+9×3﹣1.(2)、解方程组： .18. 先化简代数式：（x﹣ ）÷ ，再求当x＝﹣3时代数式的值.19. 为改善生态环境、防止水土流失，3月12日，某单位积极响应中央号召，组织后勤和信息两个部门职工到山村荒坡上植树.已知这天后勤部门种植了1500棵树，信息部门种了1000棵树，后勤部门职工比信息部门多10人，假设每人种树棵数相同，问该单位信息部门有多少人参加植树？20. 如图，线段AC交BD于O，点E，F在线段AC上，△DFO≌△BEO，且AF＝CE，连接AB、CD，求证：AB＝CD．
21. 为了解某校九年级320名男生体育中考的成绩情况，从中随机抽取部分男生进行测试，并把测试成绩分为A、B、C、D四个等次，绘制成如图所示的不完整的统计图，请你依图回答下列问题.
(1)、a＝ ， b＝ ， c＝；(2)、若成绩达到C、D即为优秀，估计该校男生体育成绩优秀人数.22. 一个不透明的布袋中装有标着数字2，3，6的三张卡片，从中任意抽取一张，用上面的数字做十位数，放回后，再抽取一张，用上面的数字做个位数，请用树状图或列表方法，求两次抽出的数字组成的数是4的倍数的概率.23. 小君学习了解直角三角形知识，周末带着测角仪和同学一起去测量当地一座宝塔CD的高度，由于自然环境限制，他们选定距离宝塔若干米的A处，测得塔顶C的仰角为27°，然后沿着正对塔底的方向前进50米到达B处，在此又测得塔顶C的仰角为45°.如果测角仪的高度忽略不计，那么这座宝塔高度是多少？（tan27°≈0.51，sin27°≈0.45，cos27°≈0.89，结果精确到1米）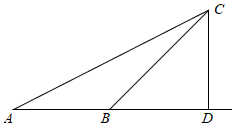
24. 李师傅开着货车从甲地出发匀速驶往距离甲地360千米的乙地，一段时间后，王东开着一辆轿车从乙地出发沿同一条道路匀速驶往甲地.两人在距离乙地160千米处相遇，此后2小时各自到达自己的目的地.图中线段AB表示李师傅离乙地距离y1（千米）与他出发时间x（小时）的函数关系，根据以上条件回答下列问题：
(1)、李师傅的货车速度为千米/小时；王东在李师傅出发小时后才出发；(2)、求y1与x之间的函数表达式；(3)、请在图中画出王东离开乙地的距离y2与x之间的函数图象；该函数图象交AB于点C，请写出点C坐标，并解释其实际意义.25. 如图，已知AB是⊙O的弦，C为⊙O上一点，AD是⊙O的切线.
(1)、求证：∠C＝∠BAD；(2)、若BD⊥AB于点B，AD＝9，BD＝6，求⊙O半径.26. 在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，得到△BFE.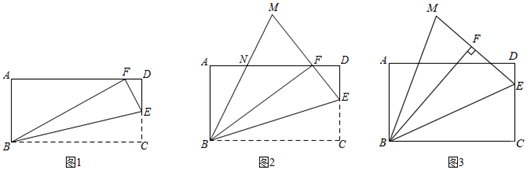
(1)、点F恰好在AD上；①如图1，若∠FEB＝75°，求出AB：BC的值.
②如图2，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF＝ BC时，求出AB：BC的值.
(2)、E从C到D的运动过程中.①如图3，若AB＝5，BC＝8，∠ABF的角平分线交EF的延长线于点M，求M到AD的距离；
②在①的条件下，E从C到D的过程中，直接写出M运动的路径长.
27. 在平面直角坐标系xOy中，二次函数y＝ax2+bx的图象与x轴交于O、A两点，其顶点B的坐标为（2，﹣6）.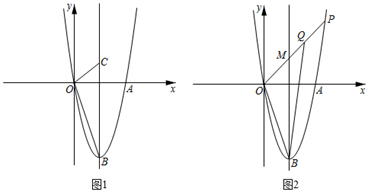
(1)、求a、b的值；(2)、如图1，点C是该二次函数图象的对称轴上的一个动点，连接BO、CO，当△OBC是以BC为腰的等腰三角形时，求点C的坐标；(3)、如图2，P是该二次函数图象上的位于第一象限内的一个动点，连接OP，与对称轴交于点M，点Q在OP上，满足 ＝ ，设点P的横坐标为n；①请用含n的代数式表示点Q的坐标（，）；
②连接BQ，OB，当△OBQ的面积为15时，求点P的坐标；
③当∠POA＝2∠OBM时，直接写出点P的横坐标.