湖南省益阳市赫山区2021年数学中考三模试卷

试卷更新日期：2021-09-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算3⁰的结果是（）

A、3 B、30 C、1 D、0

查看试题解析
2. 如图，∠1+∠2等于（）

A、60° B、90° C、110° D、180°

查看试题解析
3. 下列分解因式正确的是（）

A、 $- a + a^{3} = - a (1 + a^{2})$ B、 $2 a - 4 b + 2 = 2 (a - 2 b)$ C、 $a^{2} - 4 = {(a - 2)}^{2}$ D、 $a^{2} - 2 a + 1 = {(a - 1)}^{2}$

查看试题解析
4. 下列运算中，正确的是（）

A、2x－x=1 B、x＋x⁴=x⁵ C、(－2x)³=－6x³ D、x²y÷y=x²

查看试题解析
5. 一次函数y=6x+1的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，点P在反比例函数 $y = \frac{3}{x}$ 的图象上，且横坐标为1，过点P作两条坐标轴的平行线，分别与x轴、y轴交于A、B两点，则直线AB与x轴所夹锐角的正切值为（）

A、3 B、 $\frac{1}{3}$ C、﹣3 D、﹣ $\frac{1}{3}$

查看试题解析
7. 甲、乙、丙三个旅行团的游客人数都相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方差分别是S_甲²＝27，S_乙²＝19.6，S_丙²＝1.6，导游小王最喜欢带游客年龄相近的团队，若在三个团中选择一个，则他应选（）

A、甲团 B、乙团 C、丙团 D、甲或乙团

查看试题解析
8. 一小球被抛出后，距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式：h＝－5(t－1)²＋6，则小球距离地面的最大高度是（）

A、1米 B、5米 C、6米 D、7米

查看试题解析
9.
如图，在△ABC 中，∠C=90°，BC=6，D，E 分别在 AB、AC上，将△ABC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为（　　）

A、 $\frac{1}{2}$ B、2 C、3 D、4

查看试题解析
10.
如图，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y和x，则y与x的函数图象大致是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. $\sqrt[3]{5}$ ，π，－4，0这四个数中，最大的数是.

查看试题解析
12. 如图，已知菱形ABCD，其顶点A、B在数轴上对应的数分别为－4和1，则BC=

查看试题解析
13. 若|x﹣3|+|y+2|＝0，则x+y的值为.

查看试题解析
14. 如图，点O为优弧ACB所在圆的心，∠AOC=108°，点D在AB的延长线上，BD=BC，则∠D=.

查看试题解析
15. 如图8中图①，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②，则阴影部分的周长为.

查看试题解析
16. 计算： $\sqrt{27} - \sqrt{\frac{1}{3}} =$ .

查看试题解析
17. 如图，给正五边形的顶点依次编号为1、2、3、4、5，若从某一顶点开始，沿五边形的边顺时针行走，顶点编号是几，就走几个边长，则称这种走法为一次“移位”. 如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→l为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”，则他所处顶点的编号为.

查看试题解析
18. 二次函数y＝ax²+bx+c（a≠0）的图象如图，给出下列结论：①4ac﹣b²＜0；②4a+c＜2b；③b﹣2a=0；其中正确结论是（填序号）.

查看试题解析

三、解答题

19. 计算：（π﹣3.14）⁰+ $\sqrt{9}$ +（﹣1）²⁰²⁰﹣（﹣ $\frac{1}{2}$ ）^﹣1.

查看试题解析
20. 先化简，再求值： $(\frac{x - 1}{x^{2} - 1} + \frac{1}{x + 1}) \div \frac{4}{x^{2} + x}$ ，其中x=﹣2.

查看试题解析
21. 如图，在 $△ A B C$ 中， $D$ 为 $B C$ 上一点， $∠ B A D = ∠ C$ .

(1)、求证： $△ A B D ∽ △ C B A$ .

(2)、若 $A B = 6 ， B D = 3$ ，求 $C D$ 的长.

查看试题解析
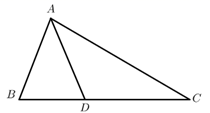22. 甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.
⑴问乙单独整理多少分钟完工？

查看试题解析
23. 2011年5月31日是第24 个世界无烟日，也是我国从5月1日开始在公共场所禁止吸烟满一个月的日子.为创建国家级卫生城市，搞好公共场所卫生管理，市育才实验学校九年级(1)班社会实践小组对某社区居民开展了“你支持哪种戒烟方式”的问卷调查，图9是根据调查结果绘制的两幅不完整的统计图.

请根据以上条形统计图和扇形统计图提供的信息，解答下列问题：

(1)、九年级(1)班社会实践小组一共调查了名社区居民.

(2)、扇形统计图中，表示支持“替代品戒烟”的扇形的圆心角的度数为.

(3)、请将条形统计图补充完整.

查看试题解析
24. 为发展旅游经济，我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人，非节假日打a折售票，节假日按团队人数分段定价售票，即m人以下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人部分的游客打b折售票.设某旅游团人数为x人，非节假日购票款为y₁（元），节假日购票款为y₂（元）.y₁与y₂之间的函数图象如图所示.

(1)、观察图象可知：a＝；b＝；m＝；

(2)、求出y₁ ， y₂与x之间的函数关系式.

查看试题解析
25. 如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE＝BK＝AG.

(1)、求证：①DE＝DG；
②DE⊥DG；

(2)、以线段DE，DG为边作出正方形DEFG，连接KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；

(3)、当 $\frac{C E}{C B} = \frac{1}{n}$ 时，请写出 $\frac{S_{A B C D}}{S_{D E F G}}$ 的值，并说明理由.

查看试题解析
26. 如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x²＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.

(1)、求c、b（用含t的代数式表示）；

(2)、当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.
①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；

②求△MPN的面积S与t的函数关系式，并求t为何值时，S= $\frac{21}{8}$ ；

③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围.

查看试题解析