湖北省荆州市沙市区2021年数学中考三模试卷

试卷更新日期：2021-09-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 在下列四个实数中，最小的是（）

A、﹣2 B、﹣ $\sqrt{3}$ C、0 D、 $\frac{1}{4}$

查看试题解析
2. 下列计算正确的是（）

A、2a＋3a＝5a² B、（a²）³＝a⁵ C、﹣8a²÷4a＝2a D、2 $\sqrt{a}$ ×3 $\sqrt{b}$ ＝6 $\sqrt{a b}$

查看试题解析
3. 为了将“新冠“疫情对国民经济的影响降至最低，中国政府采取积极的财政税收政策，切实减轻企业负担，以促进我国进出口企业平稳发展.据国家统计局相关数据显示，2020年1月至5月，全国累计办理出口退税632400000000元，其中数字632400000000用科学记数法表示为（）

A、6.324×10¹¹ B、6.324×10¹⁰ C、632.4×10⁹ D、0.6324×10¹³

查看试题解析
4. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，直线l_l∥l₂ ，直角三角板的直角顶点C在直线l₁上，一锐角顶点B在直线l₂上，若∠1=35°，则∠2的度数是

A、65° B、55° C、45° D、35°

查看试题解析
6. 如图是三种化合物的结构式及分子式，则按其规律第9个化合物的分子式为（）

A、C₈H₁₆ B、C₈H₁₈ C、C₉H₁₈ D、C₉H₂₀

查看试题解析
7. 甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示，如果从这四位同学中，选出一位同学参加数学竞赛，那么应选___________去.

甲

乙

丙

丁

平均分

85

90

90

85

方差

50

42

50

42

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图，王虎使一长为4cm，宽为3cm的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为A→A₁→A₂ ，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（）

A、10cm B、4πcm C、 $\frac{7}{2} π cm$ D、 $\frac{5}{2} cm$

查看试题解析
9. 美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感.如图，某女士身高165cm，下半身长x与身高l的比值是0.60，为尽可能达到美的效果，她应穿的高跟鞋的高度大约为（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
10. 定义（a，b，c）为方程 $a x^{2} + b x + c = 0$ 的特征数.若特征数为（ $k^{2}$ ， $- 1 - 2 k$ ，1）的一元二次方程有两个实数根，则k的取值范围是（）

A、 $k$ ＜ $- \frac{1}{4}$ B、k ＞ $- \frac{1}{4}$ C、k ＞ $- \frac{1}{4}$ 且 $k \neq 0$ D、k≥ $- \frac{1}{4}$ 且 $k \neq 0$

查看试题解析

二、填空题

11. 已知方程组 ${\begin{matrix} 3 x - 2 y = 1 \\ 2 x - 3 y = - 1 \end{matrix}$ ，则x＋y的值为.

查看试题解析
12. 计算|﹣6|﹣（π﹣ $\sqrt{3}$ ）⁰﹣ $\sqrt{9}$ ﹣（ $\frac{1}{2}$ ）^﹣2的结果为.

查看试题解析
13. 如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，BC、AB长为半径画弧，两孤交于点D，分别连结AB、AD、CD.则四边形ABCD是平行四边形，其依据是.

查看试题解析
14. 如图，无人机在空中C处测得地面A、B两点的俯角分别为60°、45°，如果无人机距地面高度CD为 $100 \sqrt{3}$ 米，点A、D、B在同一水平直线上，则A、B两点间的距离是米.（结果保留根号）

查看试题解析
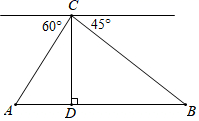15. 如图，在三角形ABC中，∠BAC＝90°，AC＝12，AB＝10，D是AC上一动点，以AD为直径的⊙O交BD于点E，则线段CE的最小值是.

查看试题解析
16. 如图，直线y＝﹣x＋m与双曲线y＝﹣ $\frac{2}{x}$ 相交于A，B两点BC∥x轴，AC∥y轴，则△ABC面积的最小值为.

查看试题解析

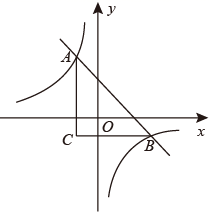
三、解答题

17. 先将代数式 $\frac{x + 1}{x^{2} - 4}$ ×（ $\frac{1}{x + 1}$ ＋1）化简，再从不等式组 ${\begin{matrix} x + 1 \geq 0 \\ 5 - 2 x > 3 \end{matrix}$ 的解集中选一个合适的整数x代入求值.

查看试题解析
18. 小颖利用平方差公式，自己探究出一种解某一类根式方程的方法.下面是她解方程 $\sqrt{x - 2}$ ＋ $\sqrt{x - 7}$ ＝5的过程.
解：设 $\sqrt{x - 2}$ ﹣ $\sqrt{x - 7}$ ＝m，与原方程相乘得：

（ $\sqrt{x - 2}$ ＋ $\sqrt{x - 7}$ ）×（ $\sqrt{x - 2} - \sqrt{x - 7}$ ）＝5m，

x﹣2﹣（x﹣7）＝5m，解之得m＝1，

∴ $\sqrt{x - 2}$ ﹣ $\sqrt{x - 7}$ ＝1，与原方程相加得：

（ $\sqrt{x - 2}$ ＋ $\sqrt{x - 7}$ ）+（ $\sqrt{x - 2} - \sqrt{x - 7}$ ）＝5＋1，

2 $\sqrt{x - 2}$ ＝6，解之得，x＝11，经检验，x＝11是原方程的根.

学习借鉴解法，解方程 $\sqrt{x - 3}$ ﹣ $\sqrt{x - 6}$ ＝1.

查看试题解析
19. 为推进“传统文化进校园”活动，某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图（每人只能选择一个小组）：

(1)、报名参加课外活动小组的学生共有 ▲ 人，将条形图补充完整；

(2)、扇形图中m= ， n=；

(3)、根据报名情况，学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组，甲、乙恰好都被安排到“地方戏曲”小组的概率是多少？请用列表或画树状图的方法说明.

查看试题解析
20. 在如图所示的平面直角坐标系中，△ABC的顶点坐标分别为A（0，3），B（1，0），C（3，2），仅用无刻度的直尺在给出的网格中画图（画图用实线表示），并回答题目中的问题

(1)、在图1中画出△ABC关于点D成中心对称的图形；

(2)、在图2中作出△ABC的外接圆的圆心M（保留作图痕迹）；

(3)、△ABC外接圆的圆心M的坐标为.

查看试题解析
21. 某数学兴趣小组在探究函数y＝x²﹣2|x|＋3的图象和性质时，经历了以下探究过程；

(1)、研究函数特点：
该小组认为，可以将该函数转化为已经学过的二次函数来研究，即将绝对值符号去掉，得到分段函数（每段均为二次函数），其解析式为y＝x²﹣2|x|＋3＝.（填空）：

(2)、画图象：
在给出的坐标系中，分别画出当x≥0时和x＜0时所对应的二次函数的图象：（要求描出横坐标分别为﹣3，﹣2，﹣1，0.1，2，3所对应的点）

(3)、研究性质：
①观察函数y＝x²﹣2|x|＋3的图象，以下说法正确的有（填写正确的序号）
A.对称轴是直线x＝1

B.函数y＝x²﹣2|x|＋3的图象有两个最低点，其坐标分别是（﹣1，2）、（1，2）

C.当﹣1＜x＜1时，y随x的增大而增大

D.当函数y＝x²﹣2|x|＋3的图象向下平移3个单位长度时，图象与x轴有三个公共点.

②结合图象探究发现，当m满足时，方程x²﹣2|x|＋3＝m有四个解；

③设函数y＝x²﹣2|x|＋3的图象与其对称轴相交于P点，当直线y＝n和函数y＝x²﹣2|x|＋3图象只有两个交点时，且这两个交点与点P所构成的三角形是等腰直角三角形，则n的值为.

查看试题解析
22. 第二十四届冬季奥林匹克运动会将于2022年在北京举办，近些年来冰雪运动得到了蓬勃发展，一个滑雪者从山坡滑下，为了得出滑行距离（单位：m）与滑行时间t（单位：s）之间的关系式，测得一组数据（如表）.

滑行时间t/s 0 1 2 3 4

滑行距离s/m 0 4.5 14 28.5 48

(1)、为观察s与t之间的关系，建立坐标系，以t为横坐标，s为纵坐标.如图所示，描出表中数据对应的5个点，并用平滑的曲线连接它们；

(2)、观察图象，可以看出这条曲线像是我们学过的哪种函数的图象的一部分？请你用该函数模型来近似地表示s与t之间的关系；

(3)、如果该滑雪者滑行了2310m，请你用（2）中的函数模型推测他滑行的时间是多少秒.（结果要化简）.

查看试题解析
23. 在矩形ABCD中，E为DC边上一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F.

(1)、求证：△ABF∽△FCE；

(2)、若AB＝8，AD＝10，求EC的长；

(3)、在（2）的条件下，连接BE，求sin∠AEB的值.

查看试题解析
24.
如图，已知抛物线与x轴交于点A（2，0），点B与y轴交于点C（0，2），其对称轴为直线l：x＝4
.

(1)、求抛物线的解析式及点B的坐标；

(2)、在直线l上是否存在一点P，使AP＋CP的值最小？若存在，求AP＋CP的最小值；若不存在，请说明理由；

(3)、以AB为直径作⊙M，在直线l上是否存在点Q，使得过点Q作⊙M的切线QE（E为切点）恰好过点C？若存在，求切线QE的解析式；若不存在，说明理由.

查看试题解析

	甲	乙	丙	丁
平均分	85	90	90	85
方差	50	42	50	42

滑行时间t/s	0	1	2	3	4
滑行距离s/m	0	4.5	14	28.5	48