湖北省汉川市2021年数学第二次学业水平调研考试试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. 如图,直线 ,将一块含30°角的直角三角尺按图中方式放置,其中点A和点B两点分别落在直线a和b上.若∠2=40°,则∠1的度数为( )
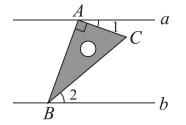 A、20° B、30° C、40° D、60°2. 2020年7月23日,中国首颗火星探测器“天问一号”顺利升空,当“天问一号”探测器抵达火星附近时,总飞行里程将达到470000000公里.将数470000000用科学记数法表示正确的是( )A、 B、 C、 D、3. 下图是某个几何体的展开图,该几何体是( )
A、20° B、30° C、40° D、60°2. 2020年7月23日,中国首颗火星探测器“天问一号”顺利升空,当“天问一号”探测器抵达火星附近时,总飞行里程将达到470000000公里.将数470000000用科学记数法表示正确的是( )A、 B、 C、 D、3. 下图是某个几何体的展开图,该几何体是( ) A、三棱柱 B、三棱锥 C、圆柱 D、圆锥4. 下列运算中正确的是( )A、 B、 C、 D、5. 2019年第七届世界军人运动会(7 th CISM Military World Games)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在赛前训练中射击了10次成绩如图所示.下列结论中错误的是( )
A、三棱柱 B、三棱锥 C、圆柱 D、圆锥4. 下列运算中正确的是( )A、 B、 C、 D、5. 2019年第七届世界军人运动会(7 th CISM Military World Games)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在赛前训练中射击了10次成绩如图所示.下列结论中错误的是( ) A、众数是8 B、中位数是8 C、平均数是8.2 D、方差1.66. 如图,正方形 的边长为1,中心为点O,有一边长大小不定的正六边形 绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形 内(包括正方形的边),当这个六边形的边长最大时, 的最小值为( )
A、众数是8 B、中位数是8 C、平均数是8.2 D、方差1.66. 如图,正方形 的边长为1,中心为点O,有一边长大小不定的正六边形 绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形 内(包括正方形的边),当这个六边形的边长最大时, 的最小值为( ) A、 B、 C、 D、7. 如图,在 中, , , 于点D.点 从点A出发,沿 的路径运动,运动到点C停止,过点 作 于点E,作 于点F.设点P运动的路程为x,四边形 的面积为y,则能反映y与x之间函数关系的图象是( )
A、 B、 C、 D、7. 如图,在 中, , , 于点D.点 从点A出发,沿 的路径运动,运动到点C停止,过点 作 于点E,作 于点F.设点P运动的路程为x,四边形 的面积为y,则能反映y与x之间函数关系的图象是( ) A、
A、 B、
B、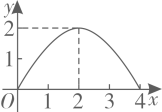 C、
C、 D、
D、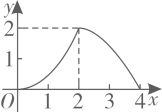
二、填空题
-
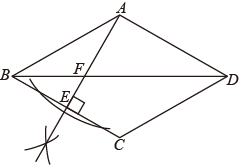
8. 式子 中x的取值范围是.9. 已知一元二次方程 的两实数根为 和 ,则 的值为 .10. 已知 ,且 ,则k的值为.11. 如图, 为菱形 的对角线,作 于点E,交 于点F.若E为 的中点,则 的值是.
 12. 某校组织了主题为“经典诵读”的小视频征集活动,现从中随机抽取部分作品.按 、 、 、 四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.若该校共征集到800份作品,请估计等级为 的作品约有份.
12. 某校组织了主题为“经典诵读”的小视频征集活动,现从中随机抽取部分作品.按 、 、 、 四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.若该校共征集到800份作品,请估计等级为 的作品约有份. 13. 如图,睿智数学兴趣小组为了测量河对岸 的两棵古树A、B之间的距离,他们在河对边沿着与 平行的直线 上取C、D两点,测得 , ,若 , 之间的距离 为50m,则古树A、B之间的距离为m.(结果保留根号)
13. 如图,睿智数学兴趣小组为了测量河对岸 的两棵古树A、B之间的距离,他们在河对边沿着与 平行的直线 上取C、D两点,测得 , ,若 , 之间的距离 为50m,则古树A、B之间的距离为m.(结果保留根号)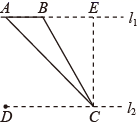 14. 古希腊著名的毕达哥拉斯学派把1、3、6、10、…,这样的数称为“三角形数”,而把1、4、9、16、…,这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.则第10个图形中右下方的“三角形数”中的所有点数是.
14. 古希腊著名的毕达哥拉斯学派把1、3、6、10、…,这样的数称为“三角形数”,而把1、4、9、16、…,这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.则第10个图形中右下方的“三角形数”中的所有点数是. 15. 如图,将矩形纸片 ( )折叠,使点C刚好落在线段 上,且折痕分别与边 , 相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边 , 相交于点E,F.若 , ,则线段 的最大值与最小值的和是.
15. 如图,将矩形纸片 ( )折叠,使点C刚好落在线段 上,且折痕分别与边 , 相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边 , 相交于点E,F.若 , ,则线段 的最大值与最小值的和是.
三、解答题
-
16. 计算:17. 小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
 (1)、若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;(2)、若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同时时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)18. 已知点 、 在某个反比例函数的图象上.(1)、求此反比例函数的解析式;(2)、若直线 与线段AB相交,求m的取值范围.19. “绿水青山就是金山银山”,某村为了绿化荒山,计划在植树节当天种植柏树和杉树.经调查,购买1棵柏树比1棵杉树多50元,且花费900元购买杉树与花费1200元购买柏树的数量相同.(1)、求柏树和杉树的单价各是多少元;(2)、本次绿化荒山,需购买柏树和杉树共80棵,且柏树的棵数不少于杉树的2倍.为完成这次绿化任务,村里筹措了资金15000元,问该村完成这次绿化任务有几种方案?20. 如图,在 中, ,以 为直径作 交 于点D,过点D作 的切线,交 于点E,交 的延长线于点F.
(1)、若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;(2)、若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同时时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)18. 已知点 、 在某个反比例函数的图象上.(1)、求此反比例函数的解析式;(2)、若直线 与线段AB相交,求m的取值范围.19. “绿水青山就是金山银山”,某村为了绿化荒山,计划在植树节当天种植柏树和杉树.经调查,购买1棵柏树比1棵杉树多50元,且花费900元购买杉树与花费1200元购买柏树的数量相同.(1)、求柏树和杉树的单价各是多少元;(2)、本次绿化荒山,需购买柏树和杉树共80棵,且柏树的棵数不少于杉树的2倍.为完成这次绿化任务,村里筹措了资金15000元,问该村完成这次绿化任务有几种方案?20. 如图,在 中, ,以 为直径作 交 于点D,过点D作 的切线,交 于点E,交 的延长线于点F. (1)、求证: ;(2)、当 , 时,求 的长.21. 汈汊湖素有鱼米之乡的美誉,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m( ),销售单价为y元/ .根据以往经验可知:m与t的函数关系为 ;y与t的函数关系如图所示.
(1)、求证: ;(2)、当 , 时,求 的长.21. 汈汊湖素有鱼米之乡的美誉,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m( ),销售单价为y元/ .根据以往经验可知:m与t的函数关系为 ;y与t的函数关系如图所示. (1)、分别求出当 和 时,y与t的函数关系式;(2)、设将这批淡水鱼放养t天后一次性出售所得利润为w元,求当t为何值时,w最大?并求出最大值.(利润=销售总额-总成本)22. 如图, 和 均为等腰三角形, , ,点A,D,E在同一直线上,连接 .
(1)、分别求出当 和 时,y与t的函数关系式;(2)、设将这批淡水鱼放养t天后一次性出售所得利润为w元,求当t为何值时,w最大?并求出最大值.(利润=销售总额-总成本)22. 如图, 和 均为等腰三角形, , ,点A,D,E在同一直线上,连接 . (1)、如图1,若 .
(1)、如图1,若 .①求证: ;
②则 的度数为 ▲ .
(2)、如图2,若 , 为 中 边上的高,试猜想 , , 之间的数量关系,并简要证明你的结论.23. 如图,在平面直角坐标系 中,抛物线 与x轴交于A、B两点(点A在点B的左侧),经过点A的直线 与y轴负半轴交于点C,与抛物线交于另一点D. (1)、则点D的坐标为(用含a的式子表示);(2)、点E是直线l上方的抛物线上的动点,若 面积的最大值为 ,求a的值;(3)、设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A、D、P、Q为顶点的四边形成为矩形时,求出点P的坐标.
(1)、则点D的坐标为(用含a的式子表示);(2)、点E是直线l上方的抛物线上的动点,若 面积的最大值为 ,求a的值;(3)、设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A、D、P、Q为顶点的四边形成为矩形时,求出点P的坐标.