河南省商丘市永城市2021年数学中考二模试卷

试卷更新日期：2021-09-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 中国人最早使用负数，可追溯到两千多年前的秦汉时期， $- 2021$ 的相反数是（）

A、-2021 B、2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 近日.中国通信研究院发布：2021年1－3月份国内市场手机出货量高达9797.3万台.将数据9797.3万用科学记数法表示为（）

A、 $979.73 \times 10^{2}$ B、 $9.7973 \times 10^{3}$ C、 $9.7973 \times 10^{6}$ D、 $9.7973 \times 10^{7}$

查看试题解析
3. 下列运算正确的是（）

A、 $m^{6} \div m^{2} = m^{3}$ B、 ${(m - 1)}^{2} = m^{2} - 1$ C、 ${(m n^{2})}^{3} = m^{3} n^{6}$ D、 $(m - 2) (m + 2) = 4 - m^{2}$

查看试题解析
4. 如图是由10个大小完全相同的小正方体搭成的几何体的俯视图，小正方体上的数字为对应位置上小正方体的数量，将数字“3”上的小正方体向数字“2”上的位置平移一个，下面说法正确的是（）

A、主视图与俯视图不变 B、左视图与俯视图不变 C、主视图与左视图改变 D、三种视图都不变

查看试题解析
5. 李老师在上课途中不小心将一副三角板掉落在地上，直角顶点刚好落在瓷砖的边线上.如图，已知直线 $m / / n$ ，若 $∠ 1 = 35 °$ .则 $∠ 2$ 的度数为（）

A、120° B、122° C、125° D、130°

查看试题解析
6. 某校举办了“口语交际"比赛，五位评委对参赛选手小林的打分依次如下：92，90，93，92，95.对该组数据的说法不正确的是（）

A、平均数为92.4 B、中位数为92 C、众数为92 D、方差为0

查看试题解析
7. 若点 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (3 ， 1)$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，则（）

A、 $y_{1} < 1 < y_{2}$ B、 $y_{1} < y_{2} < 1$ C、 $1 < y_{2} < y_{1}$ D、 $y_{2} < y_{1} < 1$

查看试题解析
8. 关于 $x$ 的一元二次方程 $x^{2} - (p + 2) x + 2 p = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、无实数根

查看试题解析
9. 如图，在边长为2的菱形ABCD中，按如下步骤作图：①分别以点B和点C为圆心，大于 $\frac{1}{2} B C$ 的长为半径画弧.两弧交于点M，N；②作直线MN，且MN恰好经过点A，与BD交于点P，与BC交于点Q.AP的长度为（）

A、 $\sqrt{2}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $\sqrt{3}$

查看试题解析
10. 如图，在平面直角坐标系中，正方形纸片ABCD的顶点A的坐标为 $(- 1 ， 3)$ ，在纸片中心挖去边长为 $\sqrt{2}$ 的正方形 $A_{1} B_{1} C_{1} D_{1}$ ，将该纸片以О为旋转中心进行逆时针旋转，每次旋转45°，则第258次旋转后，点C和点 $B_{1}$ 的坐标分别为（）

A、 $(- 3 ， - 1)$ ， $(1 ， 0)$ B、 $(- 3 ， - 1)$ ， $(0 ， - 1)$ C、 $(3 ， 1)$ ， $(1 ， 0)$ D、 $(3 ， 1)$ ， $(0 ， - 1)$

查看试题解析

二、填空题

11. 计算： $\sqrt{16} - {(- \frac{1}{3})}^{- 1} =$ .

查看试题解析
12. 不等式组 ${\begin{array}{l} x + 1 \geq 0 \\ 2 x - 6 < - x \end{array} ，$ 的解集为.

查看试题解析
13. 四张材质与大小完全相同的卡片上分别写有“张飞”、“李逡”、“长矛”、“板斧”4个词条，将四张卡片放置于暗箱内摇匀后随机抽取两张，则抽到的人物与所便兵器恰巧对应的概率是.

查看试题解析
14. 已知正方形ABCD的边长为12，点E、F分别在AD、CD上， $A E = D F = 4$ ，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为.

查看试题解析
15. 在 $R t △ A C B$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $B C = 2 \sqrt{3}$ ，以 $C$ 为圆心，AC长为半径画弧，交AB于点D，交BC于点E，以E为圆心，CE长为半径画弧，交AB于点F.交弧AE于点G，则图中阴影部分的面积为.

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{2 x - 1}{x + 1} - 1) \div \frac{x - 2}{x^{2} + 2 x + 1}$ ，其中 $x$ 为－1，1，2中一个合适的值.

查看试题解析
17. 某社团为了调查大众对河南名吃的喜爱程度，设计了四个选项：A.芝麻翅中翅；B烩面；C.胡辣汤；D.开花馍.社团在步行街随机抽取部分路人进行调查，要求受访者只能勾选一个最喜欢的名吃，组织者依据勾选情况绘制如下两幅不完整统计图.

请根据统计图提供的信息，解答下列问题：

(1)、此次共抽取了名路人；

(2)、请通过计算补全条形统计图；

(3)、若此时步行街共有2700名路人，请估计喜欢A名吃的人数.

查看试题解析

18. 无影塔，国家级保护文物，位于河南汝南城南，俗传冬至正午无塔影，故称无影塔.相传为唐代和尚悟颖所建，故又称“悟颖塔”.如图，九（1）班数学活动小组要测量古塔的高度，他们借助测角仪和皮尺进行了实地测量﹑请根据给出的测量数据计算古塔的高度AB.

（结果精确到0.1米，参考数据： $\sin 67 ° \approx 0.92$ ， $\cos 67 ° \approx 0.39$ ， $\tan 67 ° \approx 2.36$ ， $\sin 22 ° \approx 0.37$ ， $\cos 22 ° \approx 0.93$ ， $\tan 22 ° \approx 0.40$ ）

项目	内容
课题	测量无影塔的高度
测量示意图		说明：CD的长为3.2米
测量数据	从C测A的仰角	从C测B的俯角	BD的长度
测量数据	67°	22°	8米

查看试题解析

19. 2021年，我们将迎来中国共产党建党100周年.某学校计划购进党徽和团徽共60件（1件＝100枚）.已知购买3件党徽和5件团徽需要1290元，购买5件党徽和10件团徽需要2400元

(1)、求党徽和团徽的单价（单位：元/件）；

(2)、若要使该学校的购买所需费用在9180元的限额内，最多可购进党徽多少件？

查看试题解析
20. 如图，已知抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点B和点C，与y轴交于点 $A (0 ， - 3)$ ，且 $O A = 3 O C$ .点 $P$ 是对称轴左侧的抛物线上一点，过点 $P$ 作 $P Q / / x$ 轴，交抛物线于点Q.

(1)、若 $P Q = 5$ ，求抛物线的解析式以及点Q的坐标；

(2)、若点 $P$ 沿抛物线问上移动，使得对应的 $9 \leq P Q \leq 10$ ，求移动过程中点 $P$ 的纵坐标， $y_{P}$ 的取值范围.

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ C A B$ 的平分线AD交BC于点E，交 $△ A B C$ 的外接圆 $⊙ O$ 于点D.过点D作 $⊙ O$ 的切线DF，连接BD.

(1)、求证： $∠ A D F = ∠ A B D$ .

(2)、若 $A C = 4$ ， $A B = 5$ .
①当 $∠ A C B = ∠ A D F$ 时，求线段 $B D$ 的长为.

②当四边形OCDB为平行四边形时， $⊙ O$ 的半径等于.

查看试题解析

22. 某班“数学兴趣小组”在学习“勾股定理”章节的内容后，遇到这样的问题：如图，在直角三角形ACB中，

C A = 6

，

C B = 8

，点D是边CB上的一个动点（不与B、C重合），连接AD.若

△ A D B

是等腰三角形，求线段CD的长.

方法一：小敏利用刚学习的勾股定理进行解决，当 $△ A B D$ 为等腰三角形时， $A D = B D$ ，设 $C D = x$ ，则 $B D = 8 - x$ ，所以 $A D = B D = 8 - x$ ，在直角三角形ACD中，利用勾股定理可得， $6^{2} + x^{2} = {(8 - x)}^{2}$ ，

解得 $x = \frac{7}{4}$ .故当 $△ A B D$ 为等腰三角形时，CD的长为 $\frac{7}{4}$ .

方法二：小聪提前预习了函数这一章节的内容，他尝试利用函数的方法探究并解决该问题.

下面是他的探究讨程，请你补充完整.

(1)、根据点D在PC上的不同付置，画出相应图形，测量出线段CD、AD的长度，得出下面的表格：

CD	0	1	2	3	4	5	6	7	8
AD	6	6.1	6.3	6.7	7.2	7.8	8.5	9.2	a

①表格中 $a$ 的值为.

②小聪分析得知不用测量BD的值，因为CD与BD满足关系式：.

(2)、将CD的长作为自变量x，AD的长为x的函数，记为y，在下面平面直角坐标系中画出函数y关于x的图象，并写出该函数的一条性质： ▲ .

(3)、继续在平面直角坐标系画出小聪所需的其他函数图象，并结合图形直接写出，当

△ A B D

为等腰三角形时，线段CD的长度的近似值（精确到0.1）.

查看试题解析

23. 如图1，在等腰 $R t △ A B C$ 中， $A B = A C$ ，点D为斜边AB边上一动点（不含端点）.作 $∠ E D F = 90 °$ ，DE，DF分别交AB，AC于点E和点F.请根据图形解答下面问题：

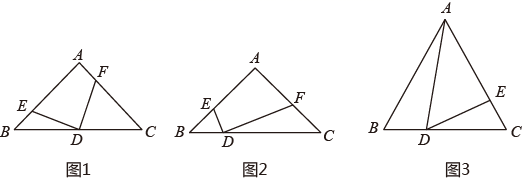(1)、（问题发现）
如图1，若点D为BC边中点.请直接写出DE，DF的数量关系.

(2)、（类比探究）
如图2，若点D为BC边上一动点，且 $D C = m B D$ .猜想DF与DE的数量关系.并证明你的结论.

(3)、（拓展应用）
如图3，在边长为4的等边 $△ A B C$ 中，点D为BC边上一动点，作 $∠ A D E = 60 °$ .DE交AC边于点E.请问在点D的运动过程中，CE是否有最大值.如果有，求出最大值；如果没有，请说明理由.

查看试题解析