河南省三门峡市2021年数学中考二模试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. 下列四个数中最小的数是( )A、-1 B、-3 C、0 D、2. 据三门峡市统计局数据,2020年三门峡市全年GDP约为1451亿元,数据“1451亿”用科学记数法可表示为( )A、 B、 C、 D、3. 在下列运算中,正确的是( )A、 B、 C、 D、4. 某个几何体的三视图如图所示,该几何体是( )
 A、
A、 B、
B、 C、
C、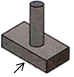 D、
D、 5. 如图,直线AB∥CD,则下列结论正确的是( )
5. 如图,直线AB∥CD,则下列结论正确的是( )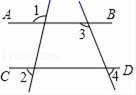 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°6. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°6. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( ) A、8 B、11 C、16 D、177. 一元二次方程 根的情况是( )
A、8 B、11 C、16 D、177. 一元二次方程 根的情况是( )
A、无实数根 B、有一个正根,一个负根 C、有两个正根,且都小于3 D、有两个正根,且有一根大于38. 七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率为( ) A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )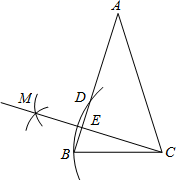 A、2 B、3 C、 D、10. 如图,在单位为1的方格纸上, , , ,…,是斜边在 轴上,斜边长分别为2,4,6,…,的等腰直角三角形,若 的顶点坐标分别为 , , ,则依图中所示规律, 的坐标为( )
A、2 B、3 C、 D、10. 如图,在单位为1的方格纸上, , , ,…,是斜边在 轴上,斜边长分别为2,4,6,…,的等腰直角三角形,若 的顶点坐标分别为 , , ,则依图中所示规律, 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算 的值是.12. 如图,Rt 中, ,顶点 , 分别在反比例函数 与 的图象上,则 的值为.
 13. 不等式组 的最小整数解是 .14. 如图,矩形ABCD中,AB= ,BC=1,将矩形ABCD绕点A旋转得到矩形AB′C′D′,点C的运动路径为弧CC′,当点B′落在CD上时,则图中阴影部分的面积为
13. 不等式组 的最小整数解是 .14. 如图,矩形ABCD中,AB= ,BC=1,将矩形ABCD绕点A旋转得到矩形AB′C′D′,点C的运动路径为弧CC′,当点B′落在CD上时,则图中阴影部分的面积为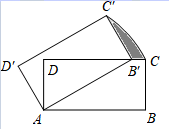 15. 如图,在平行四边形 中, , ,点 为直线 上的一个动点,四边形 为平行四边形, 为 的中点,则 的最小值为.
15. 如图,在平行四边形 中, , ,点 为直线 上的一个动点,四边形 为平行四边形, 为 的中点,则 的最小值为.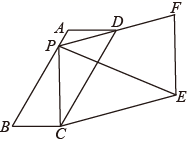
三、解答题
-
16. 下面是小锐同学进行分式化简的过程,请认真阅读并完成相应任务.
…第一步
…第二步
…第三步
…第四步
…第五步
…第六步
(1)、填空:①以上化简步骤中,第步是进行分式的通分,通分的依据是;
②第步开始出现错误,这一步错误的原因是.
(2)、请从出现错误的步骤开始继续进行该分式的化简;(3)、除纠正上述错误外,请你根据平时的学习经验,就分式化简时还需注意的事项给其他同学提一条建议.17. 为了响应全民阅读的号召,某社区开展了为期一年的“读书伴我行”阅读活动,在阅读活动开展之初,随机抽取若干名社区居民,对其年阅读量(单位:本)进行了调查统计与分析,结果如下:平均数
中位数
众数
最大值
最小值
方差
6.9
7.5
8
16
1
18.69
经过一年的“读书伴我行”阅读活动,某社区再次对这部分居民的年阅读量进行调查,并对收集的数据进行了整理、描述和分析,下面给出了部分信息.
a.居民的年阅读量统计表如下:
阅读量
2
4
5
8
9
10
11
12
13
16
21
人数
5
5
5
3
2
m
5
5
3
7
n
b.分组整理后的居民阅读量统计表、统计图如下:
组别
阅读量/本
频数
15
13

c.居民阅读量的平均数、中位数、众数、最大值、最小值、方差如下:
平均数
中位数
众数
最大值
最小值
方差
10.4
10.5
q
21
2
30.83
根据以上信息,回答下列问题:
(1)、样本容量为;(2)、 ; ; ;(3)、根据社区开展“读书伴我行”阅读活动前、后随机抽取的部分居民阅读量的两组调查结果,请至少从两个方面对社区开展阅读活动的效果进行评价.18. 宝轮寺塔——中国四大回音建筑之一,位于三门峡市陕州风景区,始建于隋唐时期,因能发出“呱呱”的声音而俗称“蛤蟆塔”.当地某校数学实践活动小组的同学们一起对该塔的高度( )进行测量.因塔底部 无法直接到达,制定了如下的测量方案:先在该塔正前方广场地面 处测得塔尖 的仰角( )为45°,因广场面积有限,无法再向 点的正后方移动,故操控无人机飞到 点正上方10米的 处测得塔尖 的仰角为32°, , , , 四点在同一个平面内,求塔高( )为多少米.(结果精确到0.1米,参考数据: , , ) 19. 为加强公民的节水意识,合理利用水资源,某市对居民用水实行阶梯水价.居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于 .如图,折线表示实行阶梯水价后每月水费 (元)与用水量 ( )之间的函数关系.其中线段 表示第二级阶梯时 与 之间的函数关系.
19. 为加强公民的节水意识,合理利用水资源,某市对居民用水实行阶梯水价.居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于 .如图,折线表示实行阶梯水价后每月水费 (元)与用水量 ( )之间的函数关系.其中线段 表示第二级阶梯时 与 之间的函数关系. (1)、写出点 的实际意义;(2)、求线段 所在直线的表达式;(3)、某户5月份缴水费108元,求相应用水量为多少立方米?20. 小锐同学是一个数学学习爱好者,他在一本数学课外读物上看到一个课本上没有的与圆相关的角---弦切角(弦切角的定义:把顶点在圆上,一边与圆相切,另一边和圆相交的角叫做弦切角),并尝试用所学的知识研究弦切角的有关性质.
(1)、写出点 的实际意义;(2)、求线段 所在直线的表达式;(3)、某户5月份缴水费108元,求相应用水量为多少立方米?20. 小锐同学是一个数学学习爱好者,他在一本数学课外读物上看到一个课本上没有的与圆相关的角---弦切角(弦切角的定义:把顶点在圆上,一边与圆相切,另一边和圆相交的角叫做弦切角),并尝试用所学的知识研究弦切角的有关性质. (1)、如图,直线 与⊙O相切于 点, , 为⊙O上不同于 的两点,连接 , , .请你写出图中的两个弦切角;(不添加新的字母和线段)(2)、小锐目测 和 可能相等,并通过测量的方法验证了他的结论,你能帮小锐用几何推理的方法证明结论的正确性吗?
(1)、如图,直线 与⊙O相切于 点, , 为⊙O上不同于 的两点,连接 , , .请你写出图中的两个弦切角;(不添加新的字母和线段)(2)、小锐目测 和 可能相等,并通过测量的方法验证了他的结论,你能帮小锐用几何推理的方法证明结论的正确性吗?已知:如图,直线 与⊙O相切于 点, , 为圆上不同于 的两点,连接 , , .
求证: .
(3)、如果我们把上述结论称为弦切角定理,请你用一句话概括弦切角定理.21. 已知抛物线 : 和点 , .(1)、直接写出抛物线 的顶点坐标(用含 的式子表示);(2)、试分析抛物线 与线段 有公共点的个数情况,并写出相应的 的取值范围.22. 如图,点 是以 为直径的半圆上一点,连接 ,点 是 上一个动点,连接 ,作 交 于点 ,交半圆于点 .已知: ,设 的长度为 , 的长度为 , 的长度为 (当点 与点 重合时, , ,当点 与点 重合时, , ).小锐同学根据学习函数的经验,分别对函数 , 随自变量 变化而变化的规律进行了探究.

下面是小锐同学的探究过程,请补充完整:
(1)、按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值,请补全表格:cm
0
1
2
3
4
5
6
7
8
cm
8.00
5.81
4.38
3.35
2.55
1.85
1.21
0.60
0.00
cm
0.00
0.90
2.24
2.67
2.89
2.83
2.34
0.00
上表中 .(精确到0.1)
(2)、在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点 , ,并画出函数 , 的图象( 已经画出); (3)、结合函数图象解决问题:
(3)、结合函数图象解决问题:①当 , 的长都大于 时, 长度的取值范围约是 ▲ ;(精确到0.1)
②继续在同一坐标系中画出所需的函数图象,判断点 , , 能否在以 为圆心的同一个圆上?(填“能”或“否”)
23. 如图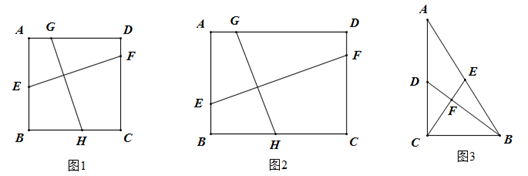 (1)、问题发现:
(1)、问题发现:如图1,在正方形 中,点 , , , 分别在边 , , , 上,且 ,则 ;
(2)、类比探究:如图2,在(1)的条件下,把“正方形 ”改为“矩形 ,且 , ”其它条件不变,则 ▲ ,证明你的结论;
(3)、拓展应用:如图3,在Rt 中, , , ,点 为 的中点,连接 ,点 为 上一点, ,则 .