河南省濮阳市2021年数学中考二模试卷
试卷更新日期:2021-09-28 类型:中考模拟
一、单选题
-
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 下列几何体中,主视图为三角形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 新型冠状病毒是目前已知的第7种可以感染人的冠状病毒,其直径约为125纳米,已知长度单位1纳米 米.用科学记数法表示125纳米是( )A、 米 B、 米 C、 米 D、 米4. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
3. 新型冠状病毒是目前已知的第7种可以感染人的冠状病毒,其直径约为125纳米,已知长度单位1纳米 米.用科学记数法表示125纳米是( )A、 米 B、 米 C、 米 D、 米4. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )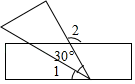 A、48° B、78° C、92° D、102°5. 下面计算正确的是( )A、 B、 C、 D、6. 关于 的方程 的根的情况,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 如图是某公司去年8~12月份生产成本统计图,设9~11月每个月生产成本的下降率都为 ,根据图中信息,得到 所满足的方程是( )
A、48° B、78° C、92° D、102°5. 下面计算正确的是( )A、 B、 C、 D、6. 关于 的方程 的根的情况,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 如图是某公司去年8~12月份生产成本统计图,设9~11月每个月生产成本的下降率都为 ,根据图中信息,得到 所满足的方程是( ) A、 B、 C、 D、8. 已知点 , , 都在二次函数 的图象上,则( )A、 B、 C、 D、9. 如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC、AO于点M、N,再分别以M、N为圆心,大于 MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
A、 B、 C、 D、8. 已知点 , , 都在二次函数 的图象上,则( )A、 B、 C、 D、9. 如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC、AO于点M、N,再分别以M、N为圆心,大于 MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( ) A、 B、 C、 D、10. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 ,则 (n为正整数)的坐标是( )
A、 B、 C、 D、10. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 ,则 (n为正整数)的坐标是( )
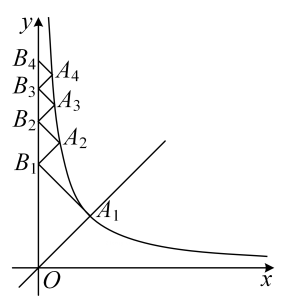 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:(π-3) +(- ) =12. 不等式组 的所有整数解的和是.13. 五一假期,甲.乙丙、丁四名同学参加社区防疫志愿者活动,若四名同学被随机分成两组,每组两人,则甲和乙恰好在同一组的概率为.14. 如图,在 中,已知 , ,垂足为D. .若E是AD的中点,则 .
 15. 如图,在矩形 中, , ,延长AD至点F,使得 ,以点A为圆心,AD的长为半径画弧,交AB于点E,P为上一动点,连接FP并延长交AB于点G,当BG的长度最短时,阴影部分的周长为.
15. 如图,在矩形 中, , ,延长AD至点F,使得 ,以点A为圆心,AD的长为半径画弧,交AB于点E,P为上一动点,连接FP并延长交AB于点G,当BG的长度最短时,阴影部分的周长为.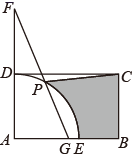
三、解答题
-
16. 先化简,再求值: ,其中 .17. 以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了m名新聘毕业生的专业情况,并将调查结果绘制成如下两幅不完整的统计图:


根据以上信息,解答下列问题:
(1)、m= , n=;(2)、请补全条形统计图;(3)、在扇形统计图中,“软件”所对应圆心角的度数是;(4)、若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有名.18. 教育部颁布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 , 米, 米(测角器的高度忽略不计,结果精确到0.1米,参考数据: , , , , )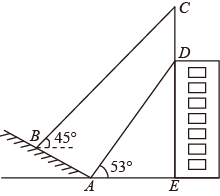 (1)、求点B距水平地面AE的高度;(2)、若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.19. 为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲、乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
(1)、求点B距水平地面AE的高度;(2)、若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.19. 为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲、乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:时间
销售数量(个)
销售收入(元)(销售收入=售价×销售数量)
甲种型号
乙种型号
第一月
22
8
1100
第二月
38
24
2460
(1)、求甲、乙两种型号水杯的售价;(2)、第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下,请问当甲种型号水杯购进多少个时,第三个月的利润最大,最大利润是多少?20. 如图,在 中, , ,以BC边上一点О为圆心,OC的长为半径做 , 恰好与边AB相切于点D.并与BC边交于点E,点F在BC右侧的 上,连接DF,CF. (1)、求证;点D为边AB的中点(2)、若 的半径长为1,填空:
(1)、求证;点D为边AB的中点(2)、若 的半径长为1,填空:①连接AF,当 时,四边形ACFD是菱形;
②连接DC,DE,EF,当 时,四边形DCFE是矩形
21. 如图,抛物线 与 交于A,B两点,与y轴交于点C,且 ,点D是抛物线的顶点, (1)、求抛物线 的解析式及顶点D的坐标.(2)、平移抛物线 后,得到抛物线: .若点 是抛物线 上任意一点,且当 时,y的最小值是-2,试求出m的值22. 如图1,△ABC是等腰直角三角形,∠A=90°,BC=4cm,点P在△ABC的边上沿路径B→A→C移动,过点P作PD⊥BC于点D,设BD=xcm,△BDP的面积为ycm2(当点P与点B或点C重合时,y的值为0).
(1)、求抛物线 的解析式及顶点D的坐标.(2)、平移抛物线 后,得到抛物线: .若点 是抛物线 上任意一点,且当 时,y的最小值是-2,试求出m的值22. 如图1,△ABC是等腰直角三角形,∠A=90°,BC=4cm,点P在△ABC的边上沿路径B→A→C移动,过点P作PD⊥BC于点D,设BD=xcm,△BDP的面积为ycm2(当点P与点B或点C重合时,y的值为0).
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)、自变量x的取值范围是;(2)、通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm
0
1
2
3
4
y/cm2
0
m
2
n
0
请直接写出m= , n=;
(3)、如图2,在平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(4)、结合画出的函数图象,解决问题:当△BDP的面积为1cm2时,BD的长度约为cm.(数值保留一位小数)23. 如图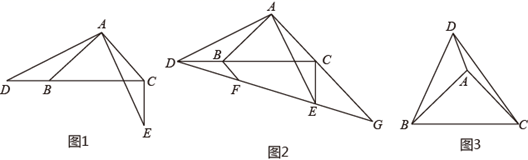 (1)、(问题背景)如图1,在 中, , ,D是直线BC上的一点,将线段AD绕点A逆时针旋转90°至AE,连接CE,求证: ;(2)、(尝试应用)如图2,在(1)的条件下,延长DE,AC交于点G, 交DE于点F.求证: ;(3)、(拓展创新)如图3, 是 内一点, , , ,直接写出 的面积为.
(1)、(问题背景)如图1,在 中, , ,D是直线BC上的一点,将线段AD绕点A逆时针旋转90°至AE,连接CE,求证: ;(2)、(尝试应用)如图2,在(1)的条件下,延长DE,AC交于点G, 交DE于点F.求证: ;(3)、(拓展创新)如图3, 是 内一点, , , ,直接写出 的面积为.