江苏中考数学历年真题分类卷5 一次方程和一次不等式
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 《孙子算经》中有一道题,原文是“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳长y尺,可列方程组为( )A、 B、 C、 D、2. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、3. 方程组 的解是( )A、 B、 C、 D、4. 《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的 ,则甲有50钱,乙若得到甲所有钱的 ,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )A、 B、 C、 D、5. 某公司上半年生产甲,乙两种型号的无人机若干架.已知甲种型号无人机架数比总架数的一半多11架,乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机 架,乙种型号无人机 架.根据题意可列出的方程组是( )A、 B、 C、 D、6. 若a>b,则下列等式一定成立的是( )A、a>b+2 B、a+1>b+1 C、﹣a>﹣b D、|a|>|b|7. 把 这 个数填入 方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图 ),是世界上最早的“幻方”.图 是仅可以看到部分数值的“九宫格”,则其中 的值为( )
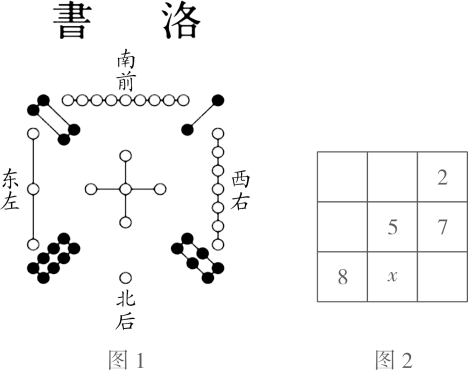 A、1 B、3 C、4 D、68. 若 , ,则 的值等于( )A、5 B、1 C、-1 D、-59. 不等式 的解集在数轴上表示正确的是( )A、
A、1 B、3 C、4 D、68. 若 , ,则 的值等于( )A、5 B、1 C、-1 D、-59. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、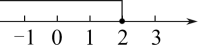 D、
D、 10. 不等式组 的解集在数轴上表示为( ).A、
10. 不等式组 的解集在数轴上表示为( ).A、 B、
B、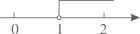 C、
C、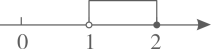 D、
D、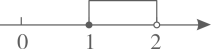 11. 如果 ,那么下列不等式正确的是( )A、 B、 C、 D、12. 已知a、b满足方程组 ,则a+b的值为( )A、2 B、4 C、—2 D、—413. 下列各数轴上表示的 的取值范围可以是不等式组 的解集的是( )A、
11. 如果 ,那么下列不等式正确的是( )A、 B、 C、 D、12. 已知a、b满足方程组 ,则a+b的值为( )A、2 B、4 C、—2 D、—413. 下列各数轴上表示的 的取值范围可以是不等式组 的解集的是( )A、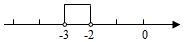 B、
B、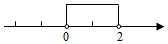 C、
C、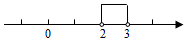 D、
D、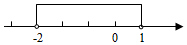 14. 不等式 的非负整数解有( )A、1个 B、2个 C、3个 D、4个15. 实数a、b、c满足a>b且ac<bc,它们在数轴上的对应点的位置可以是( )A、
14. 不等式 的非负整数解有( )A、1个 B、2个 C、3个 D、4个15. 实数a、b、c满足a>b且ac<bc,它们在数轴上的对应点的位置可以是( )A、 B、
B、 C、
C、 D、
D、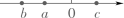 16. 某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为( )A、10 B、9 C、8 D、7
16. 某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为( )A、10 B、9 C、8 D、7二、填空题
-
17. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马天追上慢马.18. 不等式组 的解集是.19. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子最井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是尺.20. 已知x、y满足方程组 ,则 的值为.21. 不等式组 的解集为 .22. 若 ,是关于 、 的二元一次方程 的解,则 .23. 《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?”设共有 个人共同出钱买鸡,根据题意,可列一元一次方程为.24. 不等式组 的解集是.25. 下面3个天平左盘中“△”“□”分别表示两种质量不同的物体,则第三个天平右盘中砝码的质量为.

三、计算题
-
26. 解方程组和不等式组:(1)、(2)、27. 解不等式组:28.(1)、计算: ﹣(π﹣1)0﹣sin30°;(2)、解不等式组: .29. 解方程组: .30.(1)、计算:(2)、解不等式组:31. 解不等式组: .32. 解不等式组 ,并写出它的最大负整数解.33. 解方程组 .34. 解不等式组:35. 解不等式组: .36. 解不等式组 ,并写出它的所有负整数解
四、解答题
-
37. 甲、乙两工程队共同修建150km的公路,原计划30个月完工.实际施工时,甲队通过技术创新,施工效率提高了50%,乙队施工效率不变,结果提前5个月完工.甲、乙两工程队原计划平均每月分别修建多长?38. 《九章算术》被历代数学家尊为“算经之首”.下面是其卷中记载的关于“盈不足”的一个问题:今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?这段话的意思是:今有人合伙买金,每人出400钱,会剩余3400钱;每人出300钱,会剩余100钱.合伙人数、金价各是多少?请解决上述问题.39. 解不等式组 ,并写出满足不等式组的所有整数解.40. 解不等式 ,并在数轴上表示解集.41. 已知方程组 的解也是关于x、y的方程 的一个解,求a的值.42. 本地某快递公司规定:寄件不超过 千克的部分按起步价计费;寄件超过 千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准
目的地
起步价(元)
超过 千克的部分
(元 千克)
上海
北京
实际收费
目的地
质量
费用(元)
上海
2
9
北京
3
22
求 , 的值.
43. 某停车场的收费标准如下:中型汽车的停车费为15元/辆,小型汽车的停车费为8元/辆.现在停车场内停有30辆中、小型汽车,这些车共缴纳停车费324元,求中、小型汽车各有多少辆?44. 某公司用火车和汽车运输两批物资,具体运输情况如下表所示:所用火车车皮数量(节)
所用汽车数量(辆)
运输物资总量(吨)
第一批
2
5
130
第二批
4
3
218
试问每节火车车皮和每辆汽车平均各装物资多少吨?
45. 解不等式组 并把解集在数轴上表示出来.46. 解不等式 -x>1,并把它的解集在数轴上表示出来.五、综合题
-
47. 为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.(1)、这两种消毒液的单价各是多少元?(2)、学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不少于A型消毒液数量的 ,请设计出最省钱的购买方案,并求出最少费用.48. 阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数x、y满足 ①, ②,求 和 的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由① ②可得 ,由① ② 可得 .这样的解题思想就是通常所说的“整体思想”.
解决问题:
(1)、已知二元一次方程组 ,则 , ;(2)、某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?(3)、对于实数x、y,定义新运算: ,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知 , ,那么 .49. 如图,“开心”农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .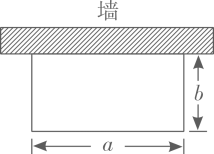 (1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.50. 解不等式 .
(1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.50. 解不等式 .解:去分母,得 .
……
(1)、请完成上述解不等式的余下步骤:(2)、解题回顾:本题“去分母”这一步的变形依据是 (填“A”或“B”)A、不等式两边都乘(或除以)同一个正数,不等号的方向不变; B、不等式两边都乘(或除以)同一个负数,不等号的方向改变.