江苏中考数学历年真题分类卷7 函数综合题和压轴题
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 如图,四边形 中, ,垂足分别为E,F,且 , .动点P,Q均以 的速度同时从点A出发,其中点P沿折线 运动到点B停止,点Q沿 运动到点B停止,设运动时间为 , 的面积为 ,则y与t对应关系的图象大致是( )
 A、
A、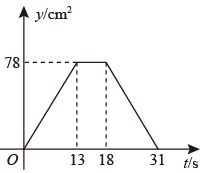 B、
B、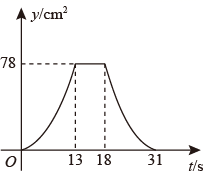 C、
C、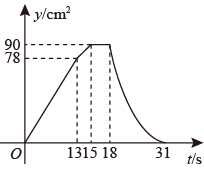 D、
D、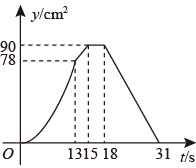 2. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )
2. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )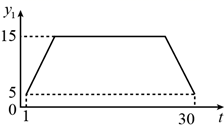 A、
A、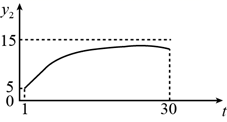 B、
B、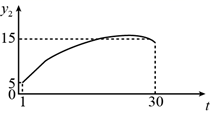 C、
C、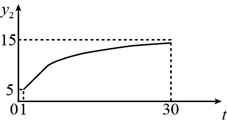 D、
D、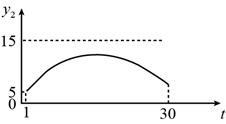 3. 设 , 分别是函数 , 图象上的点,当 时,总有 恒成立,则称函数 , 在 上是“逼近函数”, 为“逼近区间”.则下列结论:
3. 设 , 分别是函数 , 图象上的点,当 时,总有 恒成立,则称函数 , 在 上是“逼近函数”, 为“逼近区间”.则下列结论:①函数 , 在 上是“逼近函数”;②函数 , 在 上是“逼近函数”;③ 是函数 , 的“逼近区间”;④ 是函数 , 的“逼近区间”.其中,正确的有( )
A、②③ B、①④ C、①③ D、②④4. 在 中, , , ,点P是 所在平面内一点,则 取得最小值时,下列结论正确的是( )A、点P是 三边垂直平分线的交点 B、点P是 三条内角平分线的交点 C、点P是 三条高的交点 D、点P是 三条中线的交点5. 如图,线段 ,点 、 在 上, .已知点 从点 出发,以每秒1个单位长度的速度沿着 向点 移动,到达点 后停止移动,在点 移动过程中作如下操作:先以点 为圆心, 、 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 的移动时间为(秒).两个圆锥的底面面积之和为 .则 关于 的函数图象大致是( )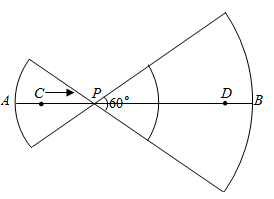 A、
A、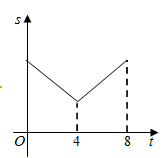 B、
B、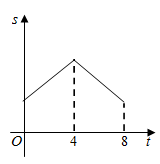 C、
C、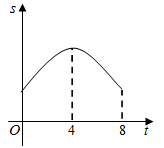 D、
D、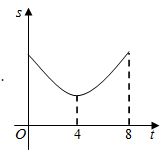 6. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
6. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )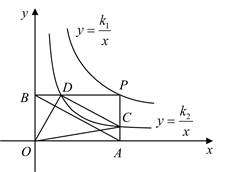 A、①② B、①③ C、②③ D、①7. 如图①,E为矩形ABCD的边AD上一点,点P从点B出发沿折线B﹣E﹣D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是1cm/s.现P,Q两点同时出发,设运动时间为x(s),△BPQ的面积为y(cm2),若y与x的对应关系如图②所示,则矩形ABCD的面积是( )
A、①② B、①③ C、②③ D、①7. 如图①,E为矩形ABCD的边AD上一点,点P从点B出发沿折线B﹣E﹣D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是1cm/s.现P,Q两点同时出发,设运动时间为x(s),△BPQ的面积为y(cm2),若y与x的对应关系如图②所示,则矩形ABCD的面积是( )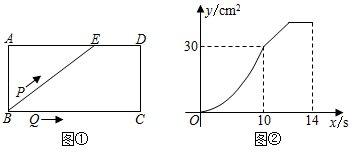 A、96cm2 B、84cm2 C、72cm2 D、56cm28. 如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到 , 与BC,AC分别交于点D,E.设 , 的面积为 ,则 与 的函数图象大致为( )
A、96cm2 B、84cm2 C、72cm2 D、56cm28. 如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到 , 与BC,AC分别交于点D,E.设 , 的面积为 ,则 与 的函数图象大致为( )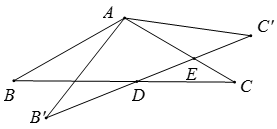 A、
A、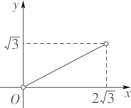 B、
B、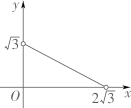 C、
C、 D、
D、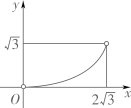 9. 随着时代的进步,人们对 (空气中直径小于等于 微米的颗粒)的关注日益密切.某市一天中 的值 ( )随时间 ( )的变化如图所示,设 表示 时到 时 的值的极差(即 时到 时 的最大值与最小值的差),则 与 的函数关系大致是( )
9. 随着时代的进步,人们对 (空气中直径小于等于 微米的颗粒)的关注日益密切.某市一天中 的值 ( )随时间 ( )的变化如图所示,设 表示 时到 时 的值的极差(即 时到 时 的最大值与最小值的差),则 与 的函数关系大致是( )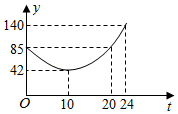 A、
A、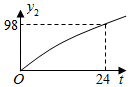 B、
B、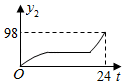 C、
C、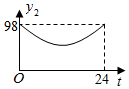 D、
D、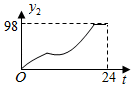
二、综合题
-
10. 如图,在平面直角坐标系 中,正比例函数 和二次函数 的图象都经过点 和点B,过点A作 的垂线交x轴于点C.D是线段 上一点(点D与点A、O、B不重合),E是射线 上一点,且 ,连接 ,过点D作x轴的垂线交抛物线于点F,以 、 为邻边作 .
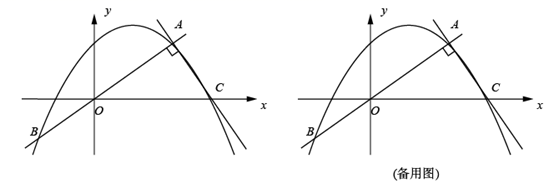 (1)、填空: , ;(2)、设点D的横坐标是 ,连接 .若 ,求t的值;(3)、过点F作 的垂线交线段 于点P.若 ,求 的长.11. 为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:
(1)、填空: , ;(2)、设点D的横坐标是 ,连接 .若 ,求t的值;(3)、过点F作 的垂线交线段 于点P.若 ,求 的长.11. 为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:该地区每周接种疫苗人数统计表
周次
第1周
第2周
第3周
第4周
第5周
第6周
第7周
第8周
接种人数(万人)
7
10
12
18
25
29
37
42
该地区全民接种疫苗情况扇形统计图
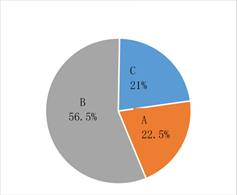
A:建议接种疫苗已接种人群
B:建议接种疫苗尚未接种人群
C:暂不建议接种疫苗人群
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3周开始这些点大致分布在一条直线附近,现过其中两点 、 作一条直线(如图所示,该直线的函数表达式为 ),那么这条直线可近似反映该地区接种人数的变化趋势.
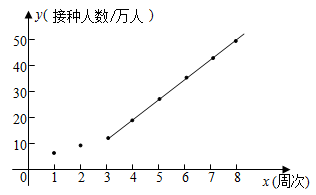
请根据以上信息,解答下列问题:
(1)、这八周中每周接种人数的平均数为万人:该地区的总人口约为万人;(2)、若从第9周开始,每周的接种人数仍符合上述变化趋势.①估计第9周的接种人数约为 ▲ 万人;
②专家表示:疫苗接种率至少达60%,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
(3)、实际上,受疫苗供应等客观因素,从第9周开始接种人数将会逐周减少 万人,为了尽快提高接种率,一旦周接种人数低于20万人时,卫生防疫部门将会采取措施,使得之后每周的接种能力一直维持在20万人.如果 ,那么该地区的建议接种人群最早将于第几周全部完成接种?12. 在平面直角坐标系中,O为坐标原点,直线 与x轴交于点B,与y轴交于点C,二次函数 的图象过B、C两点,且与x轴交于另一点A,点M为线段 上的一个动点,过点M作直线l平行于y轴交 于点F,交二次函数 的图象于点E.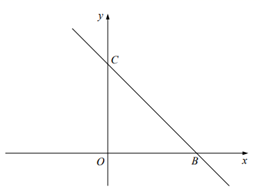 (1)、求二次函数的表达式;(2)、当以C、E、F为顶点的三角形与 相似时,求线段 的长度;(3)、已知点N是y轴上的点,若点N、F关于直线 对称,求点N的坐标.13. 将一张三角形纸片ABC放置在如图所示的平面直角坐标系中,点A(﹣6,0),点B(0,2),点C(﹣4,8),二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,该抛物线的对称轴经过点C,顶点为D.
(1)、求二次函数的表达式;(2)、当以C、E、F为顶点的三角形与 相似时,求线段 的长度;(3)、已知点N是y轴上的点,若点N、F关于直线 对称,求点N的坐标.13. 将一张三角形纸片ABC放置在如图所示的平面直角坐标系中,点A(﹣6,0),点B(0,2),点C(﹣4,8),二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,该抛物线的对称轴经过点C,顶点为D.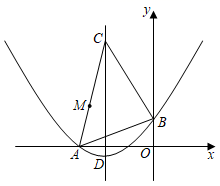 (1)、求该二次函数的表达式及点D的坐标;(2)、点M在边AC上(异于点A,C),将三角形纸片ABC折叠,使得点A落在直线AB上,且点M落在边BC上,点M的对应点记为点N,折痕所在直线l交抛物线的对称轴于点P,然后将纸片展开.
(1)、求该二次函数的表达式及点D的坐标;(2)、点M在边AC上(异于点A,C),将三角形纸片ABC折叠,使得点A落在直线AB上,且点M落在边BC上,点M的对应点记为点N,折痕所在直线l交抛物线的对称轴于点P,然后将纸片展开.①请作出图中点M的对应点N和折痕所在直线l;(要求:尺规作图,不写作法,保留作图痕迹)
②连接MP,NP,在下列选项中:A.折痕与AB垂直,B.折痕与MN的交点可以落在抛物线的对称轴上,C. = ,D. = ,所有正确选项的序号是 .
③点Q在二次函数y=ax2+bx+c(a≠0)的图象上,当 PDQ∼ PMN时,求点Q的坐标.
14. 如图,在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于点A(﹣3,0)和点B(5,0),顶点为点D,动点M、Q在x轴上(点M在点Q的左侧),在x轴下方作矩形MNPQ,其中MQ=3,MN=2.矩形MNPQ沿x轴以每秒1个单位长度的速度向右匀速运动,运动开始时,点M的坐标为(﹣6,0),当点M与点B重合时停止运动,设运动的时间为t秒(t>0).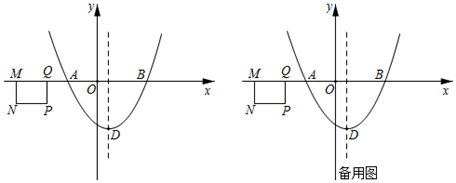 (1)、b= , c=.(2)、连接BD,求直线BD的函数表达式.(3)、在矩形MNPQ运动的过程中,MN所在直线与该二次函数的图象交于点G,PQ所在直线与直线BD交于点H,是否存在某一时刻,使得以G、M、H、Q为顶点的四边形是面积小于10的平行四边形?若存在,求出t的值;若不存在,请说明理由.(4)、连接PD,过点P作PD的垂线交y轴于点R,直接写出在矩形MNPQ整个运动过程中点R运动的路径长.15. 如图,抛物线 与x轴交于A(-1,0),B(4,0),与y轴交于点C.连接AC,BC,点P在抛物线上运动.
(1)、b= , c=.(2)、连接BD,求直线BD的函数表达式.(3)、在矩形MNPQ运动的过程中,MN所在直线与该二次函数的图象交于点G,PQ所在直线与直线BD交于点H,是否存在某一时刻,使得以G、M、H、Q为顶点的四边形是面积小于10的平行四边形?若存在,求出t的值;若不存在,请说明理由.(4)、连接PD,过点P作PD的垂线交y轴于点R,直接写出在矩形MNPQ整个运动过程中点R运动的路径长.15. 如图,抛物线 与x轴交于A(-1,0),B(4,0),与y轴交于点C.连接AC,BC,点P在抛物线上运动.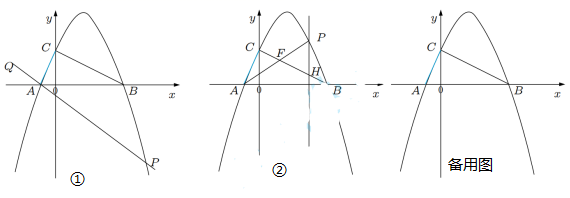 (1)、求抛物线的表达式;(2)、如图①,若点P在第四象限,点Q在PA的延长线上,当∠CAQ=∠CBA 45°时,求点P的坐标;(3)、如图②,若点P在第一象限,直线AP交BC于点F,过点P作x轴的垂线交BC于点H,当△PFH为等腰三角形时,求线段PH的长.16. 如图,二次函数 ( 是实数,且 )的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴与 轴交于点 ,已知点 位于第一象限,且在对称轴上, ,点 在 轴的正半轴上, .连接 并延长交 轴于点 ,连接 .
(1)、求抛物线的表达式;(2)、如图①,若点P在第四象限,点Q在PA的延长线上,当∠CAQ=∠CBA 45°时,求点P的坐标;(3)、如图②,若点P在第一象限,直线AP交BC于点F,过点P作x轴的垂线交BC于点H,当△PFH为等腰三角形时,求线段PH的长.16. 如图,二次函数 ( 是实数,且 )的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴与 轴交于点 ,已知点 位于第一象限,且在对称轴上, ,点 在 轴的正半轴上, .连接 并延长交 轴于点 ,连接 . (1)、求 、 、 三点的坐标(用数字或含 的式子表示);(2)、已知点 在抛物线的对称轴上,当 的周长的最小值等于 ,求 的值.17. 如图,在平面直角坐标系中,二次函数 的图像与x轴交于点. 、 ,与y轴交于点C.
(1)、求 、 、 三点的坐标(用数字或含 的式子表示);(2)、已知点 在抛物线的对称轴上,当 的周长的最小值等于 ,求 的值.17. 如图,在平面直角坐标系中,二次函数 的图像与x轴交于点. 、 ,与y轴交于点C.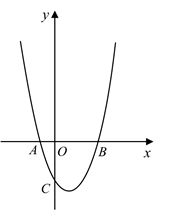 (1)、 , ;(2)、若点D在该二次函数的图象上,且 ,求点D的坐标;(3)、若点P是该二次函数图象上位于x轴上方的一点,且 ,直接写出点P的坐标.18. 如图,抛物线 与x轴交于点A、B,与y轴交于点C,已知 .
(1)、 , ;(2)、若点D在该二次函数的图象上,且 ,求点D的坐标;(3)、若点P是该二次函数图象上位于x轴上方的一点,且 ,直接写出点P的坐标.18. 如图,抛物线 与x轴交于点A、B,与y轴交于点C,已知 .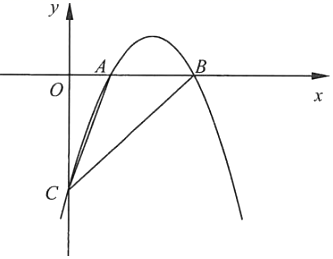 (1)、求m的值和直线 对应的函数表达式;(2)、P为抛物线上一点,若 ,请直接写出点P的坐标;(3)、Q为抛物线上一点,若 ,求点Q的坐标.19. 如图,在平面直角坐标系中,函数 的图像交 轴于点 、 ,交 轴于点 ,它的对称轴交 轴于点 .过点 作 轴交抛物线于点 ,连接 并延长交 轴于点 ,交抛物线于点 .直线 交 于点 ,交抛物线于点 ,连接 、 .
(1)、求m的值和直线 对应的函数表达式;(2)、P为抛物线上一点,若 ,请直接写出点P的坐标;(3)、Q为抛物线上一点,若 ,求点Q的坐标.19. 如图,在平面直角坐标系中,函数 的图像交 轴于点 、 ,交 轴于点 ,它的对称轴交 轴于点 .过点 作 轴交抛物线于点 ,连接 并延长交 轴于点 ,交抛物线于点 .直线 交 于点 ,交抛物线于点 ,连接 、 .

备用图
(1)、点 的坐标为:;(2)、当 是直角三角形时,求 的值;(3)、 与 有怎样的位置关系?请说明理由.20. 如图,二次函数 、 的图像分别为 、 , 交 轴于点 ,点 在 上,且位于 轴右侧,直线 与 在 轴左侧的交点为 . (1)、若 点的坐标为 , 的顶点坐标为 ,求 的值;(2)、设直线 与 轴所夹的角为 .
(1)、若 点的坐标为 , 的顶点坐标为 ,求 的值;(2)、设直线 与 轴所夹的角为 .①当 ,且 为 的顶点时,求 的值;
②若 ,试说明:当 、 、 各自取不同的值时, 的值不变;
(3)、若 ,试判断点 是否为 的顶点?请说明理由.21. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.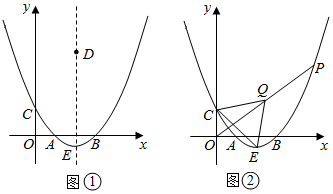 (1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.22. 若二次函数 的图像与x轴有两个交点 ,且经过点 过点A的直线l与x轴交于点 与该函数的图象交于点B(异于点A).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 .
(1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.22. 若二次函数 的图像与x轴有两个交点 ,且经过点 过点A的直线l与x轴交于点 与该函数的图象交于点B(异于点A).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 . (1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.23. 以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题 .
(1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.23. 以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题 .Ⅰ.在 中, ,在探究三边关系时,通过画图,度量和计算,收集到,组数据如下表:(单位:厘米)
2.8
2.7
2.6
2.3
2
1.5
0.4
0.4
0.8
1.2
1.6
2
2.4
2.8
3.2
3.5
3.8
3.9
4
3.9
3.2
Ⅱ.根据学习函数的经验,选取上表中 和 的数据进行分析;
设 ,以 为坐标,在图 所示的坐标系中描出对应的点;
连线;
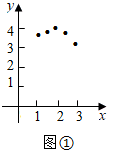
Ⅲ.观察思考
结合表中的数据以及所面的图像,猜想.当 ▲ 时,y最大;
Ⅳ.进一步C猜想:若 中, ,斜边 为常数, ),则 ▲ 时, 最大.
推理证明
Ⅴ.对(4)中的猜想进行证明.
(1)、问题1.在图 中完善(1)的描点过程,并依次连线;(2)、问题2.补全观察思考中的两个猜想:Ⅲ;Ⅳ。(3)、问题3.证明上述Ⅴ中的猜想:(4)、问题4.图 中折线 是一个感光元件的截面设计草图,其中点 间的距离是4厘米, 厘米, 平行光线从 区域射入, 线段 为感光区城,当 的长度为多少时,感光区域长度之和最大,并求出最大值. 24. 在平面直角坐标系中,O为坐标原点,直线 交二次函数 的图像于点A, ,点 在该二次函数的图象上,设过点 (其中 )且平行于 轴的直线交直线 于点M,交直线 于点N,以线段 、 为邻边作矩形 .
24. 在平面直角坐标系中,O为坐标原点,直线 交二次函数 的图像于点A, ,点 在该二次函数的图象上,设过点 (其中 )且平行于 轴的直线交直线 于点M,交直线 于点N,以线段 、 为邻边作矩形 . (1)、若点A的横坐标为8.
(1)、若点A的横坐标为8.①用含m的代数式表示M的坐标;
②点 能否落在该二次函数的图象上?若能,求出m的值;若不能,请说明理由;
(2)、当 时,若点 恰好落在该二次函数的图象上,请直接写出此时满足条件的所有直线 的函数表达式.25. 如图,二次函数 的图像与 轴正半轴交于点A,平行于x轴的直线l与该抛物线交于B、C两点(点B位于点C左侧),与抛物线对称轴交于点 . (1)、求b的值;(2)、设P、Q是x轴上的点(点P位于点Q左侧),四边形 为平行四边形.过点P、Q分别作x轴的垂线,与抛物线交于点 、 .若 ,求 、 的值.26. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.
(1)、求b的值;(2)、设P、Q是x轴上的点(点P位于点Q左侧),四边形 为平行四边形.过点P、Q分别作x轴的垂线,与抛物线交于点 、 .若 ,求 、 的值.26. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.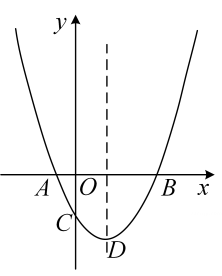
 (1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.27. 如图①,二次函数 的图象与直线l交于 、 两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图象于点N,设点P的横坐标为m.
(1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.27. 如图①,二次函数 的图象与直线l交于 、 两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图象于点N,设点P的横坐标为m.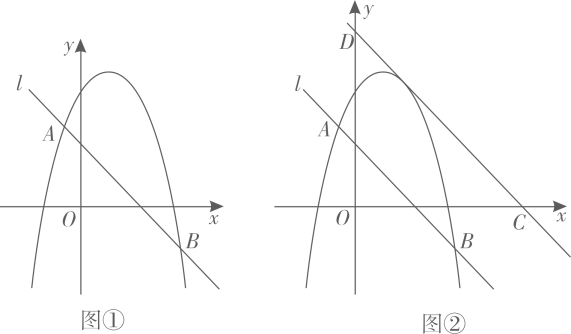 (1)、 , ;(2)、若点N在点M的上方,且 ,求m的值;(3)、将直线 向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).
(1)、 , ;(2)、若点N在点M的上方,且 ,求m的值;(3)、将直线 向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).①记 的面积为 , 的面积为 ,是否存在m,使得点N在直线 的上方,且满足 ?若存在,求出m及相应的 、 的值;若不存在,请说明理由.
②当 时,将线段 绕点M顺时针旋转 得到线段 ,连接 、 、 ,若 ,直接写出直线 与该二次函数图象交点的横坐标.
28. 如图,二次函数 的图像与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点 ,且顶点为D,连接 、 、 、 .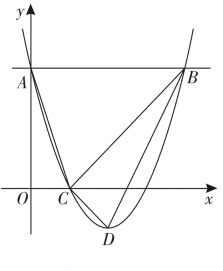
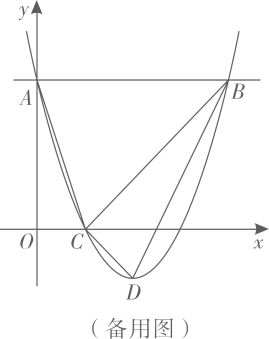 (1)、填空: ;(2)、点P是抛物线上一点,点P的横坐标大于1,直线 交直线 于点Q.若 ,求点P的坐标;(3)、点E在直线 上,点E关于直线 对称的点为F,点F关于直线 对称的点为G,连接 .当点F在x轴上时,直接写出 的长.29. 如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为 ,点D的坐标为 .
(1)、填空: ;(2)、点P是抛物线上一点,点P的横坐标大于1,直线 交直线 于点Q.若 ,求点P的坐标;(3)、点E在直线 上,点E关于直线 对称的点为F,点F关于直线 对称的点为G,连接 .当点F在x轴上时,直接写出 的长.29. 如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为 ,点D的坐标为 . (1)、求该二次函数的表达式;(2)、点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且 ,求点E的坐标.(3)、试问在该二次函数图象上是否存在点G,使得 的面积是 的面积的 ?若存在,求出点G的坐标;若不存在,请说明理由.30. 如图,二次函数 图象的顶点为 ,对称轴是直线 ,一次函数 的图象与 轴交于点 ,且与直线 关于 的对称直线交于点 .
(1)、求该二次函数的表达式;(2)、点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且 ,求点E的坐标.(3)、试问在该二次函数图象上是否存在点G,使得 的面积是 的面积的 ?若存在,求出点G的坐标;若不存在,请说明理由.30. 如图,二次函数 图象的顶点为 ,对称轴是直线 ,一次函数 的图象与 轴交于点 ,且与直线 关于 的对称直线交于点 .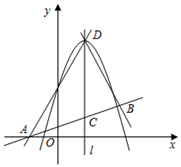 (1)、点 的坐标是;(2)、直线 与直线 交于点 , 是线段 上一点(不与点 、 重合),点 的纵坐标为 .过点 作直线与线段 、 分别交于点 , ,使得 与 相似.
(1)、点 的坐标是;(2)、直线 与直线 交于点 , 是线段 上一点(不与点 、 重合),点 的纵坐标为 .过点 作直线与线段 、 分别交于点 , ,使得 与 相似.①当 时,求 的长;
②若对于每一个确定的 的值,有且只有一个 与 相似,请直接写出 的取值范围.
31. 学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.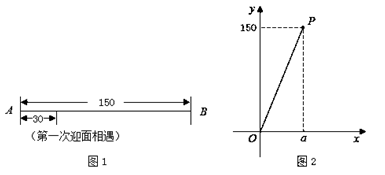 (1)、【观察】
(1)、【观察】①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(2)、【发现】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图 所示).
① =;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
(3)、【拓展】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过 个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是.(直接写出结果)
32. 如图,在平面直角坐标系xOy中,抛物线L1: 过点C(0,﹣3),与抛物线L2: 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.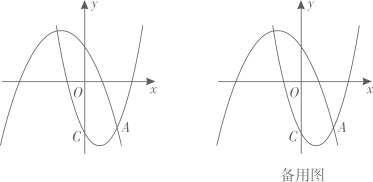 (1)、求抛物线L1对应的函数表达式;(2)、若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;(3)、设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.33. 如图①是一张矩形纸片,按以下步骤进行操作:
(1)、求抛物线L1对应的函数表达式;(2)、若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;(3)、设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.33. 如图①是一张矩形纸片,按以下步骤进行操作: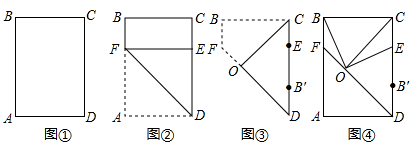
(Ⅰ)将矩形纸片沿DF折叠,使点A落在CD边上点E处,如图②;
(Ⅱ)在第一次折叠的基础上,过点C再次折叠,使得点B落在边CD上点B'处,如图③,两次折痕交于点O;
(Ⅲ)展开纸片,分别连接OB、OE、OC、FD,如图④.
【探究】
(1)、证明:△OBC≌△OED:(2)、若AB=8,设BC为x,OB2为y,求y关于x的关系式.
34. 如图所示・二次函数 的图像与一次函数 的图像交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0. (1)、求A、B两点的横坐标;(2)、若△OAB是以OA为腰的等腰三角形,求k的值;(3)、二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.35. 如图,抛物线 交 轴于 、 两点,其中点 坐标为 ,与 轴交于点 .
(1)、求A、B两点的横坐标;(2)、若△OAB是以OA为腰的等腰三角形,求k的值;(3)、二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.35. 如图,抛物线 交 轴于 、 两点,其中点 坐标为 ,与 轴交于点 .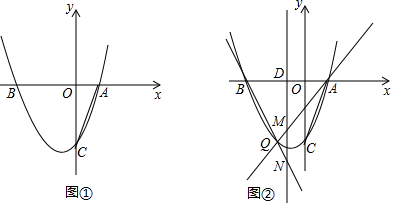 (1)、求抛物线的函数表达式;(2)、如图①,连接 ,点 在抛物线上,且满足 .求点 的坐标;(3)、如图②,点 为 轴下方抛物线上任意一点,点 是抛物线对称轴与 轴的交点,直线 、 分别交抛物线的对称轴于点 、 .请问 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.36. 问题呈现
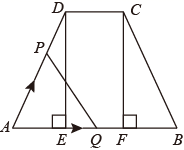
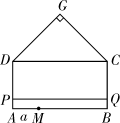
(1)、求抛物线的函数表达式;(2)、如图①,连接 ,点 在抛物线上,且满足 .求点 的坐标;(3)、如图②,点 为 轴下方抛物线上任意一点,点 是抛物线对称轴与 轴的交点,直线 、 分别交抛物线的对称轴于点 、 .请问 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.36. 问题呈现如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°,点M在线段AB上,且AM=a,点P沿折线AD-DG运动,点Q沿折线BC-CG运动(与点G不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.
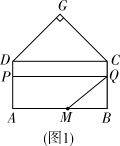
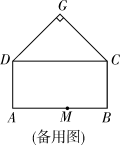
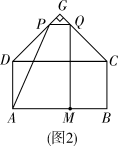 (1)、若a=12.
(1)、若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为;
②在运动过程中,求四边形AMQP的最大面积;
(2)、如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.37. 【概念认识】城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A( , )和B( , ),用以下方式定义两点间距离:d(A,B)= + .
(1)、【数学理解】①已知点A(﹣2,1),则d(O,A)=;②函数 (0≤x≤2)的图像如图①所示,B是图像上一点,d(O,B)=3,则点B的坐标是.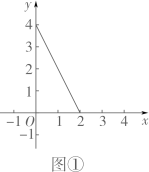 (2)、函数 (x>0)的图像如图②所示,求证:该函数的图象上不存在点C,使d(O,C)=3.
(2)、函数 (x>0)的图像如图②所示,求证:该函数的图象上不存在点C,使d(O,C)=3. (3)、函数 (x≥0)的图像如图③所示,D是图像上一点,求d(O,D)的最小值及对应的点D的坐标.
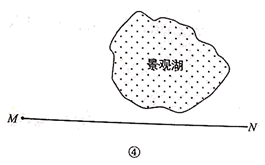
(3)、函数 (x≥0)的图像如图③所示,D是图像上一点,求d(O,D)的最小值及对应的点D的坐标.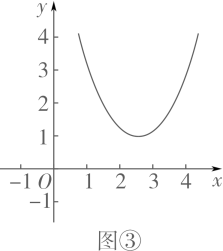 (4)、【问题解决】某市要修建一条通往景观湖的道路,如图④,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边,如何修建能使道路最短?(要求:建立适当的平面直角坐标系,画出示意图并简要说明理由)
(4)、【问题解决】某市要修建一条通往景观湖的道路,如图④,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边,如何修建能使道路最短?(要求:建立适当的平面直角坐标系,画出示意图并简要说明理由)