江苏中考数学历年真题分类卷8 一次函数和反比例函数图像、性质和应用
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、82. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、43. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、4. 已知点 , 在一次函数 的图象上,则 与 的大小关系是( )A、 B、 C、 D、无法确定5. 一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )A、第一 B、第二 C、第三 D、第四6. 点 在函数 的图像上,则代数式 的值等于( )A、5 B、3 C、-3 D、-17. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 小明同学利用计算机软件绘制函数 (a、b为常数)的图像如图所示,由学习函数的经验,可以推断常数a、b的值满足( )
 A、 , B、 , C、 , D、 ,9. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:
A、 , B、 , C、 , D、 ,9. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:①快车途中停留了 ;②快车速度比慢车速度多 ;③图中 ;④快车先到达目的地.其中正确的是( )
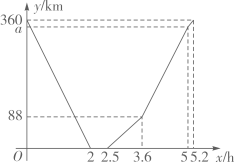 A、①③ B、②③ C、②④ D、①④10. 若 、 都在函数 的图象上,且 ,则( )A、 B、 C、 D、11. 若点P在一次函数 的图像上,则点P一定不在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 若反比例函数 的图像上有两个不同的点关于y轴对称点都在一次函数y=-x+m的图像上,则m的取值范围是( )A、 B、 ① C、 D、13. 如图,已知A为反比例函数 ( <0)的图像上一点,过点A作AB⊥ 轴,垂足为B.若△OAB的面积为2,则k的值为( )
A、①③ B、②③ C、②④ D、①④10. 若 、 都在函数 的图象上,且 ,则( )A、 B、 C、 D、11. 若点P在一次函数 的图像上,则点P一定不在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 若反比例函数 的图像上有两个不同的点关于y轴对称点都在一次函数y=-x+m的图像上,则m的取值范围是( )A、 B、 ① C、 D、13. 如图,已知A为反比例函数 ( <0)的图像上一点,过点A作AB⊥ 轴,垂足为B.若△OAB的面积为2,则k的值为( )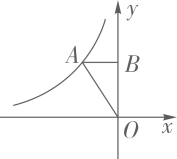 A、2 B、-2 C、4 D、-4
A、2 B、-2 C、4 D、-4二、填空题
-
14. 下表中记录了一次试验中时间和温度的数据.
时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则14分钟时的温度是℃.
15. 请写出一个函数表达式,使其图象在第二、四象限且关于原点对称:.16. 已知一次函数的图象经过点(1,2),且函数值y随自变量x的增大而减小,写出符合条件的一次函数表达式.(答案不唯一,写出一个即可)17. 如图,正比例函数y=k1x和反比例函数y= 图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是.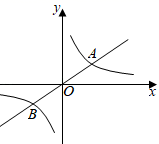 18. 如图,点A、B在反比例函数 的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =.
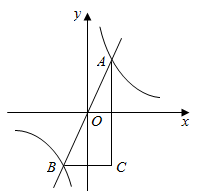
18. 如图,点A、B在反比例函数 的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =. 19. 如图,正比例函数 与函数 的图象交于A,B两点, 轴, 轴,则 .
19. 如图,正比例函数 与函数 的图象交于A,B两点, 轴, 轴,则 .
 20. 若 ,且 ,则 的取值范围为.21. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.22. 如图,点 在反比例函数 的图像上且横坐标为1,过点 作两条坐标轴的平行线,与反比例函数 的图像相交于点 、 ,则直线 与 轴所夹锐角的正切值为.
20. 若 ,且 ,则 的取值范围为.21. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.22. 如图,点 在反比例函数 的图像上且横坐标为1,过点 作两条坐标轴的平行线,与反比例函数 的图像相交于点 、 ,则直线 与 轴所夹锐角的正切值为.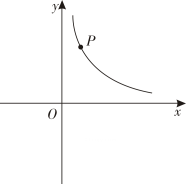 23. 以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为.
23. 以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为. 24. 若一次函数 的图像与 轴交于点 ,则 .25. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 .
24. 若一次函数 的图像与 轴交于点 ,则 .25. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 . 26. 将一次函数 的图象绕原点O逆时针旋转 ,所得到的图像对应的函数表达式是.27. 如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为.
26. 将一次函数 的图象绕原点O逆时针旋转 ,所得到的图像对应的函数表达式是.27. 如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为.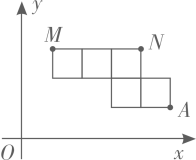 28. 若一次函数 y=kx+2 的函数值y随自变量x增大而增大,则实数k的取值范围是.29. 平面直角坐标系中,点 到原点的距离是.30. 如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是.
28. 若一次函数 y=kx+2 的函数值y随自变量x增大而增大,则实数k的取值范围是.29. 平面直角坐标系中,点 到原点的距离是.30. 如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是. 31. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为.
31. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为.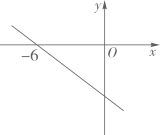
三、解答题
-
32. 如图,在平面直角坐标系中.四边形 为矩形,点 、 分别在 轴和 轴的正半轴上,点 为 的中点已知实数 ,一次函数 的图象经过点 、 ,反比例函数 的图象经过点 ,求 的值.
四、综合题
-
33. 如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.
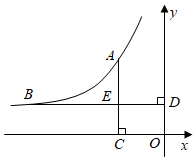 (1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).34. A,B两家超市平时以同样的价格出售相同的商品.暑假期间两家超市都进行促销活动,促销方式如下:
(1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).34. A,B两家超市平时以同样的价格出售相同的商品.暑假期间两家超市都进行促销活动,促销方式如下:A超市:一次购物不超过300元的打9折,超过300元后的价格部分打7折;
B超市:一次购物不超过100元的按原价,超过100元后的价格部分打8折.
例如,一次购物的商品原价为500元,
去A超市的购物金额为: (元);
去B超市的购物金额为: (元).
(1)、设商品原价为x元,购物金额为y元,分别就两家超市的促销方式写出y关于x的函数解析式;(2)、促销期间,若小刚一次购物的商品原价超过200元,他去哪家超市购物更省钱?请说明理由.35. 如图,在平面直角坐标系 中,一次函数 的图象分别与x轴、y轴交于点A、B,与反比例函数 的图象交于点C,连接 .已知点 , . (1)、求b、k的值;(2)、求 的面积.36. 如图,点A和点E(2,1)是反比例函数y= (x>0)图象上的两点,点B在反比例函数y= (x<0)的图象上,分别过点A,B作y轴的垂线,垂足分别为点C,D,AC=BD,连接AB交y轴于点F.
(1)、求b、k的值;(2)、求 的面积.36. 如图,点A和点E(2,1)是反比例函数y= (x>0)图象上的两点,点B在反比例函数y= (x<0)的图象上,分别过点A,B作y轴的垂线,垂足分别为点C,D,AC=BD,连接AB交y轴于点F.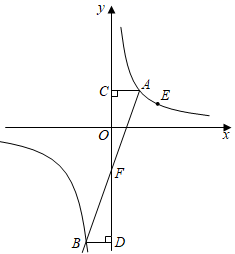 (1)、k=;(2)、设点A的横坐标为a,点F的纵坐标为m,求证:am=﹣2;(3)、连接CE,DE,当∠CED=90°时,直接写出点A的坐标:.37. 甲、乙两人沿同一直道从A地去B地,甲比乙早 出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离 (单位:m)与时间x(单位: )之间的函数关系如图所示.
(1)、k=;(2)、设点A的横坐标为a,点F的纵坐标为m,求证:am=﹣2;(3)、连接CE,DE,当∠CED=90°时,直接写出点A的坐标:.37. 甲、乙两人沿同一直道从A地去B地,甲比乙早 出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离 (单位:m)与时间x(单位: )之间的函数关系如图所示. (1)、在图中画出乙离A地的距离 (单位:m)与时间x之间的函数图;(2)、若甲比乙晚 到达B地,求甲整个行程所用的时间.38. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.
(1)、在图中画出乙离A地的距离 (单位:m)与时间x之间的函数图;(2)、若甲比乙晚 到达B地,求甲整个行程所用的时间.38. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.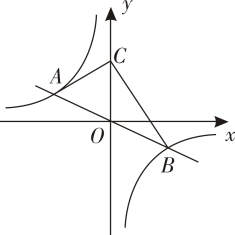 (1)、n= , k=;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.39. 如图,已知线段 ,点 在平面直角坐标系 内,
(1)、n= , k=;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.39. 如图,已知线段 ,点 在平面直角坐标系 内,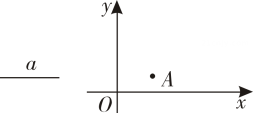 (1)、用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.40. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
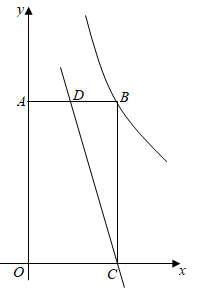
(1)、用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.40. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.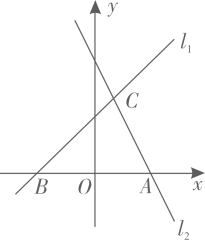 (1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.41. 如图,已知点 、 ,点P为线段AB上的一个动点,反比例函数 的图像经过点P.小明说:“点P从点A运动至点B的过程中,k值逐渐增大,当点P在点A位置时k值最小,在点B位置时k值最大.”
(1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.41. 如图,已知点 、 ,点P为线段AB上的一个动点,反比例函数 的图像经过点P.小明说:“点P从点A运动至点B的过程中,k值逐渐增大,当点P在点A位置时k值最小,在点B位置时k值最大.”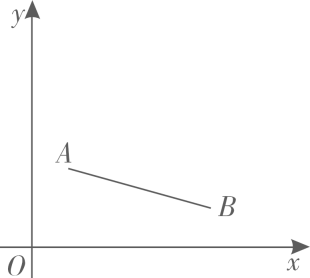 (1)、当 时.
(1)、当 时.①求线段AB所在直线的函数表达式.
②你完全同意小明的说法吗?若完全同意,请说明理由;若不完全同意,也请说明理由,并求出正确的k的最小值和最大值.
(2)、若小明的说法完全正确,求n的取值范围.42. 某商店代理销售一种水果,六月份的销售利润y(元)与销售量 之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
日期
销售记录
6月1日
库存 ,成本价8元/ ,售价10元/ (除了促销降价,其他时间售价保持不变).
6月9日
从6月1日至今,一共售出 .
6月10、11日
这两天以成本价促销,之后售价恢复到10元/ .
6月12日
补充进货 ,成本价8.5元/ .
6月30日
水果全部售完,一共获利1200元.
(1)、截止到6月9日,该商店销售这种水果一共获利多少元?(2)、求图像中线段 所在直线对应的函数表达式.43. 如图,在平面直角坐标系 中,反比例函数 的图像经过点 ,点B在y轴的负半轴上, 交x轴于点C,C为线段 的中点.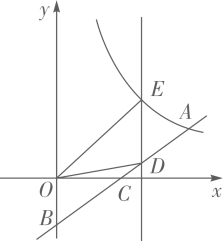 (1)、 , 点 的坐标为;(2)、若点D为线段 上的一个动点,过点D作 轴,交反比例函数图象于点E,求 面积的最大值.44. 甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为 千米,图中折线 表示接到通知前y与x之间的函数关系.
(1)、 , 点 的坐标为;(2)、若点D为线段 上的一个动点,过点D作 轴,交反比例函数图象于点E,求 面积的最大值.44. 甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为 千米,图中折线 表示接到通知前y与x之间的函数关系. (1)、根据图象可知,休息前汽车行驶的速度为千米/小时;(2)、求线段 所表示的y与x之间的函数表达式;(3)、接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.45. 小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于 ,超过 时,所有这种水果的批发单价均为3元 .图中折线表示批发单价 (元 )与质量 的函数关系.
(1)、根据图象可知,休息前汽车行驶的速度为千米/小时;(2)、求线段 所表示的y与x之间的函数表达式;(3)、接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.45. 小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于 ,超过 时,所有这种水果的批发单价均为3元 .图中折线表示批发单价 (元 )与质量 的函数关系. (1)、求图中线段 所在直线的函数表达式;(2)、小李用800元一次可以批发这种水果的质量是多少?46. 快车从甲地驶向乙地,慢车从乙地驶向甲地,两车同时出发并且在同一条公路上匀速行驶,途中快车休息1.5小时,慢车没有休息.设慢车行驶的时间为x小时,快车行驶的路程为 千米,慢车行驶的路程为 千米.如图中折线OAEC表示 与x之间的函数关系,线段OD表示 与x之间的函数关系.
(1)、求图中线段 所在直线的函数表达式;(2)、小李用800元一次可以批发这种水果的质量是多少?46. 快车从甲地驶向乙地,慢车从乙地驶向甲地,两车同时出发并且在同一条公路上匀速行驶,途中快车休息1.5小时,慢车没有休息.设慢车行驶的时间为x小时,快车行驶的路程为 千米,慢车行驶的路程为 千米.如图中折线OAEC表示 与x之间的函数关系,线段OD表示 与x之间的函数关系.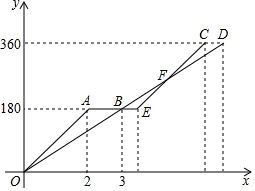
请解答下列问题:
(1)、求快车和慢车的速度;(2)、求图中线段EC所表示的 与x之间的函数表达式;(3)、线段OD与线段EC相交于点F,直接写出点F的坐标,并解释点F的实际意义.47. 如图,点 和点 是反比例函数 图象上的两点,一次函数 的图象经过点 ,与 轴交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,连接 .已知 与 的面积满足 . (1)、 = , = ;(2)、已知点 在线段 上,当 时,求点 的坐标.48. 如图,在平面直角坐标系xOy中,函数 的图像与函数 (x<0)的图像相交于点A(﹣1,6),并与x轴交于点C.点D是线段AC上一点,△ODC与△OAC的面积比为2:3.
(1)、 = , = ;(2)、已知点 在线段 上,当 时,求点 的坐标.48. 如图,在平面直角坐标系xOy中,函数 的图像与函数 (x<0)的图像相交于点A(﹣1,6),并与x轴交于点C.点D是线段AC上一点,△ODC与△OAC的面积比为2:3.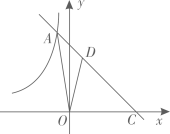 (1)、k= , b=;(2)、求点D的坐标;(3)、若将△ODC绕点O逆时针旋转,得到△OD′C′,其中点D′落在x轴负半轴上,判断点C′是否落在函数 (x<0)的图像上,并说明理由.49. “低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑车前往乙地,她与乙地之间的距离y(km)与出发时间之间的函数关系式如图1中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离S(km)与出发时间x(h)之间的函数关系式如图2中折线段CD-DE-EF所示.
(1)、k= , b=;(2)、求点D的坐标;(3)、若将△ODC绕点O逆时针旋转,得到△OD′C′,其中点D′落在x轴负半轴上,判断点C′是否落在函数 (x<0)的图像上,并说明理由.49. “低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑车前往乙地,她与乙地之间的距离y(km)与出发时间之间的函数关系式如图1中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离S(km)与出发时间x(h)之间的函数关系式如图2中折线段CD-DE-EF所示. (1)、小丽和小明骑车的速度各是多少?(2)、求E点坐标,并解释点的实际意义.50. 已知一次函数 (k为常数,k≠0)和 .(1)、当k=﹣2时,若 > ,求x的取值范围;(2)、当x<1时, > .结合图像,直接写出k的取值范围.
(1)、小丽和小明骑车的速度各是多少?(2)、求E点坐标,并解释点的实际意义.50. 已知一次函数 (k为常数,k≠0)和 .(1)、当k=﹣2时,若 > ,求x的取值范围;(2)、当x<1时, > .结合图像,直接写出k的取值范围.
-