江苏中考数学历年真题分类卷9 二次函数图像、性质及应用

试卷更新日期：2021-09-27 类型：二轮复习

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，将二次函数 $y = x^{2}$ 的图象向左平移2个单位长度，再向上平移1个单位长度，所得抛物线对应的函数表达式为（）

A、 $y = {(x - 2)}^{2} + 1$ B、 $y = {(x + 2)}^{2} + 1$ C、 $y = {(x + 2)}^{2} - 1$ D、 $y = {(x - 2)}^{2} - 1$

查看试题解析
2. 已知二次函数 $y = (a - 1) x^{2}$ ，当 $x > 0$ 时，y随x增大而增大，则实数a的取值范围是（）

A、 $a > 0$ B、 $a > 1$ C、 $a \neq 1$ D、 $a < 1$

查看试题解析
3. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，有下列结论：① $a > 0$ ；② $b^{2} - 4 a c$ ＞0；③ $4 a + b = 0$ ；④不等式 $a x^{2} + （ b - 1 ） x + c$ ＜0的解集为1≤x＜3，正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析
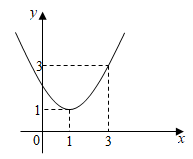4. 已知抛物线 $y = x^{2} + k x - k^{2}$ 的对称轴在 $y$ 轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则 $k$ 的值是（）

A、-5或2 B、-5 C、2 D、-2

查看试题解析
5. 点P(m，n)在以y轴为对称轴的二次函数y＝x²+ax+4的图象上.则m﹣n的最大值等于（）

A、 $\frac{15}{4}$ B、4 C、﹣ $\frac{15}{4}$ D、﹣ $\frac{17}{4}$

查看试题解析
6. 将二次函数y=(x﹣1)²+2的图象向上平移3个单位长度，得到的拋物线相应的函数表达式为（）

A、y=(x+2)²﹣2 B、y=(x﹣4)²+2 C、y=(x﹣1)²﹣1 D、y=(x﹣1)²+5

查看试题解析
7. 如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°.若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（）

A、18m² B、 $18 \sqrt{3}$ m² C、 $24 \sqrt{3}$ m² D、 $\frac{45 \sqrt{3}}{2}$ m²

查看试题解析

二、填空题

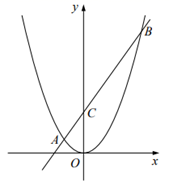
8. 在函数 $y = {(x - 1)}^{2}$ 中，当x＞1时，y随x的增大而 .（填“增大”或“减小”）

查看试题解析
9. 如图，在平面直角坐标系中，O为坐标原点，点C为y轴正半轴上的一个动点，过点C的直线与二次函数 $y = x^{2}$ 的图象交于A、B两点，且 $C B = 3 A C$ ，P为 $C B$ 的中点，设点P的坐标为 $P (x ， y) (x > 0)$ ，写出y关于x的函数表达式为：.

查看试题解析
10. 某快餐店销售A、B两种快餐，每份利润分别为12元、8元，每天卖出份数分别为40份、80份.该店为了增加利润，准备降低每份A种快餐的利润，同时提高每份B种快餐的利润.售卖时发现，在一定范围内，每份A种快餐利润每降1元可多卖2份，每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变，那么这两种快餐一天的总利润最多是元.

查看试题解析
11. 请写出一个函数表达式，使其图象的对称轴为 $y$ 轴：.

查看试题解析
12. 二次函数 $y = a x^{2} - 3 a x + 3$ 的图像过点 $A (6 ， 0)$ ，且与y轴交于点B，点M在该抛物线的对称轴上，若 $Δ A B M$ 是以 $A B$ 为直角边的直角三角形，则点M的坐标为.

查看试题解析
13. 平面直角坐标系 $x O y$ 中，已知点 $P (m ， 3 n^{2} - 9)$ ，且实数m，n满足 $m - n^{2} + 4 = 0$ ，则点P到原点O的距离的最小值为.

查看试题解析
14. 下列关于二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ （ $m$ 为常数）的结论，①该函数的图象与函数 $y = - x^{2}$ 的图象形状相同；②该函数的图象一定经过点 $(0 ， 1)$ ；③当 $x > 0$ 时，y随x的增大而减小；④该函数的图象的顶点在函数 $y = x^{2} + 1$ 的图像上，其中所有正确的结论序号是.

查看试题解析
15. 加工爆米花时，爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下，可食用率 $y$ 与加工时间 $x$ （单位： $\min$ ）满足函数表达式 $y = - 0.2 x^{2} + 1.5 x - 2$ ，则最佳加工时间为 $\min$ .

查看试题解析
16. 已知抛物线 $y = a x^{2} + 4 a x + 4 a + 1 (a \neq 0)$ 过点 $A (m ， 3)$ ， $B (n ， 3)$ 两点，若线段 $A B$ 的长不大于 $4$ ，则代数式 $a^{2} + a + 1$ 的最小值是.

查看试题解析

三、综合题

17. 农技人员对培育的某一品种桃树进行研究，发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x（个）为横坐标、桃子的平均质量y（克/个）为纵坐标，在平面直角坐标系中描出对应的点，发现这些点大致分布在直线AB附近（如图所示）.

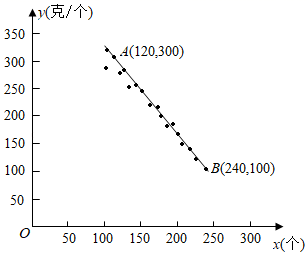(1)、求直线AB的函数关系式；

(2)、市场调研发现：这个品种每个桃子的平均价格w（元）与平均质量y（克/个）满足函数表达式w＝ $\frac{1}{100}$ y+2.在（1）的情形下，求一棵树上桃子数量为多少时，该树上的桃子销售额最大？

查看试题解析
18. 已知抛物线 $y = a {(x - 1)}^{2} + h$ 经过点 $(0 ， - 3)$ 和 $(3 ， 0)$ .

(1)、求 $a$ 、 $h$ 的值；

(2)、将该抛物线向上平移2个单位长度，再向右平移1个单位长度，得到新的抛物线，直接写出新的抛物线相应的函数表达式.

查看试题解析
19. 某超市经销一种商品，每件成本为50元.经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件.设该商品每件的销售价为x元，每个月的销售量为y件.

(1)、求y与x的函数表达式；

(2)、当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？

查看试题解析
20. 已知二次函数 $y = a x^{2} + b x + c$ 的图象经过 $(- 2 ， 1) ， (2 ， - 3)$ 两点.

(1)、求b的值.

(2)、当 $c > - 1$ 时，该函数的图象的顶点的纵坐标的最小值是.

(3)、设 $(m ， 0)$ 是该函数的图象与x轴的一个公共点，当 $- 1 < m < 3$ 时，结合函数的图象，直接写出a的取值范围.

查看试题解析

21. 甲、乙两汽车出租公司均有50辆汽车对外出租，下面是两公司经理的一段对话：

甲公司经理：如果我公司每辆汽车月租费3000元，那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元，那么将少租出1辆汽车.另外，公司为每辆租出的汽车支付月维护费200元.

乙公司经理：我公司每辆汽车月租费3500元，无论是否租出汽车，公司均需一次性支付月维护费共计1850元.

说明：①汽车数量为整数；

②月利润=月租车费-月维护费；

③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润.

在两公司租出的汽车数量相等的条件下，根据上述信息，解决下列问题：

(1)、当每个公司租出的汽车为10辆时，甲公司的月利润是元；当每个公司租出的汽车为辆时，两公司的月利润相等；

(2)、求两公司月利润差的最大值；

(3)、甲公司热心公益事业，每租出1辆汽车捐出a元

(a > 0)

给慈善机构，如果捐款后甲公司剩余的月利润仍高于乙公司月利润，且当两公司租出的汽车均为17辆时，甲公司剩余的月利润与乙公司月利润之差最大，求a的取值范围.

查看试题解析

22. 如图在平面直角坐标系中，一次函数 $y = k x + b$ 的图像经过点 $A (0 ， - 4)$ 、 $B (2 ， 0)$ 交反比例函数 $y = \frac{m}{x}$ $(x > 0)$ 的图像于点 $C (3 ， a)$ ，点 $P$ 在反比例函数的图象上，横坐标为 $n$ $(0 < n < 3)$ ， $P Q / / y$ 轴交直线 $A B$ 于点 $Q$ ， $D$ 是 $y$ 轴上任意一点，连接 $P D$ 、 $Q D$ .

(1)、求一次函数和反比例函数的表达式；

(2)、求 $△ D P Q$ 面积的最大值.

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ， $P$ 为 $B C$ 边上的动点（与 $B$ 、 $C$ 不重合）， $P D // A B$ ，交 $A C$ 于点 $D$ ，连接 $A P$ ，设 $C P = x$ ， $△ A D P$ 的面积为 $S$ .

(1)、用含 $x$ 的代数式表示 $A D$ 的长；

(2)、求 $S$ 与 $x$ 的函数表达式，并求当 $S$ 随 $x$ 增大而减小时 $x$ 的取值范围.

查看试题解析
24. 某超市经销一种商品，每千克成本为50元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如下表所示：

销售单价x（元/千克）

55

60

65

70

销售量y（千克）

70

60

50

40

(1)、求y（千克）与x（元/千克）之间的函数表达式；

(2)、为保证某天获得600元的销售利润，则该天的销售单价应定为多少？

(3)、当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？

查看试题解析
25. 已知抛物线y＝ax²+bx+c经过A（2，0），B（3n﹣4，y₁），C（5n+6，y₂）三点，对称轴是直线x＝1.关于x的方程ax²+bx+c＝x有两个相等的实数根.

(1)、求抛物线的解析式；

(2)、若n＜﹣5，试比较y₁与y₂的大小；

(3)、若B，C两点在直线x＝1的两侧，且y₁＞y₂ ，求n的取值范围.

查看试题解析
26. 有一块矩形地块 $A B C D$ ， $A B = 20$ 米， $B C = 30$ 米，为美观，拟种植不同的花卉，如图所示，将矩形 $A B C D$ 分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x米.现决定在等腰梯形 $A E H D$ 和 $B C G F$ 中种植甲种花卉；在等腰梯形 $A B F E$ 和 $C D H G$ 中种植乙种花卉；在矩形 $E F G H$ 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米 $^{2}$ 、60 元/米 $^{2}$ 、40元/米 $^{2}$ ，设三种花卉的种植总成本为y元.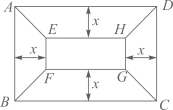

(1)、当 $x = 5$ 时，求种植总成本y；

(2)、求种植总成本y与x的函数表达式，并写出自变量x的取值范围；

(3)、若甲、乙两种花卉的种植面积之差不超过120米 $^{2}$ ，求三种花卉的最低种植总成本.

查看试题解析
27. 小明和小丽先后从A地出发同一直道去B地，设小丽出发第 $x \min$ 时，小丽、小明离B地的距离分别为 $y {}_{1}m$ 、 $y {}_{2}m$ ， $y_{1}$ 与x之间的数表达式 $y_{1} = - 180 x + 2250$ ， $y_{2}$ 与x之间的函数表达式是 $y_{2} = - 10 x^{2} - 100 x + 2000$ .

(1)、小丽出发时，小明离A地的距离为 $m$ .

(2)、小丽发至小明到达B地这段时间内，两人何时相距最近？最近距离是多少？

查看试题解析
28. 如图，在平面直角坐标系 $x O y$ 中，二次函数图象的顶点坐标为 $(4 ， - 3)$ ，该图象与 $x$ 轴相交于点 $A$ 、 $B$ ，与 $y$ 轴相交于点 $C$ ，其中点 $A$ 的横坐标为1．

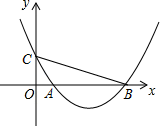(1)、求该二次函数的表达式；

(2)、求 $\tan ∠ A B C$ ．

查看试题解析
29. 如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点 $A$ .甲从中山路上点 $B$ 出发，骑车向北匀速直行；与此同时，乙从点 $A$ 出发，沿北京路步行向东匀速直行.设出发 $x \min$ 时，甲、乙两人与点 $A$ 的距离分别为 $y_{1} m$ 、 $y_{2} m$ .已知 $y_{1}$ 、 $y_{2}$ 与 $x$ 之间的函数关系如图②所示.

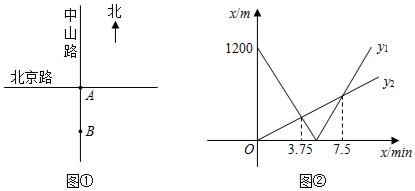(1)、求甲、乙两人的速度；

(2)、当 $x$ 取何值时，甲、乙两人之间的距离最短？

查看试题解析
30. 已知：二次函数 $y = x^{2} - 4 x + 3 a + 2$ (a为常数).

(1)、请写出该二次函数图象的三条性质；

(2)、在同一直角坐标系中，若该二次函数的图象在 $x \leq 4$ 的部分与一次函数 $y = 2 x - 1$ 的图象有两个交点，求 $a$ 的取值范围.

查看试题解析
31. 超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件.根据市场调查发现，销售单价每增加2元，每天销售量会减少1件.设销售单价增加 $x$ 元，每天售出 $y$ 件.

(1)、请写出 $y$ 与 $x$ 之间的函数表达式；

(2)、当 $x$ 为多少时，超市每天销售这种玩具可获利润2250元？

(3)、设超市每天销售这种玩具可获利 $w$ 元，当 $x$ 为多少时 $w$ 最大，最大值是多少？

查看试题解析
32. 已知二次函数 $y = a x^{2} + b x - 4$ （a＞0）的图象与x轴交于A、B两点，（A在B左侧，且OA＜OB），与y轴交于点C.

(1)、求C点坐标，并判断b的正负性；

(2)、设这个二次函数的图象的对称轴与直线AC交于点D，已知DC：CA=1：2，直线BD与y轴交于点E，连接BC，
①若△BCE的面积为8，求二次函数的解析式；

②若△BCD为锐角三角形，请直接写出OA的取值范围.

查看试题解析
33. 定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”.例如，点 $(1 ， 1)$ 是函数 $y = \frac{1}{2} x + \frac{1}{2}$ 的图象的“等值点”.

(1)、分别判断函数 $y = x + 2 ， y = x^{2} - x$ 的图象上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；

(2)、设函数 $y = \frac{3}{x} (x > 0) ， y = - x + b$ 的图象的“等值点”分别为点A，B，过点B作 $B C ⊥ x$ 轴，垂足为C.当 $△ A B C$ 的面积为3时，求b的值；

(3)、若函数 $y = x^{2} - 2 (x \geq m)$ 的图象记为 $W_{1}$ ，将其沿直线 $x = m$ 翻折后的图象记为 $W_{2}$ .当 $W_{1} ， W_{2}$ 两部分组成的图象上恰有2个“等值点”时，直接写出m的取值范围.

查看试题解析
34. 如图，点 $A ， B$ 在函数 $y = \frac{1}{4} x^{2}$ 的图象上.已知 $A ， B$ 的横坐标分别为－2、4，直线 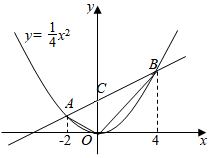$A B$ 与 $y$ 轴交于点 $C$ ，连接 $O A ， O B$ .

(1)、求直线 $A B$ 的函数表达式；

(2)、求 $Δ A O B$ 的面积；

(3)、若函数 $y = \frac{1}{4} x^{2}$ 的图象上存在点 $P$ ，使得 $Δ P A B$ 的面积等于 $Δ A O B$ 的面积的一半，则这样的点 $P$ 共有个.

查看试题解析
35. 二次函数y＝﹣x²+（a﹣1）x+a（a为常数）图象的顶点在y轴右侧.

(1)、写出该二次函数图象的顶点横坐标（用含a的代数式表示）；

(2)、该二次函数表达式可变形为y＝﹣（x﹣p）（x﹣a）的形式，求p的值；

(3)、若点A（m，n）在该二次函数图象上，且n＞0，过点（m+3，0）作y轴的平行线，与二次函数图象的交点在x轴下方，求a的范围.

查看试题解析

销售单价x（元/千克）	55	60	65	70
销售量y（千克）	70	60	50	40