江苏中考数学历年真题分类卷10 锐角三角函数
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
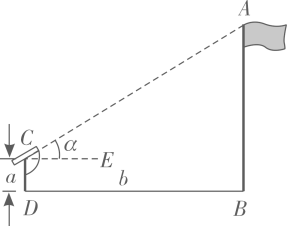 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
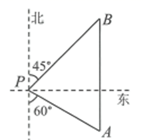
2. 如图,一艘轮船位于灯塔P的南偏东 方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东 方向上的B处,此时B处与灯塔P的距离为海里(结果保留根号).
 3. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.4. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
3. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.4. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 5. 如图,无人机于空中 处测得某建筑顶部 处的仰角为 ,测得该建筑底部 处的俯角为 .若无人机的飞行高度 为 ,则该建筑的高度 为 .(参考数据: , , )
5. 如图,无人机于空中 处测得某建筑顶部 处的仰角为 ,测得该建筑底部 处的俯角为 .若无人机的飞行高度 为 ,则该建筑的高度 为 .(参考数据: , , )
三、解答题
-
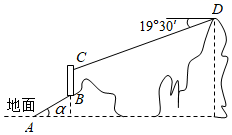
6. 如图,游客从旅游景区山脚下的地面A处出发,沿坡角α=30°的斜坡AB步行50m至山坡B处,乘直立电梯上升30m至C处,再乘缆车沿长为180m的索道CD至山顶D处,此时观测C处的俯角为19°30′,索道CD看作在一条直线上.求山顶D的高度.(精确到1m,sin19°30′≈0.33,cos19°30′≈0.94,tan19°30′≈0.35)
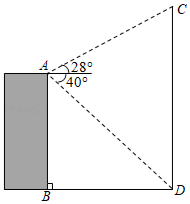
 7. 如图,平地上一幢建筑物AB与铁塔CD相距50m,在建筑物的顶部A处测得铁塔顶部C的仰角为28°、铁塔底部D的俯角为40°,求铁塔CD的高度.
7. 如图,平地上一幢建筑物AB与铁塔CD相距50m,在建筑物的顶部A处测得铁塔顶部C的仰角为28°、铁塔底部D的俯角为40°,求铁塔CD的高度.(参考数据:sin28°≈0.47,cos28°≈0.8,tan28°≈0.53,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
 8. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据: 1.414, =1.732).
8. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据: 1.414, =1.732).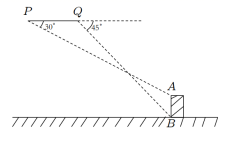 9. 如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得 , , , , ,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据: .)
9. 如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得 , , , , ,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据: .)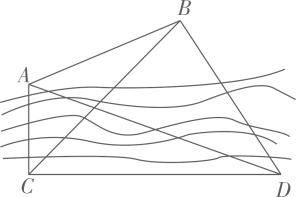 10. 小红和爸爸绕着小区广场锻炼如图在矩形广场 边 的中点 处有一座雕塑.在某一时刻,小红到达点 处,爸爸到达点 处,此时雕塑在小红的南偏东 方向,爸爸在小红的北偏东 方向,若小红到雕塑的距离 ,求小红与爸爸的距离 .(结果精确到 ,参考数据: , , )
10. 小红和爸爸绕着小区广场锻炼如图在矩形广场 边 的中点 处有一座雕塑.在某一时刻,小红到达点 处,爸爸到达点 处,此时雕塑在小红的南偏东 方向,爸爸在小红的北偏东 方向,若小红到雕塑的距离 ,求小红与爸爸的距离 .(结果精确到 ,参考数据: , , )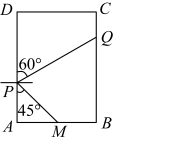 11. 如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
11. 如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)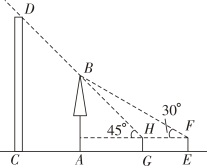 12. 我市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面 的 处测得在 处的龙舟俯角为 ;他登高 到正上方的 处测得驶至 处的龙舟俯角为 ,问两次观测期间龙舟前进了多少?(结果精确到 ,参考数据: , , , )
12. 我市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面 的 处测得在 处的龙舟俯角为 ;他登高 到正上方的 处测得驶至 处的龙舟俯角为 ,问两次观测期间龙舟前进了多少?(结果精确到 ,参考数据: , , , ) 13. 如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从观测站A测得船C在北偏东45°的方向,从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.
13. 如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从观测站A测得船C在北偏东45°的方向,从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.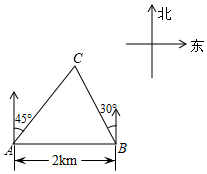 14. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )
14. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )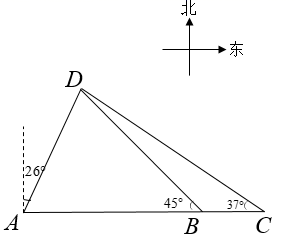 15. 如图,山顶有一塔AB,塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°,从与F点相距50m的D处测得A的仰角为45°.求隧道EF的长度.(参考数据:tan22°≈0.40,tan27°≈0.51)
15. 如图,山顶有一塔AB,塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°,从与F点相距50m的D处测得A的仰角为45°.求隧道EF的长度.(参考数据:tan22°≈0.40,tan27°≈0.51)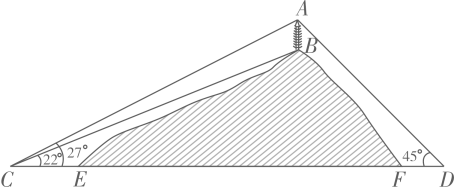
四、综合题
-
16. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .
参考数据:
三角函数锐角
13°
28°
32°
0.22
0.47
0.53
0.97
0.88
0.85
0.23
0.53
0.62
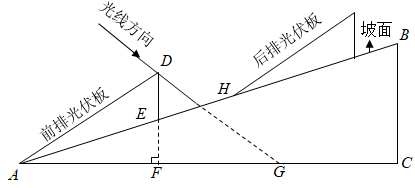 (1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?17. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?17. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .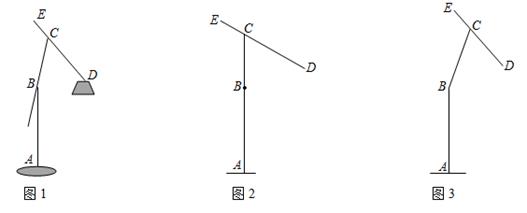 (1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )18. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )18. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .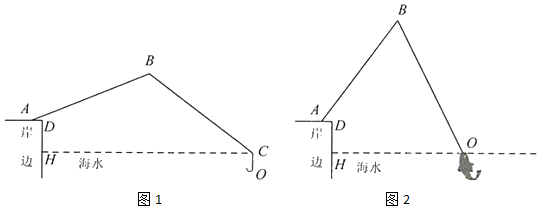 (1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )19. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
(1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )19. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
 (1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )20. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .
(1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )20. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .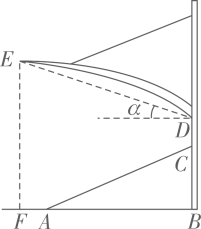
求:
(1)、观众区的水平宽度 ;(2)、顶棚的 处离地面的高度 .( , ,结果精确到 )21. 【材料阅读】地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图 中的 ).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图 所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角 的大小是变化的.
【实际应用】观测点 在图1所示的 上,现在利用这个工具尺在点 处测得 为 ,在点 所在子午线往北的另一个观测点 ,用同样的工具尺测得 为 . 是 的直径, .
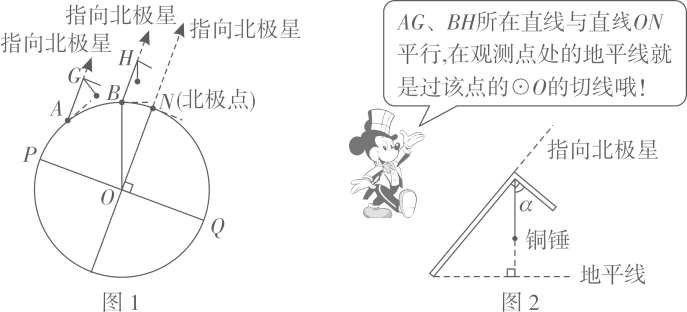 (1)、求 的度数;(2)、已知 km,求这两个观测点之间的距离即 上 的长.( 取 )22. 在三角形纸片 (如图1)中, , .小霞用 张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2).
(1)、求 的度数;(2)、已知 km,求这两个观测点之间的距离即 上 的长.( 取 )22. 在三角形纸片 (如图1)中, , .小霞用 张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2).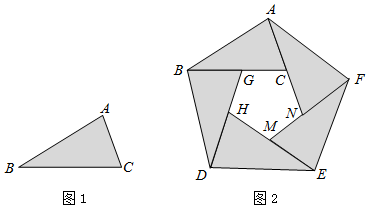 (1)、 °;(2)、求正五边形 的边 的长.参考值: , , .23. 如图,海上观察哨所B位于观察哨所A正北方向,距离为25海里.在某时刻,哨所A与哨所B同时发现一走私船,其位置C位于哨所A北偏东53°的方向上,位于哨所B南偏东37°的方向上.
(1)、 °;(2)、求正五边形 的边 的长.参考值: , , .23. 如图,海上观察哨所B位于观察哨所A正北方向,距离为25海里.在某时刻,哨所A与哨所B同时发现一走私船,其位置C位于哨所A北偏东53°的方向上,位于哨所B南偏东37°的方向上.(参考数据:sin37°=cos53°≈,cos37 =sin53°≈去,tan37°≈2,tan76°≈)
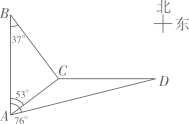 (1)、求观察哨所A与走私船所在的位置C的距离;(2)、若观察哨所A发现走私船从C处以16海里/小时的速度向正东方向逃窜,并立即派缉私艇沿北偏东76°的方向前去拦截.求缉私艇的速度为多少时,恰好在D处成功拦截.(结果保留根号)24. 宿迁市政府为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图,其中 、 都与地面l平行,车轮半径为 , , ,坐垫 与点 的距离 为 .
(1)、求观察哨所A与走私船所在的位置C的距离;(2)、若观察哨所A发现走私船从C处以16海里/小时的速度向正东方向逃窜,并立即派缉私艇沿北偏东76°的方向前去拦截.求缉私艇的速度为多少时,恰好在D处成功拦截.(结果保留根号)24. 宿迁市政府为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图,其中 、 都与地面l平行,车轮半径为 , , ,坐垫 与点 的距离 为 .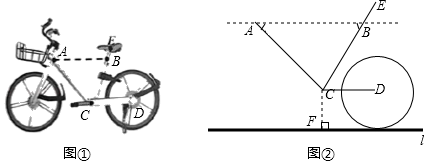 (1)、求坐垫 到地面的距离;(2)、根据经验,当坐垫 到 的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长.
(1)、求坐垫 到地面的距离;(2)、根据经验,当坐垫 到 的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长.(结果精确到 ,参考数据: , , )
-