江苏中考数学历年真题分类卷12 几何综合题和压轴题
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 如图①,AB=5,射线AM∥BN,点C在射线BN上,将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上,点P,Q分别在射线AM、BN上,PQ∥AB.设AP=x,QD=y.若y关于x的函数图象(如图②)经过点E(9,2),则cosB的值等于( )
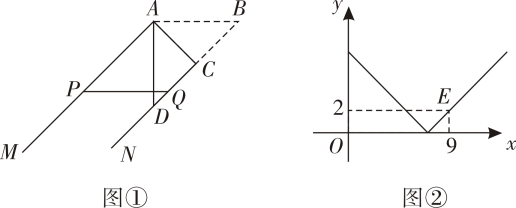 A、 B、 C、 D、2. 如图,等边 的边长为3,点D在边 上, ,线段 在边 上运动, ,有下列结论:
A、 B、 C、 D、2. 如图,等边 的边长为3,点D在边 上, ,线段 在边 上运动, ,有下列结论:
① 与 可能相等;② 与 可能相似;③四边形 面积的最大值为 ;④四边形 周长的最小值为 .其中,正确结论的序号为( )
A、①④ B、②④ C、①③ D、②③3. 如图,菱形 的顶点 、 在 轴上( 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于( )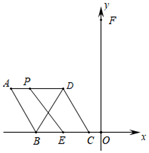 A、 B、 C、 D、4. 如图,在矩形ABCD中,AD= AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC= MP;④BP= AB;⑤点F是△CMP外接圆的圆心.其中正确的个数为( )
A、 B、 C、 D、4. 如图,在矩形ABCD中,AD= AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC= MP;④BP= AB;⑤点F是△CMP外接圆的圆心.其中正确的个数为( )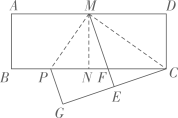 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
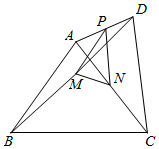
5. 如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .
 6. 如图,在 中, , ,以点A为圆心, 长为半径画弧,交 延长线于点D,过点C作 ,交 于点 ,连接BE,则 的值为.
6. 如图,在 中, , ,以点A为圆心, 长为半径画弧,交 延长线于点D,过点C作 ,交 于点 ,连接BE,则 的值为.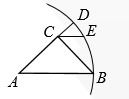 7. 如图,在 中, ,D是 上一点(点D与点A不重合).若在 的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点,则 长的取值范围是.
7. 如图,在 中, ,D是 上一点(点D与点A不重合).若在 的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点,则 长的取值范围是.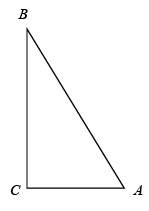 8. 如图,等腰三角形ABC中,AB=AC,BC=6,cos∠ABC= ,点P在边AC上运动(可与点A,C重合),将线段BP绕点P逆时针旋转120°,得到线段DP,连接BD,则BD长的最大值为.
8. 如图,等腰三角形ABC中,AB=AC,BC=6,cos∠ABC= ,点P在边AC上运动(可与点A,C重合),将线段BP绕点P逆时针旋转120°,得到线段DP,连接BD,则BD长的最大值为.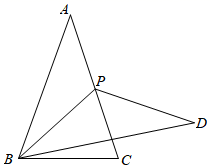 9. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.
9. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.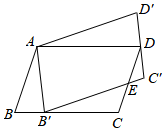 10. 如图, ,在 上截取 .过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;按此规律,所得线段 的长等于.
10. 如图, ,在 上截取 .过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;按此规律,所得线段 的长等于.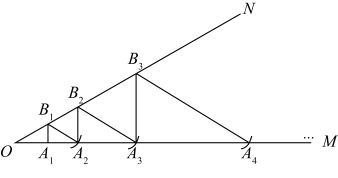 11. 如图,已知点 ,直线 轴,垂足为点 其中 ,若 与 关于直线l对称,且 有两个顶点在函数 的图像上,则k的值为:.
11. 如图,已知点 ,直线 轴,垂足为点 其中 ,若 与 关于直线l对称,且 有两个顶点在函数 的图像上,则k的值为:.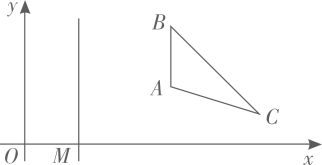 12. 如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为.
12. 如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为.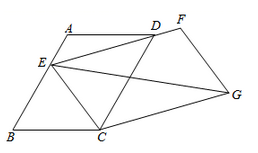 13. 如图,在 中, , ,点D,E分别在边 , 上,且 , 连接 , ,相交于点O,则 面积最大值为.
13. 如图,在 中, , ,点D,E分别在边 , 上,且 , 连接 , ,相交于点O,则 面积最大值为.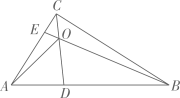 14. 如图,过点C(3,4)的直线 交 轴于点A,∠ABC=90°,AB=CB,曲线 过点B,将点A沿 轴正方向平移 个单位长度恰好落在该曲线上,则 的值为.
14. 如图,过点C(3,4)的直线 交 轴于点A,∠ABC=90°,AB=CB,曲线 过点B,将点A沿 轴正方向平移 个单位长度恰好落在该曲线上,则 的值为.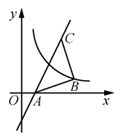 15. 如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则 的最大值是.
15. 如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则 的最大值是.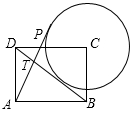
三、综合题
-
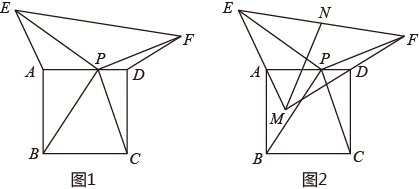
16. 如图1,正方形 的边长为4,点 在边 上( 不与 重合),连接 .将线段 绕点 顺时针旋转90°得到 ,将线段 绕点 逆时针旋转90°得到 .连接 .
 (1)、求证:
(1)、求证:① 的面积 ;
② ;
(2)、如图2, 的延长线交于点 ,取 的中点 ,连接 ,求 的取值范围.17. 如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦CD⊥AB,Q为 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.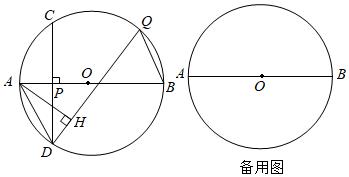 (1)、若m=3.
(1)、若m=3.①求证:∠OAD=60°;
②求 的值;
(2)、用含m的代数式表示 ,请直接写出结果;(3)、存在一个大小确定的⊙O,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值,求此时∠Q的度数.18. 如图,正方形 中,点E在边 上(不与端点A,D重合),点A关于直线 的对称点为点F,连接 ,设 .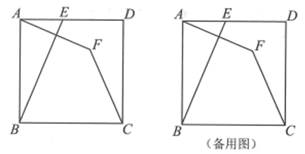 (1)、求 的大小(用含 的式子表示);(2)、过点C作 ,垂足为G,连接 .判断 与 的位置关系,并说明理由;(3)、将 绕点B顺时针旋转 得到 ,点E的对应点为点H,连接 , .当 为等腰三角形时,求 的值.19. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.
(1)、求 的大小(用含 的式子表示);(2)、过点C作 ,垂足为G,连接 .判断 与 的位置关系,并说明理由;(3)、将 绕点B顺时针旋转 得到 ,点E的对应点为点H,连接 , .当 为等腰三角形时,求 的值.19. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.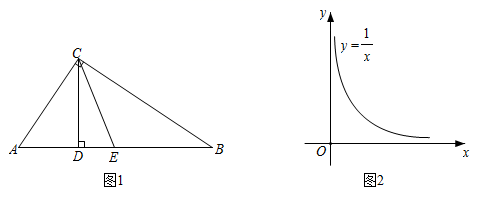 (1)、【理解】
(1)、【理解】
如图1, ,垂足分别为C、D,E是 的中点,连接 .已知 , .①分别求线段 、 的长(用含a、b的代数式表示);
②比较大小: ▲ (填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
(2)、【应用】
如图2,在平面直角坐标系 中,点M、N在反比例函数 的图象上,横坐标分别为m、n.设 ,记 .①当 时, ▲ ;当 时, ▲ ;
②通过归纳猜想,可得l的最小值是 ▲ .请利用图2构造恰当的图形,并说明你的猜想成立.
20. 已知四边形 是边长为1的正方形,点E是射线 上的动点,以 为直角边在直线 的上方作等腰直角三角形 , ,设 . (1)、如图1,若点E在线段 上运动, 交 于点P, 交 于点Q,连结 ,
(1)、如图1,若点E在线段 上运动, 交 于点P, 交 于点Q,连结 ,①当 时,求线段 的长;
②在 中,设边 上的高为h,请用含m的代数式表示h,并求h的最大值;
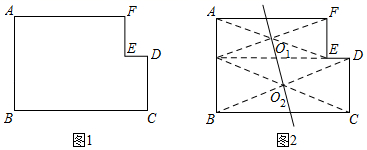
(2)、设过 的中点且垂直于 的直线被等腰直角三角形 截得的线段长为y,请直接写出y与m的关系式.21. 如图1,∠A=∠B=∠C=∠D=∠E=∠F=90°,AB,FE,DC为铅直方向的边,AF,ED,BC为水平方向的边,点E在AB,CD之间,且在AF,BC之间,我们称这样的图形为“L图形”,记作“L图形ABC﹣DEF”.若直线将L图形分成面积相等的两个图形,则称这样的直线为该L图形的面积平分线.(1)、【活动】小华同学给出了图1的面积平分线的一个作图方案:如图2,将这个L图形分成矩形AGEF、矩形GBCD,这两个矩形的对称中心O1 , O2所在直线是该L图形的面积平分线.请用无刻度的直尺在图1中作出其他的面积平分线.(作出一种即可,不写作法,保留作图痕迹)
 (2)、【思考】
(2)、【思考】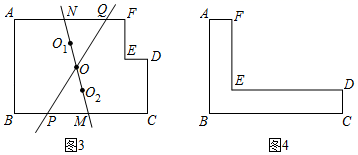
如图3,直线O1O2是小华作的面积平分线,它与边BC,AF分别交于点M,N,过MN的中点O的直线分别交边BC,AF于点P,Q,直线PQ(填“是”或“不是”)L图形ABCDEF的面积平分线.
(3)、【应用】在L图形ABCDEF形中,已知AB=4,BC=6.
如图4,CD=AF=1.
①该L图形的面积平分线与两条水平的边分别相交于点P,Q,求PQ长的最大值;
②该L图形的面积平分线与边AB,CD分别相交于点G,H,当GH的长取最小值时,BG的长为 ▲ .
(4)、设 =t(t>0),在所有的与铅直方向的两条边相交的面积平分线中,如果只有与边AB,CD相交的面积平分线,直接写出t的取值范围.22. 如图1,正方形ABCD的边长为4,点P在边BC上,⊙O经过A,B,P三点.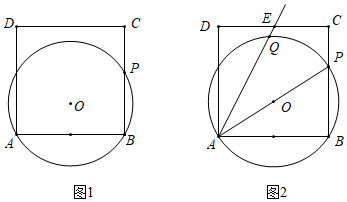 (1)、若BP=3,判断边CD所在直线与⊙O的位置关系,并说明理由;(2)、如图2,E是CD的中点,⊙O交射线AE于点Q,当AP平分∠EAB时,求tan∠EAP的值.23. (知识再现)
(1)、若BP=3,判断边CD所在直线与⊙O的位置关系,并说明理由;(2)、如图2,E是CD的中点,⊙O交射线AE于点Q,当AP平分∠EAB时,求tan∠EAP的值.23. (知识再现)学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称HL定理)”是判定直角三角形全等的特有方法.
 (1)、(简单应用)
(1)、(简单应用)如图(1),在△ABC中,∠BAC=90°,AB=AC,点D、E分别在边AC、AB上.若CE=BD,则线段AE和线段AD的数量关系是.
(2)、(拓展延伸)在△ABC中,∠BAC= (90°< <180°),AB=AC=m,点D在边AC上.
若点E在边AB上,且CE=BD,如图(2)所示,则线段AE与线段AD相等吗?如果相等,请给出证明;如果不相等,请说明理由.
(3)、若点E在BA的延长线上,且CE=BD.试探究线段AE与线段AD的数量关系(用含有a、m的式子表示),并说明理由.24. 已知正方形ABCD与正方形AEFG,正方形AEFG绕点A旋转一周. (1)、如图①,连接BG、CF,求 的值;(2)、当正方形AEFG旋转至图②位置时,连接CF、BE,分别去CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)、连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.25. 在几何体表面上,蚂蚁怎样爬行路径最短?
(1)、如图①,连接BG、CF,求 的值;(2)、当正方形AEFG旋转至图②位置时,连接CF、BE,分别去CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)、连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.25. 在几何体表面上,蚂蚁怎样爬行路径最短?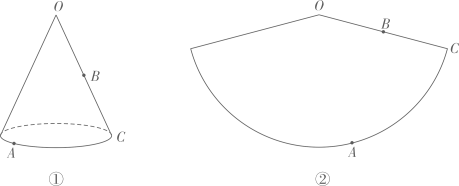
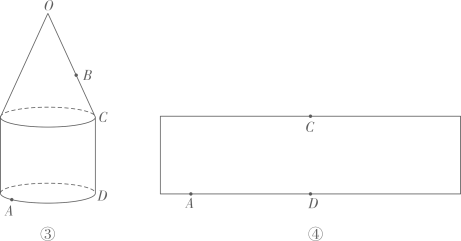 (1)、如图①,圆锥的母线长为 ,B为母线 的中点,点A在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).(2)、图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.
(1)、如图①,圆锥的母线长为 ,B为母线 的中点,点A在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).(2)、图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.①蚂蚁从点A爬行到点O的最短路径的长为 ▲ (用含l,h的代数式表示).
②设 的长为a,点B在母线 上, .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
26. 如图,在矩形 中,线段 、 分别平行于 、 ,它们相交于点 ,点 、 分别在线段 、 上, , ,连接 、 , 与 交于点 .已知 .设 , .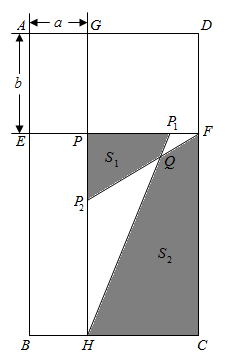 (1)、四边形 的面积四边形 的面积(填“ ”、“ ”或“ ”);(2)、求证: ;(3)、设四边形 的面积为 ,四边形 的面积为 ,求 的值.27. 在一次数学探究活动中,李老师设计了一份活动单:
(1)、四边形 的面积四边形 的面积(填“ ”、“ ”或“ ”);(2)、求证: ;(3)、设四边形 的面积为 ,四边形 的面积为 ,求 的值.27. 在一次数学探究活动中,李老师设计了一份活动单:已知线段 ,使用作图工具作 ,尝试操作后思考:
( 1 )这样的点A唯一吗?
( 2 )点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以 为弦的圆弧上(点B、C除外),…….小华同学画出了符合要求的一条圆弧(如图1).
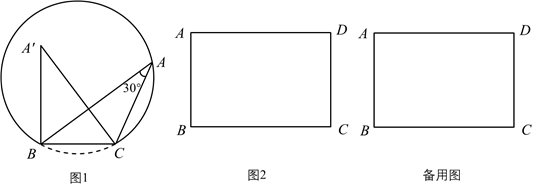 (1)、小华同学提出了下列问题,请你帮助解决.
(1)、小华同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为;
② 面积的最大值为;
(2)、经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为 ,请你利用图1证明 ;(3)、请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , ,点P在直线 的左侧,且 .①线段 长的最小值为;
②若 ,则线段 长为.
28. 在数学兴趣小组活动中,小亮进行数学探究活动.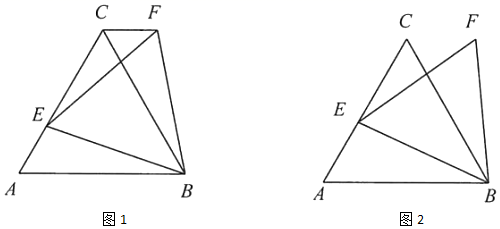
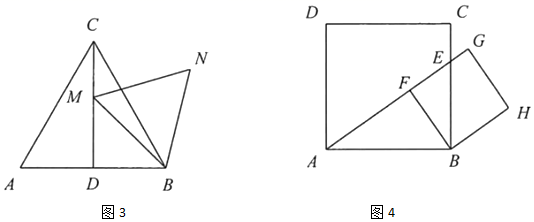 (1)、 是边长为3的等边三角形,E是边 上的一点,且 ,小亮以 为边作等边三角形 ,如图1,求 的长;(2)、 是边长为3的等边三角形,E是边 上的一个动点,小亮以 为边作等边三角形 ,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;(3)、 是边长为3的等边三角形,M是高 上的一个动点,小亮以 为边作等边三角形 ,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;(4)、正方形 的边长为3,E是边 上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形 ,其中点F、G都在直线 上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为 , 点G所经过的路径长为.29. 我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分割点.它们的比值为 .
(1)、 是边长为3的等边三角形,E是边 上的一点,且 ,小亮以 为边作等边三角形 ,如图1,求 的长;(2)、 是边长为3的等边三角形,E是边 上的一个动点,小亮以 为边作等边三角形 ,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;(3)、 是边长为3的等边三角形,M是高 上的一个动点,小亮以 为边作等边三角形 ,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;(4)、正方形 的边长为3,E是边 上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形 ,其中点F、G都在直线 上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为 , 点G所经过的路径长为.29. 我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分割点.它们的比值为 . (1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.30. 如图,正方形 的边长为6, 为 的中点, 为等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,连接 .
(1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.30. 如图,正方形 的边长为6, 为 的中点, 为等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,连接 .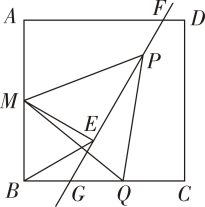 (1)、求证: .(2)、当点 在线段 上时,试判断 的值是否变化?如果不变,求出这个值,如果变化,请说明理由.(3)、设 ,点 关于 的对称点为 ,若点 落在 的内部,试写出 的范围,并说明理由.31. 如图
(1)、求证: .(2)、当点 在线段 上时,试判断 的值是否变化?如果不变,求出这个值,如果变化,请说明理由.(3)、设 ,点 关于 的对称点为 ,若点 落在 的内部,试写出 的范围,并说明理由.31. 如图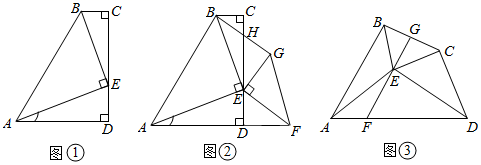 (1)、(感知)如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证: = .(2)、(探究)如图②,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD上,点F在边AD的延长线上,∠FEG=∠AEB=90°,且 = ,连接BG交CD于点H.求证:BH=GH.(3)、(拓展)如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且 = ,过E作EF交AD于点F,若∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.32. (了解概念)
(1)、(感知)如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证: = .(2)、(探究)如图②,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD上,点F在边AD的延长线上,∠FEG=∠AEB=90°,且 = ,连接BG交CD于点H.求证:BH=GH.(3)、(拓展)如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且 = ,过E作EF交AD于点F,若∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.32. (了解概念)有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.
 (1)、(理解运用)
(1)、(理解运用)如图①,对余四边形ABCD中,AB=5,BC=6,CD=4,连接AC.若AC=AB,求sin∠CAD的值;
(2)、如图②,凸四边形ABCD中,AD=BD,AD⊥BD,当2CD2+CB2=CA2时,判断四边形ABCD是否为对余四边形.证明你的结论;(3)、(拓展提升)在平面直角坐标系中,点A(﹣1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC=90°+∠ABC.设 =u,点D的纵坐标为t,请直接写出u关于t的函数解析式.
33. 矩形ABCD中,AB=8,AD=12.将矩形折叠,使点A落在点P处,折痕为DE.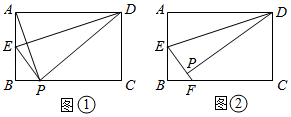 (1)、如图①,若点P恰好在边BC上,连接AP,求 的值;(2)、如图②,若E是AB的中点,EP的延长线交BC于点F,求BF的长.34. 如图1,已知点O在四边形ABCD的边AB上,且 ,OC平分 ,与BD交于点G,AC分别与BD、OD交于点E、F.
(1)、如图①,若点P恰好在边BC上,连接AP,求 的值;(2)、如图②,若E是AB的中点,EP的延长线交BC于点F,求BF的长.34. 如图1,已知点O在四边形ABCD的边AB上,且 ,OC平分 ,与BD交于点G,AC分别与BD、OD交于点E、F.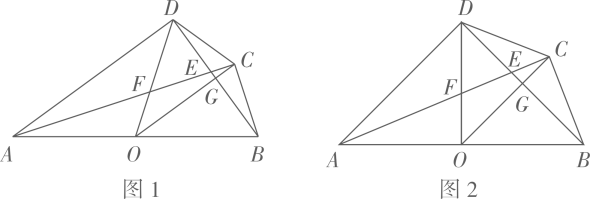 (1)、求证: ;(2)、如图2,若 ,求 的值;(3)、当四边形ABCD的周长取最大值时,求 的值.35. 如图,在矩形 中, , ,点E为边 上的一点(与C、D不重合)四边形 关于直线 的对称图形为四边形 ,延长 交 与点P,记四边形 的面积为S.
(1)、求证: ;(2)、如图2,若 ,求 的值;(3)、当四边形ABCD的周长取最大值时,求 的值.35. 如图,在矩形 中, , ,点E为边 上的一点(与C、D不重合)四边形 关于直线 的对称图形为四边形 ,延长 交 与点P,记四边形 的面积为S.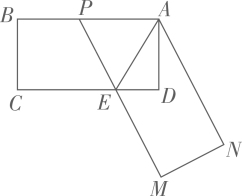 (1)、若 ,求S的值;(2)、设 ,求S关于x的函数表达式.36. 如图,已知 , 是 的平分线,A是射线 上一点, .动点P从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点Q从点O出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点B.经过O、P、Q三点作圆,交 于点C,连接 、 .设运动时间为 ,其中 .
(1)、若 ,求S的值;(2)、设 ,求S关于x的函数表达式.36. 如图,已知 , 是 的平分线,A是射线 上一点, .动点P从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点Q从点O出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点B.经过O、P、Q三点作圆,交 于点C,连接 、 .设运动时间为 ,其中 .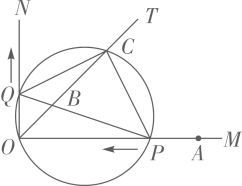 (1)、求 的值;(2)、是否存在实数t,使得线段 的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、求四边形 的面积.37. 如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短.
(1)、求 的值;(2)、是否存在实数t,使得线段 的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、求四边形 的面积.37. 如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短. (1)、如图②,作出点A关于l的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点 ,连接 , , 证明 , 请完成这个证明.
(1)、如图②,作出点A关于l的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点 ,连接 , , 证明 , 请完成这个证明.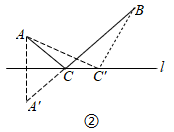 (2)、如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由),
(2)、如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由),①生市保护区是正方形区城,位置如图③所示
②生态保护区是圆形区域,位置如图④所示.
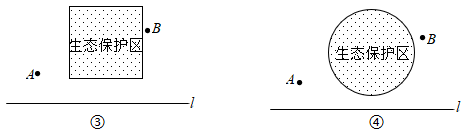 38.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;
38.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;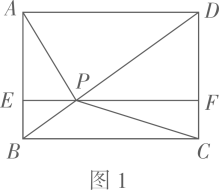 (2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
(2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);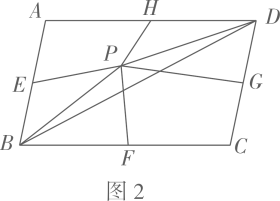 (3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
(3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);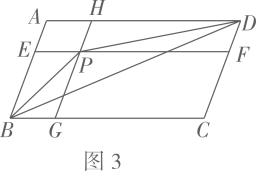 (4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).
(4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).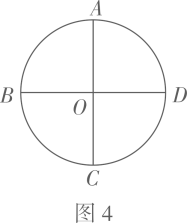 39.(1)、(初步尝试)
39.(1)、(初步尝试)如图①,在三角形纸片 中, ,将 折叠,使点B与点C重合,折痕为 ,则 与 的数量关系为;
 (2)、(思考说理)
(2)、(思考说理)如图②,在三角形纸片 中, , ,将 折叠,使点B与点C重合,折痕为 ,求 的值.
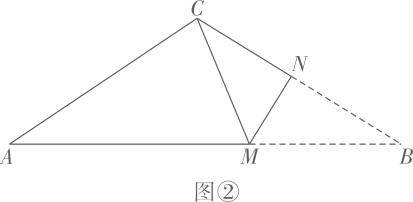 (3)、如图③,在三角形纸片 中, , , ,将 沿过顶点 的直线折叠,使点B落在边 上的点 处,折痕为 .
(3)、如图③,在三角形纸片 中, , , ,将 沿过顶点 的直线折叠,使点B落在边 上的点 处,折痕为 .①求线段 的长;
②若点O是边 的中点,点P为线段 上的一个动点,将 沿 折叠得到 ,点A的对应点为点 , 与 交于点F,求 的取值范围.
 40. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.
40. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.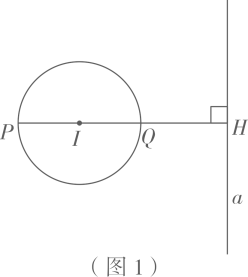
 (1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.
(1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_▲__(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_▲__;
②若直线n的函数表达式为 ,求 关于直线n的“特征数”;
(2)、在平面直角坐标系 中,直线l经过点 ,点F是坐标平面内一点,以F为圆心, 为半径作⊙F.若⊙F与直线l相离,点 是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是 ,求直线l的函数表达式.41. 已知平面图形 ,点 、 是 上任意两点,我们把线段 的长度的最大值称为平面图形 的“宽距”.例如,正方形的宽距等于它的对角线的长度.(1)、写出下列图形的宽距:①半径为 的圆:;
②如图,上方是半径为 的半圆,下方是正方形的三条边的“窗户形“:;
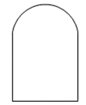 (2)、如图,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .
(2)、如图,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .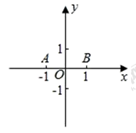
①若 ,用直尺和圆规画出点 所在的区域并求它的面积(所在区域用阴影表示);
②若点 在⊙ 上运动,⊙ 的半径为 ,圆心 在过点 且与 轴垂直的直线上.对于⊙ 上任意点 ,都有 ,直接写出圆心 的横坐标 的取值范围.
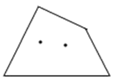
42. 【阅读】数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.(1)、【理解】如图,两个边长分别为 、 、 的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
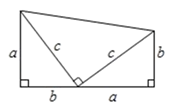 (2)、如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(2)、如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ; (3)、【运用】
(3)、【运用】边形有 个顶点,在它的内部再画 个点,以( )个点为顶点,把 边形剪成若干个三角形,设最多可以剪得 个这样的三角形.当 , 时,如图,最多可以剪得 个这样的三角形,所以 .
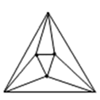
①当 , 时,如图, ;当 , 时, ;
②对于一般的情形,在 边形内画 个点,通过归纳猜想,可得 (用含 、 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
43. 如图①,在钝角 中, , ,点 为边 中点,点 为边 中点,将 绕点 逆时针方向旋转 度( ).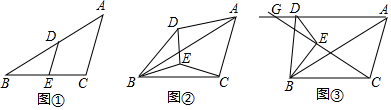 (1)、如图②,当 时,连接 、 .求证: ;(2)、如图③,直线 、 交于点 .在旋转过程中, 的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)、将 从图①位置绕点 逆时针方向旋转 ,求点 的运动路程.44. 如图,已知等边△ABC的边长为8,点P事AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
(1)、如图②,当 时,连接 、 .求证: ;(2)、如图③,直线 、 交于点 .在旋转过程中, 的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)、将 从图①位置绕点 逆时针方向旋转 ,求点 的运动路程.44. 如图,已知等边△ABC的边长为8,点P事AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.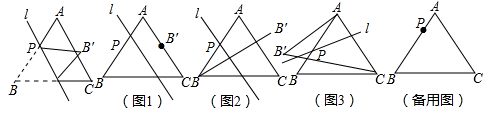 (1)、如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为;(2)、如图2,当PB=5时,若直线l∥AC,则BB’的长度为;(3)、如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)、当PB=6时,在直线l变化过程中,求△ACB’面积的最大值。45. 如图1,在矩形 中,BC=3,动点 从 出发,以每秒1个单位的速度,沿射线 方向移动,作 关于直线 的对称 ,设点 的运动时间为
(1)、如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为;(2)、如图2,当PB=5时,若直线l∥AC,则BB’的长度为;(3)、如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)、当PB=6时,在直线l变化过程中,求△ACB’面积的最大值。45. 如图1,在矩形 中,BC=3,动点 从 出发,以每秒1个单位的速度,沿射线 方向移动,作 关于直线 的对称 ,设点 的运动时间为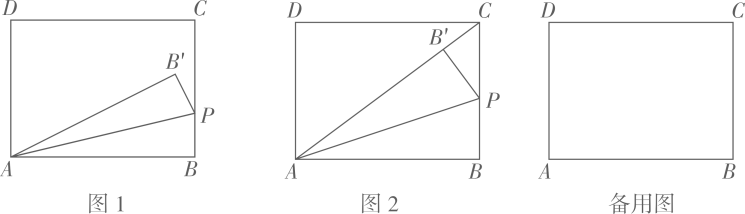 (1)、若
(1)、若①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)、当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.