江苏中考数学历年真题分类卷13 三角形的性质及变换
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 将一副三角板按如图方式重叠,则 的度数为( )
 A、 B、 C、 D、2. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、2. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )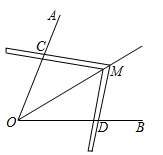 A、 B、 C、 D、3. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A、 B、 C、 D、3. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )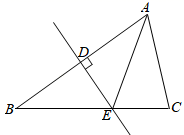 A、2 B、4 C、6 D、84. 如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
A、2 B、4 C、6 D、84. 如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )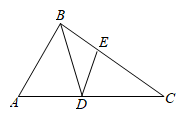 A、30° B、40° C、50° D、60°5. 下列长度的三条线段与长度为5的线段能组成四边形的是( )A、1,1,1 B、1,1,8 C、1,2,2 D、2,2,26. 如图,点A、B、C、D、E在同一平面内,连接 、 、 、 、 ,若 ,则 ( )
A、30° B、40° C、50° D、60°5. 下列长度的三条线段与长度为5的线段能组成四边形的是( )A、1,1,1 B、1,1,8 C、1,2,2 D、2,2,26. 如图,点A、B、C、D、E在同一平面内,连接 、 、 、 、 ,若 ,则 ( )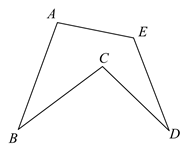 A、 B、 C、 D、7. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、 B、 C、 D、7. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、58. 如图, 中, , 、 相交于点D, , , ,则 的面积是( )
A、2 B、3 C、4 D、58. 如图, 中, , 、 相交于点D, , , ,则 的面积是( )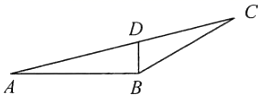 A、 B、 C、 D、9. 在△ABC中,AB=1,BC= ,下列选项中,可以作为AC长度的是( )A、2 B、4 C、5 D、610. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )
A、 B、 C、 D、9. 在△ABC中,AB=1,BC= ,下列选项中,可以作为AC长度的是( )A、2 B、4 C、5 D、610. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )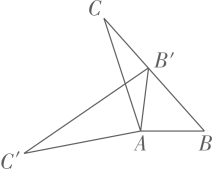 A、 B、 C、 D、11. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )
A、 B、 C、 D、11. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )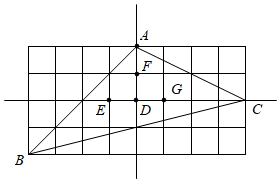 A、点 B、点 C、点 D、点12. 下列长度的3根小木棒不能搭成三角形的是( )A、2cm,3cm,4cm B、1cm,2cm,3cm C、3cm,4cm,5cm D、4cm,5cm,6cm13. 下列长度的三条线段,能组成三角形的是( )A、 , , B、 , ,12 C、 , , D、 , ,14. 一副三角板如图摆放(直角顶点 重合),边 与 交于点 , ,则 等于( )
A、点 B、点 C、点 D、点12. 下列长度的3根小木棒不能搭成三角形的是( )A、2cm,3cm,4cm B、1cm,2cm,3cm C、3cm,4cm,5cm D、4cm,5cm,6cm13. 下列长度的三条线段,能组成三角形的是( )A、 , , B、 , ,12 C、 , , D、 , ,14. 一副三角板如图摆放(直角顶点 重合),边 与 交于点 , ,则 等于( )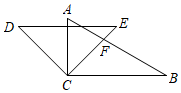 A、 B、 C、 D、15. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( )
A、 B、 C、 D、15. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( ) A、①处 B、②处 C、③处 D、④处16. 已知n正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有( )A、4个 B、5个 C、6个 D、7个
A、①处 B、②处 C、③处 D、④处16. 已知n正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有( )A、4个 B、5个 C、6个 D、7个二、填空题
-
17. 如图,在 中,点D、E分别在 、 上, .若 ,则 .
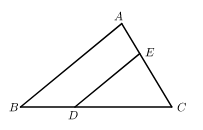 18. 如图,在 中, ,点D、E分别在 、 上,点F在 内.若四边形 是边长为1的正方形,则 .
18. 如图,在 中, ,点D、E分别在 、 上,点F在 内.若四边形 是边长为1的正方形,则 . 19. 如图,点A,B,C,O在网格中小正方形的顶点处,直线l经过点C,O,将 ABC沿l平移得到 MNO,M是A的对应点,再将这两个三角形沿l翻折,P,Q分别是A,M的对应点.已知网格中每个小正方形的边长都等于1,则PQ的长为.
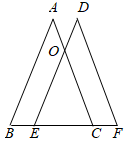
19. 如图,点A,B,C,O在网格中小正方形的顶点处,直线l经过点C,O,将 ABC沿l平移得到 MNO,M是A的对应点,再将这两个三角形沿l翻折,P,Q分别是A,M的对应点.已知网格中每个小正方形的边长都等于1,则PQ的长为.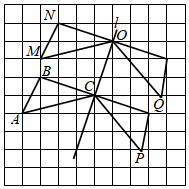 20. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.
20. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.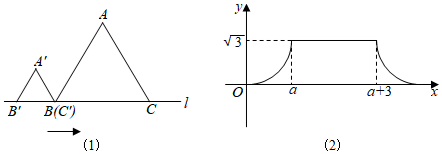 21. 一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是.22. 《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为尺.
21. 一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是.22. 《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为尺. 23. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).
23. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).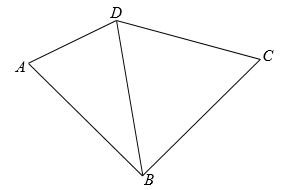 24. 如图.在 中, , .若 ,则 .
24. 如图.在 中, , .若 ,则 .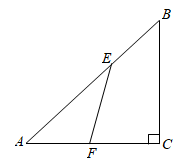 25. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.
25. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.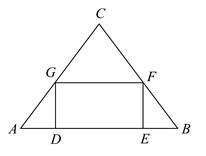 26. 如图,在 中, ,点D是 的中点,过点D作 ,垂足为点E,连接 ,若 , ,则 .
26. 如图,在 中, ,点D是 的中点,过点D作 ,垂足为点E,连接 ,若 , ,则 .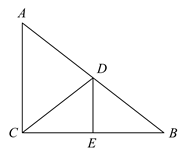 27. 如图, 是 的中线,点F在 上,延长 交 于点D.若 ,则 .
27. 如图, 是 的中线,点F在 上,延长 交 于点D.若 ,则 .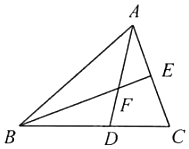 28. 在 中,若 , ,则 的面积的最大值为.29. 如图,在△ABC中,BC=3,将△ABC平移5个单位长度得到△A1B1C1 , 点P、Q分别是AB、A1C1的中点,PQ的最小值等于.
28. 在 中,若 , ,则 的面积的最大值为.29. 如图,在△ABC中,BC=3,将△ABC平移5个单位长度得到△A1B1C1 , 点P、Q分别是AB、A1C1的中点,PQ的最小值等于. 30. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为.
30. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为. 31. 如图所示的网格由边长为 个单位长度的小正方形组成,点 、 、 、在直角坐标系中的坐标分别为 , , ,则 内心的坐标为.
31. 如图所示的网格由边长为 个单位长度的小正方形组成,点 、 、 、在直角坐标系中的坐标分别为 , , ,则 内心的坐标为. 32. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为.
32. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为. 33. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于.
33. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于. 34. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高.
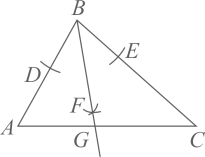
34. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高. 35. 如图,在 中,按以下步骤作图:
35. 如图,在 中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交AB、BC于点D、E.
②分别以点D、E为圆心,大于 的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果 , , 的面积为18,则 的面积为.
 36. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 =.
36. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 =.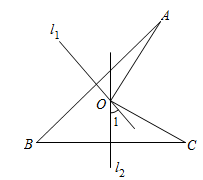 37. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °.
37. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °. 38. 如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为.
38. 如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为.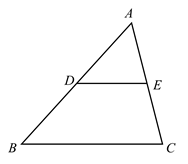 39. 直线 与x轴,y轴分别交于A,B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有.40. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°
39. 直线 与x轴,y轴分别交于A,B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有.40. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°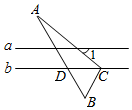 41. 如图, ,若 的顶点 在射线 上,且 ,点 在射线 上运动,当 是锐角三角形时, 的取值范围是.
41. 如图, ,若 的顶点 在射线 上,且 ,点 在射线 上运动,当 是锐角三角形时, 的取值范围是. 42. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.
42. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.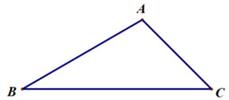 43. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为.
43. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为.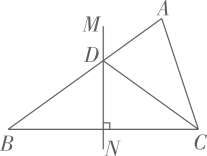 44. 在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是.
44. 在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是.三、作图题
-
45. 如图, 中, , , .
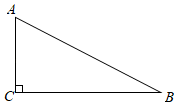 (1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.
(1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.四、解答题
-
46. 如图,三条笔直公路两两相交,交点分别为A、B、C,测得 , , 千米,求A、B两点间的距离.(参考数据: , ,结果精确到1千米).
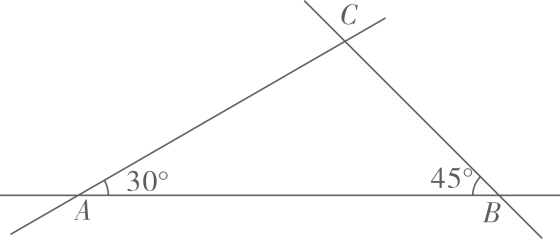 47. 如图,有一池塘 要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C , 连接AC并延长到D , 使 连接BC并延长到E , 使 连接DE , 那么量出DE的长,就是A、B的距离 请说明DE的长就是A、B的距离的理由.
47. 如图,有一池塘 要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C , 连接AC并延长到D , 使 连接BC并延长到E , 使 连接DE , 那么量出DE的长,就是A、B的距离 请说明DE的长就是A、B的距离的理由.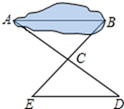
五、综合题
-
48. 如图,B、F、C、E是直线l上的四点, .
 (1)、求证: ;(2)、将 沿直线l翻折得到 .
(1)、求证: ;(2)、将 沿直线l翻折得到 .①用直尺和圆规在图中作出 (保留作图痕迹,不要求写作法);
②连接 ,则直线 与l的位置关系是▲ .
49. 如图,已知锐角 中, .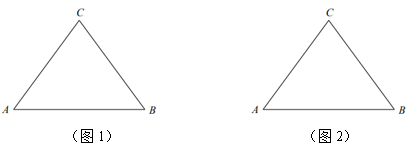 (1)、请在图1中用无刻度的直尺和圆规作图:作 的平分线 ;作 的外接圆 ;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , 的半径为5,则 .(如需画草图,请使用图2)50. 已知:如图, , 相交于点O, , .
(1)、请在图1中用无刻度的直尺和圆规作图:作 的平分线 ;作 的外接圆 ;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , 的半径为5,则 .(如需画草图,请使用图2)50. 已知:如图, , 相交于点O, , .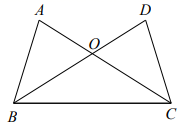
求证:
(1)、 ;(2)、 .51. 如图,方格纸上每个小正方形的边长均为1个单位长度,△ABC的顶点A、B、C都在格点上(两条网格线的交点叫格点).请仅用无刻度的直尺按下列要求画图,并保留画图痕迹(不要求写画法).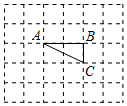 (1)、将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B1,点C的对应点为C1 , 画出△AB1C1;(2)、连接CC1 , △ACC1的面积为;(3)、在线段CC1上画一点D,使得△ACD的面积是△ACC1面积的 .52. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.
(1)、将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B1,点C的对应点为C1 , 画出△AB1C1;(2)、连接CC1 , △ACC1的面积为;(3)、在线段CC1上画一点D,使得△ACD的面积是△ACC1面积的 .52. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.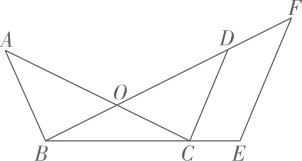 (1)、求证 ;(2)、若 ,求 的长.53. 如图, , , . , 与 交于点 .
(1)、求证 ;(2)、若 ,求 的长.53. 如图, , , . , 与 交于点 .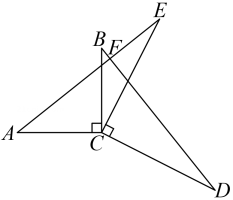 (1)、求证: ;(2)、求 的度数.54. 如图,已知 , , .
(1)、求证: ;(2)、求 的度数.54. 如图,已知 , , .

求证:
(1)、 ;(2)、 .55. 问题1:如图①,在四边形 中, , 是 上一点, , .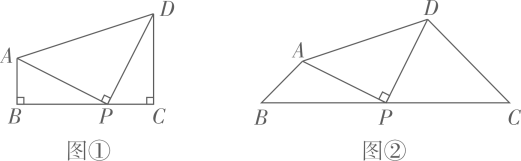 (1)、求证: .(2)、如图②,在四边形 中, , 是 上一点, , .求 的值.56. 已知:如图,点A、B、C、D在一条直线上, .
(1)、求证: .(2)、如图②,在四边形 中, , 是 上一点, , .求 的值.56. 已知:如图,点A、B、C、D在一条直线上, .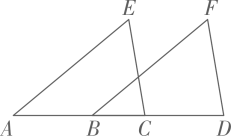 (1)、求证: ;(2)、若 ,求 的度数.57. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
(1)、求证: ;(2)、若 ,求 的度数.57. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
 (1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.
(1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.①请你在图1中用直尺和圆规画出线段 经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法)该图形的面积为;
②如图2,在旋转过程中,线段 与 交于点O,当 时,求 的长.
-