江苏中考数学历年真题分类卷14 四边形和多边形的性质及变换
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
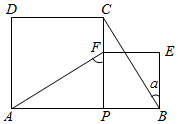
1. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
 A、2α B、90°﹣α C、45°+α D、90°﹣ α2. 如图,D、E、F分别是 各边中点,则以下说法错误的是( )
A、2α B、90°﹣α C、45°+α D、90°﹣ α2. 如图,D、E、F分别是 各边中点,则以下说法错误的是( ) A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形3. 折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )A、 B、2 C、 D、44. 如图,在平行四边形 中,将 沿着 所在的直线翻折得到 , 交 于点 ,连接 ,若 , , ,则 的长是( )
A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形3. 折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )A、 B、2 C、 D、44. 如图,在平行四边形 中,将 沿着 所在的直线翻折得到 , 交 于点 ,连接 ,若 , , ,则 的长是( )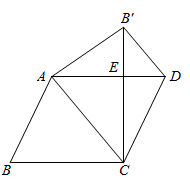 A、1 B、 C、 D、5. 如图,将矩形纸片 沿 折叠后,点D、C分别落在点 、 的位置, 的延长线交 于点G,若 ,则 等于( )
A、1 B、 C、 D、5. 如图,将矩形纸片 沿 折叠后,点D、C分别落在点 、 的位置, 的延长线交 于点G,若 ,则 等于( )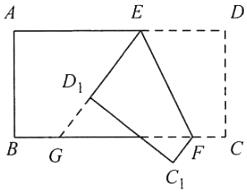 A、 B、 C、 D、6. 正五边形的内角和是( )A、 B、 C、 D、7. 正十边形的每一个外角的度数为( )A、 B、 C、 D、8. 下列条件中,能判定▱ABCD是菱形的是( )A、AC=BD B、AB⊥BC C、AD=BD D、AC⊥BD9. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( )
A、 B、 C、 D、6. 正五边形的内角和是( )A、 B、 C、 D、7. 正十边形的每一个外角的度数为( )A、 B、 C、 D、8. 下列条件中,能判定▱ABCD是菱形的是( )A、AC=BD B、AB⊥BC C、AD=BD D、AC⊥BD9. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( ) A、 B、 C、3 D、510. 如图,小明从点A出发沿直线前进10米到达点B,向左转 后又沿直线前进10米到达点C,再向左转 后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
A、 B、 C、3 D、510. 如图,小明从点A出发沿直线前进10米到达点B,向左转 后又沿直线前进10米到达点C,再向左转 后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
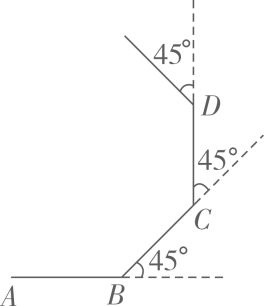 A、100米 B、80米 C、60米 D、40米11. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )
A、100米 B、80米 C、60米 D、40米11. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )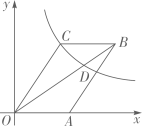 A、 B、 C、 D、12. 如图,将矩形纸片 沿 折叠,使点A落在对角线 上的 处.若 ,则 等于( ).
A、 B、 C、 D、12. 如图,将矩形纸片 沿 折叠,使点A落在对角线 上的 处.若 ,则 等于( ).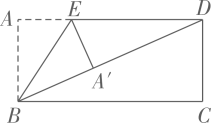 A、 B、 C、 D、13. 如图,点D是 内一点, 与x轴平行, 与y轴平行, .若反比例函数 的图像经过A、D两点,则k的值是( )
A、 B、 C、 D、13. 如图,点D是 内一点, 与x轴平行, 与y轴平行, .若反比例函数 的图像经过A、D两点,则k的值是( )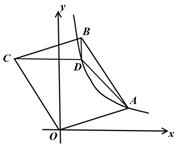 A、 B、4 C、 D、614. 如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为( )
A、 B、4 C、 D、614. 如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为( )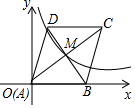 A、 B、 C、2 D、15. 下列结论中,矩形具有而菱形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直
A、 B、 C、2 D、15. 下列结论中,矩形具有而菱形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直二、填空题
-
16. 如图,四边形 与 均为矩形,点 分别在线段 上.若 ,矩形 的周长为 ,则图中阴影部分的面积为 .
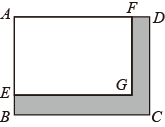 17. 如图,在平面直角坐标系 中,四边形 是平行四边形,其中点A在x轴正半轴上.若 ,则点A的坐标是.
17. 如图,在平面直角坐标系 中,四边形 是平行四边形,其中点A在x轴正半轴上.若 ,则点A的坐标是.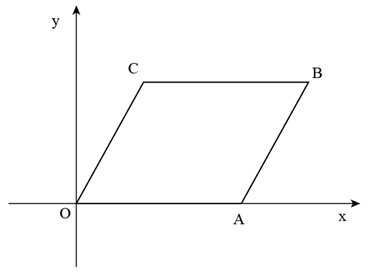 18. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图所示,在 中,分别取 、 的中点D、E,连接 ,过点A作 ,垂足为F,将 分割后拼接成矩形 .若 ,则 的面积是.
18. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图所示,在 中,分别取 、 的中点D、E,连接 ,过点A作 ,垂足为F,将 分割后拼接成矩形 .若 ,则 的面积是. 19. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.
19. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.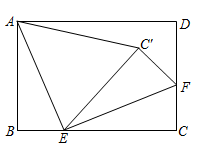 20. 如图,在平面直角坐标系中, 的边 的中点C,D的横坐标分别是1,4,则点B的横坐标是.
20. 如图,在平面直角坐标系中, 的边 的中点C,D的横坐标分别是1,4,则点B的横坐标是.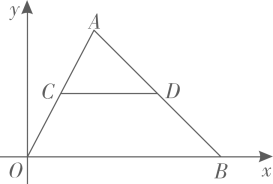 21. 如图,在 中,点E在 上,且 平分 ,若 , ,则 的面积为.
21. 如图,在 中,点E在 上,且 平分 ,若 , ,则 的面积为.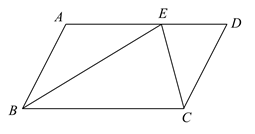 22. 如图,菱形 的对角线 、 相交于点O, ,垂足为E, , ,则 的长为.
22. 如图,菱形 的对角线 、 相交于点O, ,垂足为E, , ,则 的长为. 23. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .
23. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .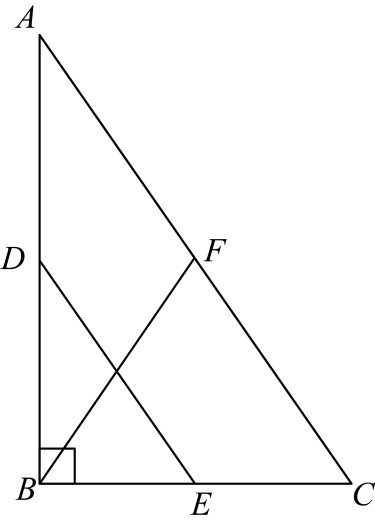 24. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
24. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.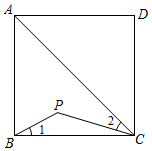 25. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为.
25. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为. 26. 如图,在菱形 中, ,点E在 上,若 ,则 .
26. 如图,在菱形 中, ,点E在 上,若 ,则 .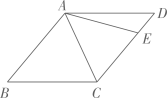 27. 如图,已知 是一个锐角,以点O为圆心,任意长为半径画弧,分别交 、 于点A、B,再分别以点A、B为圆心,大于 长为半径画弧,两弧交于点C,画射线 .过点 作 ,交射线 于点D,过点D作 ,交 于点E.设 , ,则 .
27. 如图,已知 是一个锐角,以点O为圆心,任意长为半径画弧,分别交 、 于点A、B,再分别以点A、B为圆心,大于 长为半径画弧,两弧交于点C,画射线 .过点 作 ,交射线 于点D,过点D作 ,交 于点E.设 , ,则 . 28. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, .如图,建立平面直角坐标系 ,使得边 在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.
28. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, .如图,建立平面直角坐标系 ,使得边 在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.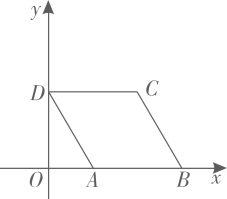 29. 八边形的内角和为度.30. 如图,在矩形ABCD中, , ,H是AB的中点,将 沿CH折叠,点B落在矩形内点P处,连接AP,则 .
29. 八边形的内角和为度.30. 如图,在矩形ABCD中, , ,H是AB的中点,将 沿CH折叠,点B落在矩形内点P处,连接AP,则 . 31. 若一个多边形的内角和是 ,则该多边形的边数是.32. 如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .
31. 若一个多边形的内角和是 ,则该多边形的边数是.32. 如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .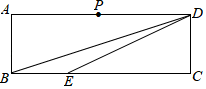 33. 如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于.
33. 如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于.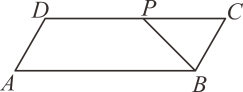 34. 如图,矩形 中, 、 交于点 , 、 分别为 、 的中点.若 ,则 的长为.
34. 如图,矩形 中, 、 交于点 , 、 分别为 、 的中点.若 ,则 的长为. 35. 将边长为 的正方形 绕点 按顺时针方向旋转到 的位置(如图),使得点 落在对角线 上, 与 相交于点 ,则 =.(结果保留根号)
35. 将边长为 的正方形 绕点 按顺时针方向旋转到 的位置(如图),使得点 落在对角线 上, 与 相交于点 ,则 =.(结果保留根号)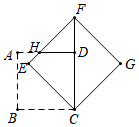 36. 如图,正方形 的边长为4, 为 上一点,且 , 为 边上的一个动点,连接 ,以 为边向右侧作等边 ,连接 ,则 的最小值为.
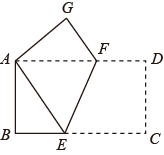
36. 如图,正方形 的边长为4, 为 上一点,且 , 为 边上的一个动点,连接 ,以 为边向右侧作等边 ,连接 ,则 的最小值为.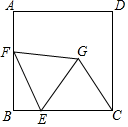 37. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=.
37. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=.
三、作图题
-
38. 如图,点O是正方形, 的中心.
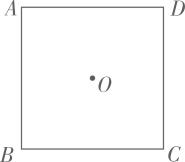 (1)、用直尺和圆规在正方形内部作一点E(异于点O),使得 (保留作图痕迹,不写作法)(2)、连接 求证: .39. 如图,AD是△ABC的角平分线
(1)、用直尺和圆规在正方形内部作一点E(异于点O),使得 (保留作图痕迹,不写作法)(2)、连接 求证: .39. 如图,AD是△ABC的角平分线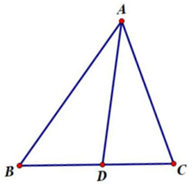 (1)、作线段AD的垂直平分线EF,分别交AB、AC于点E、F;
(1)、作线段AD的垂直平分线EF,分别交AB、AC于点E、F;(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)
(2)、连接DE、DF,四边形AEDF是形.(直接写出答案)40. 按要求作图,不要求写作法,但要保留作图痕迹.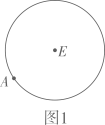
 (1)、如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;(2)、我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
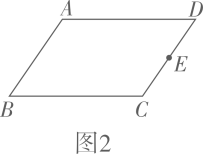
(1)、如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;(2)、我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:①如图2,在▱ABCD中,E为CD的中点,作BC的中点F;
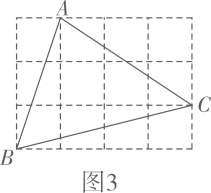
②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH
四、解答题
-
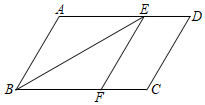
41. 已知:如图,在▱ABCD中,点E、F分别在AD、BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
 42. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
42. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.(注:如果选择多个条件分别解答,按第一个解答计分.)
43. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.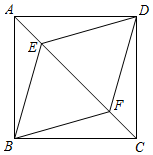 44. 已知:如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.
44. 已知:如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.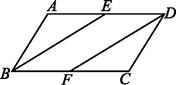
五、综合题
-
45. 如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .
 (1)、求证: 是等腰三角形;(2)、求线段 的长.46. 如图, 、 、 分别是 各边的中点,连接 、 、 .
(1)、求证: 是等腰三角形;(2)、求线段 的长.46. 如图, 、 、 分别是 各边的中点,连接 、 、 .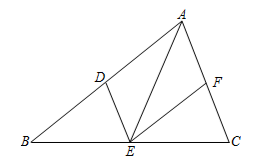 (1)、求证:四边形 为平行四边形;(2)、加上条件 ▲ 后,能使得四边形 为菱形,请从① ;② 平分 ;③ ,这三个条件中选择条件填空(写序号),并加以证明.47. 如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)、求证:四边形 为平行四边形;(2)、加上条件 ▲ 后,能使得四边形 为菱形,请从① ;② 平分 ;③ ,这三个条件中选择条件填空(写序号),并加以证明.47. 如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.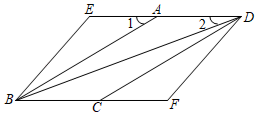 (1)、求证: ;(2)、连接BD,∠1=30°,∠2=20°,当∠ABE=°时,四边形BFDE是菱形.48. 如图,在 中, 的角平分线交 于点D, .
(1)、求证: ;(2)、连接BD,∠1=30°,∠2=20°,当∠ABE=°时,四边形BFDE是菱形.48. 如图,在 中, 的角平分线交 于点D, .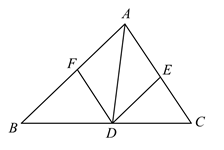 (1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.49. 如图,点C是 的中点,四边形 是平行四边形.
(1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.49. 如图,点C是 的中点,四边形 是平行四边形.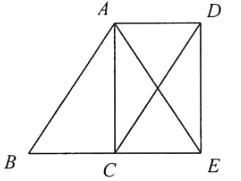 (1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.50. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE.
(1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.50. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE. (1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.51. 如图,在矩形 中,E是 的中点, ,垂足为F.
(1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.51. 如图,在矩形 中,E是 的中点, ,垂足为F.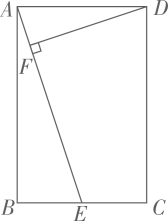 (1)、求证: ;(2)、若 , ,求 的长.52. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于M、N.
(1)、求证: ;(2)、若 , ,求 的长.52. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于M、N.
 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.53. 如图,在平行四边形 中,点E、F分别在 、 上, 与 相交于点O,且 .
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.53. 如图,在平行四边形 中,点E、F分别在 、 上, 与 相交于点O,且 . (1)、求证: ≌ ;(2)、连接 、 ,则四边形 (填“是”或“不是”)平行四边形.54. 如图,线段 ,射线 , 为射线 上一点,以 为边作正方形 ,且点 、 与点 在 两侧,在线段 上取一点 ,使 ,直线 与线段 相交于点 (点 与点 、 不重合).
(1)、求证: ≌ ;(2)、连接 、 ,则四边形 (填“是”或“不是”)平行四边形.54. 如图,线段 ,射线 , 为射线 上一点,以 为边作正方形 ,且点 、 与点 在 两侧,在线段 上取一点 ,使 ,直线 与线段 相交于点 (点 与点 、 不重合).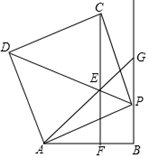 (1)、求证: ;(2)、判断 与 的位置关系,并说明理由;(3)、求 的周长.55. 如图,把平行四边形纸片 沿 折叠,点 落在点 处, 与 相交于点 .
(1)、求证: ;(2)、判断 与 的位置关系,并说明理由;(3)、求 的周长.55. 如图,把平行四边形纸片 沿 折叠,点 落在点 处, 与 相交于点 .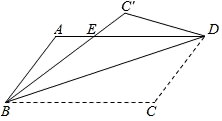 (1)、连接 ,则 与 的位置关系是;(2)、 与 相等吗?证明你的结论.56. 如图,将平行四边形纸片 沿一条直线折叠,使点 与点 重合,点 落在点 处,折痕为 .求证:
(1)、连接 ,则 与 的位置关系是;(2)、 与 相等吗?证明你的结论.56. 如图,将平行四边形纸片 沿一条直线折叠,使点 与点 重合,点 落在点 处,折痕为 .求证: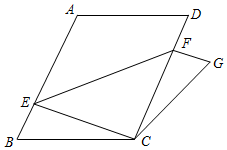 (1)、 ;(2)、 .57. 如图,四边形 中, ,点 、 分别在 上, ,过点 、 分别作 的垂线,垂足为 、 .
(1)、 ;(2)、 .57. 如图,四边形 中, ,点 、 分别在 上, ,过点 、 分别作 的垂线,垂足为 、 .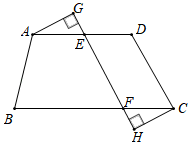 (1)、求证: ;(2)、连接 ,线段 与 是否互相平分?请说明理由.58. 如图,矩形 中, , ,点 、 分别在 、 上,且 .
(1)、求证: ;(2)、连接 ,线段 与 是否互相平分?请说明理由.58. 如图,矩形 中, , ,点 、 分别在 、 上,且 .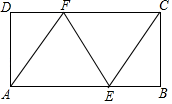 (1)、求证:四边形 是菱形;(2)、求线段 的长.
(1)、求证:四边形 是菱形;(2)、求线段 的长.