江苏中考数学历年真题分类卷16 数据的收集、整理与分析
试卷更新日期:2021-09-27 类型:二轮复习
一、单选题
-
1. 第七次全国人民普查的部分结果如图所示.

根据该统计图,下列判断错误的是( )
A、徐州0-14岁人口比重高于全国 B、徐州15-59岁人口比重低于江苏 C、徐州60岁以上人口比重高于全国 D、徐州60岁以上人口比重高于江苏2. 以下调查中,适宜全面调查的是( )A、了解全班同学每周体育锻炼的时间 B、调查某批次汽车的抗撞击能力 C、调查春节联欢晚会的收视率 D、鞋厂检测生产的鞋底能承受的弯折次数3. 已知一组数据:58,53,55,52,54,51,55,这组数据的中位数和众数分别是( )A、54,55 B、54,54 C、55,54 D、52,554. 已知一组数据:4,3,4,5,6,则这组数据的中位数是( )A、3 B、3.5 C、4 D、4.55. 为增强学生的环保意识,共建绿色文明校园.某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况如下表;班级
一班
二班
三班
四班
五班
废纸重量( )
4.5
4.4
5.1
3.3
5.7
则每个班级回收废纸的平均重量为( )
A、 B、 C、 D、6. 小红连续 天的体温数据如下(单位相 ): , , , , .关于这组数据下列说法正确的是( )A、中位数是 B、众数是 C、平均数是 D、极差是7. 已知一组数据5,4,4,6,则这组数据的众数是( )A、4 B、5 C、6 D、88. 一组数据2,4,6,x,3,9的众数是3,则这组数据的中位数是( )A、3 B、3.5 C、4 D、4.59. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:调查问卷 ________年________月________日
你平时最喜欢的一种体育运动项目是( )(单选)
A. B. C. D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是( )
A、①②③ B、①③⑤ C、②③④ D、②④⑤10. 已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )A、24,25 B、24,24 C、25,24 D、25,2511. 党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据, 年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法错误的是( ) A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务
A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务二、填空题
-
12. 某班按课外阅读时间将学生分为3组,第1、2组的频率分别为0.2、0.5,则第3组的频率是 .13. 一组数据2,0,2,1,6的众数为.14. 某射手在一次训练中共射出了10发子弹,射击成绩如图所示,则射击成绩的中位数是环.
 15. 小丽的笔试成绩为100分,面试成绩为90分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是分.16. 现有一组数据4、5、5、6、5、7,这组数据的众数是.17. 已知一组数据:a、4、5、6、7的平均数为5,则这组数据的中位数是.18. 一组数据2,1,3,1,2,4的中位数是.19. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.20. 今年6月6日是第25个全国爱眼日,某校从八年级随机抽取50名学生进行了视力调查,并根据视力值绘制成统计图(如图),这50名学生视力的中位数所在范围是.
15. 小丽的笔试成绩为100分,面试成绩为90分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是分.16. 现有一组数据4、5、5、6、5、7,这组数据的众数是.17. 已知一组数据:a、4、5、6、7的平均数为5,则这组数据的中位数是.18. 一组数据2,1,3,1,2,4的中位数是.19. 在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为.20. 今年6月6日是第25个全国爱眼日,某校从八年级随机抽取50名学生进行了视力调查,并根据视力值绘制成统计图(如图),这50名学生视力的中位数所在范围是.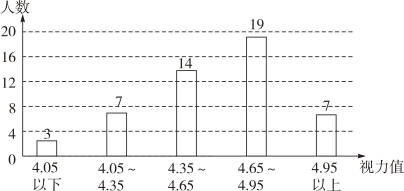 21. 一组数据 的平均数为.
21. 一组数据 的平均数为.三、综合题
-
22. 某市近年参加初中学业水平考试的人数(以下简称“中考人数”)的情况如图所示.
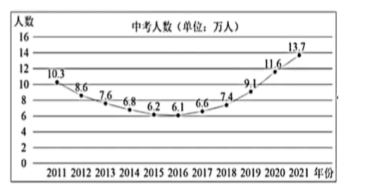
根据图中信息,解决下列问题:
(1)、这11年间,该市中考人数的中位数是万人;(2)、与上年相比,该市中考人数增加最多的年份是年;(3)、下列选项中,与该市2022年中考人数最有可能接近的是( )A、12.8万人 ; B、14.0万人; C、15.3万人(4)、2019年上半年,该市七、八、九三个年级的学生总数约为( )A、23.1万人; B、28.1万人; C、34.4万人(5)、该市2019年上半年七、八、九三个年级的数学教师共有4000人,若保持数学教师与学生的人数之比不变,根据(3)(4)的结论,该市2020年上半年七、八、九三个年级的数学教师较上年同期增加多少人(结果取整数)?23. 近5年,我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例,将这3种家电2016~2020年的产量(单位:万台)绘制成如图所示的折线统计图,图中只标注了甲种家电产量的数据.
观察统计图回答下列问题:
(1)、这5年甲种家电产量的中位数为 万台;(2)、若将这5年家电产量按年份绘制成5个扇形统计图,每个统计图只反映该年这3种家电产量占比,其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°,这个扇形统计图对应的年份是 年;(3)、小明认为:某种家电产量的方差越小,说明该家电发展趋势越好.你同意他的观点吗?请结合图中乙、丙两种家电产量变化情况说明理由.24. 某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.甲、乙两种西瓜得分表
序号
1
2
3
4
5
6
7
甲种西瓜(分)
75
85
86
88
90
96
96
乙种西瓜(分)
80
83
87
90
90
92
94
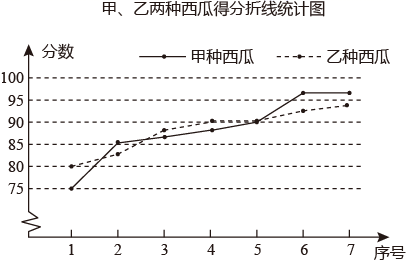
甲、乙两种西瓜得分统计表
平均数
中位数
众数
甲种西瓜
88
a
96
乙种西瓜
88
90
b
(1)、 , ;(2)、从方差的角度看,种西瓜的得分较稳定(填“甲”或“乙”);(3)、小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.25. 为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如下统计图. (1)、本次调查的样本容量是;(2)、补全条形统计图;(3)、已知该小区有居民2000人,请估计该小区对垃圾分类知识“完全了解”的居民人数.26. 为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:
(1)、本次调查的样本容量是;(2)、补全条形统计图;(3)、已知该小区有居民2000人,请估计该小区对垃圾分类知识“完全了解”的居民人数.26. 为了防控新冠疫情,某地区积极推广疫苗接种工作,卫生防疫部门对该地区八周以来的相关数据进行收集整理,绘制得到如下图表:该地区每周接种疫苗人数统计表
周次
第1周
第2周
第3周
第4周
第5周
第6周
第7周
第8周
接种人数(万人)
7
10
12
18
25
29
37
42
该地区全民接种疫苗情况扇形统计图
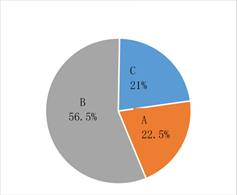
A:建议接种疫苗已接种人群
B:建议接种疫苗尚未接种人群
C:暂不建议接种疫苗人群
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3周开始这些点大致分布在一条直线附近,现过其中两点 、 作一条直线(如图所示,该直线的函数表达式为 ),那么这条直线可近似反映该地区接种人数的变化趋势.
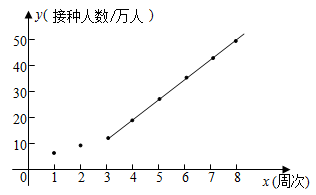
请根据以上信息,解答下列问题:
(1)、这八周中每周接种人数的平均数为万人:该地区的总人口约为万人;(2)、若从第9周开始,每周的接种人数仍符合上述变化趋势.①估计第9周的接种人数约为 ▲ 万人;
②专家表示:疫苗接种率至少达60%,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
(3)、实际上,受疫苗供应等客观因素,从第9周开始接种人数将会逐周减少 万人,为了尽快提高接种率,一旦周接种人数低于20万人时,卫生防疫部门将会采取措施,使得之后每周的接种能力一直维持在20万人.如果 ,那么该地区的建议接种人群最早将于第几周全部完成接种?27. 某企业为推进全民健身活动,提升员工身体素质,号召员工开展健身锻炼活动,经过两个月的宣传发动,员工健身锻炼的意识有了显著提高.为了调查本企业员工上月参加健身锻炼的情况,现从1500名员工中随机抽取200人调查每人上月健身锻炼的次数,并将调查所得的数据整理如下:某企业员工参加健身锻炼次数的频数分布表
锻炼次数x(代号)
(A)
(B)
(C)
(D)
(E)
(F)
频数
10
a
68
c
24
6
频率
0.05
b
0.34
d
0.12
0.03
某企业员工参加健身锻炼次数的扇形统计图
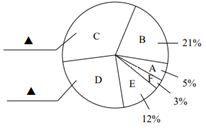 (1)、表格中 ;(2)、请把扇形统计图补充完整;(只需标注相应的数据)(3)、请估计该企业上月参加健身锻炼超过10次的员工有多少人?28. 如表是第四至七次全国人口普查的相关数据.
(1)、表格中 ;(2)、请把扇形统计图补充完整;(只需标注相应的数据)(3)、请估计该企业上月参加健身锻炼超过10次的员工有多少人?28. 如表是第四至七次全国人口普查的相关数据.年份
我国大陆人口总数
其中具有大学文化程度的人数
每10万大陆人口中具有大学文化程度的人数
1990年
1133682501
16124678
1422
2000年
1265830000
45710000
3611
2010年
1339724852
119636790
8930
2020年
1411778724
218360767
15467
(1)、设下一次人口普查我国大陆人口共a人,其中具有大学文化程度的有b人,则该次人口普查中每10万大陆人口中具有大学文化程度的人数为;(用含有a,b的代数式表示)(2)、如果将2020年大陆人口中具有各类文化程度(含大学、高中、初中、小学、其他)的人数分布制作成扇形统计图,求其中表示具有大学文化程度类别的扇形圆心角的度数;(精确到1°)(3)、你认为统计“每10万大陆人口中具有大学文化程度的人数”这样的数据有什么好处?(写出一个即可)29. 市环保部门为了解城区某一天18:00时噪声污染情况,随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计,把所抽取的测量数据分成A、B、C、D、E五组,并将统计结果绘制了两幅不完整的统计图表.组别
噪声声级x/dB
频数
A
55≤x<60
4
B
60≤x<65
10
C
65≤x<70
m
D
70≤x<75
8
E
75≤x<80
n
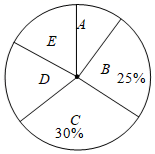
请解答下列问题:
(1)、m= , n=;(2)、在扇形统计图中D组对应的扇形圆心角的度数是°;(3)、若该市城区共有400个噪声测量点,请估计该市城区这一天18:00时噪声声级低于70dB的测量点的个数.30. 某机构为了解宿迁市人口年龄结构情况,对宿迁市的人口数据进行随机抽样分析,绘制了如下尚不完整的统计图表:类别
A
B
C
D
年龄(t岁)
0≤t<15
15≤t<60
60≤t<65
t≥65
人数(万人)
4.7
11.6
m
2.7

根据以上信息解答下列问题:
(1)、本次抽样调查,共调查了万人;(2)、请计算统计表中m的值以及扇形统计图中“C”对应的圆心角度数;(3)、宿迁市现有人口约500万人,请根据此次抽查结果,试估计宿迁市现有60岁及以上的人口数量.31. 某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如下表:序号
1
2
…
25
26
…
50
51
…
75
76
…
99
100
月均用水量/t
1.3
1.3
…
4.5
4.5
…
6.4
6.8
…
11
13
…
25.6
28
(1)、求这组数据的中位数.已知这组数据的平均数为 ,你对它与中位数的差异有什么看法?(2)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?32. 某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程.为了解学生对这四门课程的选择情况,学校从八年级全体学生中随机抽取部分学生进行问卷调查.并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出). 请你根据以上信息解决下列问题:(1)、参加问卷调查的学生人数为 ▲ 名.补全条形统计图(画图并标注相应数据);(2)、在扇形统计图中,选择“陶艺”课程的学生占%;(3)、若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?33. 为推进扬州市“青少年茁壮成长工程”,某校开展“每日健身操”活动,为了解学生对“每日健身操”活动的喜欢程度,随机抽取了部分学生进行调查,将调查信息结果绘制成如下尚不完整的统计图表:
请你根据以上信息解决下列问题:(1)、参加问卷调查的学生人数为 ▲ 名.补全条形统计图(画图并标注相应数据);(2)、在扇形统计图中,选择“陶艺”课程的学生占%;(3)、若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?33. 为推进扬州市“青少年茁壮成长工程”,某校开展“每日健身操”活动,为了解学生对“每日健身操”活动的喜欢程度,随机抽取了部分学生进行调查,将调查信息结果绘制成如下尚不完整的统计图表:抽样调查各类喜欢程度人数分布扇形统计图
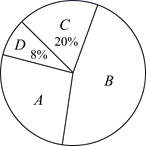
A.非常喜欢 B.比较喜欢 C.无所谓 D.不喜欢
抽样调查各类喜欢程度人数统计表
喜欢程度
人数
A.非常喜欢
50人
B.比较喜欢
m人
C.无所谓
n人
D.不喜欢
16人
根据以上信息,回答下列问题:
(1)、本次调查的样本容量是;(2)、扇形统计图中表示A程度的扇形圆心角为 ,统计表中 ;(3)、根据抽样调查的结果,请你估计该校2000名学生中大约有多少名学生喜欢“每日健身操”活动(包含非常喜欢和比较喜欢).34. 端午节吃粽子是中华民族的传统习俗.某食品厂为了解市民对去年销量较好的A、B、C、D四种粽子的喜爱情况,在端午节前对某小区居民进行抽样调查(每人只选一种粽子),并将调查情况绘制成如下两幅尚不完整的统计图.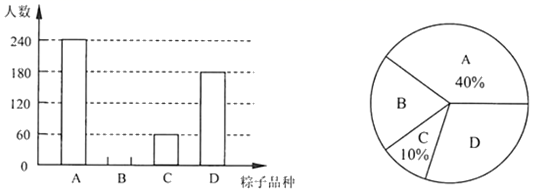
根据以上信息,解答下列问题:
(1)、补全条形统计图;(2)、扇形统计图中,D种粽子所在扇形的圆心角是 ;(3)、这个小区有2500人,请你估计爱吃B种粽子的人数为.35. 某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如下尚不完整的统计图表:市民每天的阅读时间统计表
类别
阅读时间
频数
450
400
50
市民每天的类别阅读时间扇形统计图
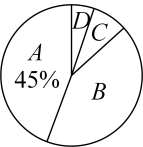
根据以上信息解答下列问题:
(1)、该调查的样本容量为 , ;(2)、在扇形统计图中,“ ”对应扇形的圆心角等于 ;(3)、将每天阅读时间不低于 的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.36. 教育部发布的义务教育质量监测结果报告显示,我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%.某校数学社团成员采用简单随机抽样的方法,抽取了本校八年级50名学生,对他们一周内平均每天的睡眠时间t(单位:小时)进行了调查,将数据整理后绘制成下表:平均每天的睡眠时间分组
5≤t<6
6≤t<7
7≤t<8
8≤t<9
9小时及以上
频数
1
5
m
24
n
该样本中学生平均每天的睡眠时间达9小时及以上的比例高于全国的这项数据,达到了22%.
(1)、求表格中n的值;(2)、该校八年级共400名学生,估计其中平均每天的睡眠时间在7≤t<8这个范围内的人数是多少.37. 某校计划成立下列学生社团.社团名称
文学社
动漫创作社
合唱团
生物实验小组
英语俱乐部
社团代号
A
B
C
D
E
为了解该校学生对上述社团的喜爱情况,学校从全体学生中随机抽取部分学生进行问卷调查(每名学生必需选一个且只能选一个学生社团).根据统计数据,绘制了如图条形统计图和扇形统计图(部分信息未给出).
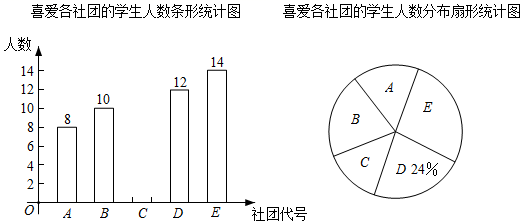 (1)、该校此次共抽查了名学生;(2)、请补全条形统计图(画图后标注相应的数据);(3)、若该校共有1000名学生,请根据此次调查结果,试估计该校有多少名学生喜爱英语俱乐部?38. 为了解全校学生对“垃圾分类”知识的掌握情况,某初级中学的两个兴趣小组分别抽样调查了100名学生.为方便制作统计图表,对“垃圾分类”知识的掌握情况分成四个等级:A表示“优秀”,B表示“良好”,C表示“合格”,D表示“不合格”.第一小组认为,八年级学生对“垃圾分类”知识的掌握不如九年级学生,但好于七年级学生,所以他们随机调查了100名八年级学生.
(1)、该校此次共抽查了名学生;(2)、请补全条形统计图(画图后标注相应的数据);(3)、若该校共有1000名学生,请根据此次调查结果,试估计该校有多少名学生喜爱英语俱乐部?38. 为了解全校学生对“垃圾分类”知识的掌握情况,某初级中学的两个兴趣小组分别抽样调查了100名学生.为方便制作统计图表,对“垃圾分类”知识的掌握情况分成四个等级:A表示“优秀”,B表示“良好”,C表示“合格”,D表示“不合格”.第一小组认为,八年级学生对“垃圾分类”知识的掌握不如九年级学生,但好于七年级学生,所以他们随机调查了100名八年级学生.第二小组随机调查了全校三个年级中的100名学生,但只收集到90名学生的有效问卷调查表.
两个小组的调查结果如图的图表所示:
第二小组统计表
等级
人数
百分比
A
17
18.9%
B
38
42.2%
C
28
31.1%
D
7
7.8%
合计
90
100%

若该校共有1000名学生,试根据以上信息解答下列问题:
(1)、第小组的调查结果比较合理,用这个结果估计该校学生对“垃圾分类”知识掌握情况达到合格以上(含合格)的共约人;(2)、对这两个小组的调查统计方法各提一条改进建议.39. 在某次疫情发生后,根据疾控部门发布的统计数据,绘制出如下统计图:图 为A地区累计确诊人数的条形统计图,图 为B地区新增确诊人数的折线统计图.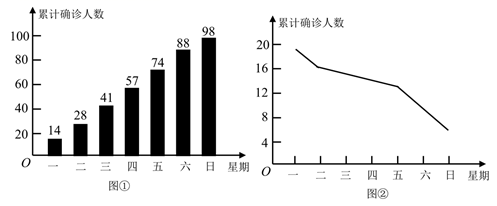 (1)、根据图 中的数据,A地区星期三累计确诊人数为 , 新增确诊人数为;(2)、已知A地区星期一新增确诊人数为14人,在图 中画出表示A地区新增确诊人数的折线统计图.(3)、你对这两个地区的疫情做怎样的分析,推断?40. 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.
(1)、根据图 中的数据,A地区星期三累计确诊人数为 , 新增确诊人数为;(2)、已知A地区星期一新增确诊人数为14人,在图 中画出表示A地区新增确诊人数的折线统计图.(3)、你对这两个地区的疫情做怎样的分析,推断?40. 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.
根据以上信息,回答下列问题:
(1)、本次调查的样本容量是 , 扇形统计图中表示A等级的扇形圆心角为 ;(2)、补全条形统计图;(3)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.41. 为了了解某地居民的用电量情况,随机抽取了该地200户居民六月份的用电量(单位: )进行调查,整理样本数据得到下面的频数分布表:组别
用电量分组
频数
1
50
2
100
3
34
4
11
5
1
6
1
7
2
8
1
根据抽样调查的结果,回答下列问题:
(1)、该地这200户居民六月份的用电量的中位数落在第组内.(2)、估计该地1万户居民六月份的用电量低于 的大约有多少户.