安徽省芜湖市无为市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 下列四个银行标志中,既是轴对称图形又是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、3. 下列说法中错误的是( )A、掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是 B、从装有10个红球的袋子中,摸出1个白球是不可能事件 C、为了解一批日光灯的使用寿命,可采用抽样调查的方式 D、某种彩票的中奖率为1%,买100张彩票一定有1张中奖4. 随着“新冠”疫情防控进入常态化,为了做好个人防护,学校要求学生每天上、放学途中必须佩戴口罩.小明和小亮两人家里都购买了相同数量的淡蓝色和白色一次性医用防护口罩,并且两人每天都随机选择口罩颜色,则某天上学小明和小亮都选择佩戴白色口罩的概率是( )A、 B、 C、 D、5. 小明同学是一位古诗文的爱好者,在学习了一元二次方程这一章后,改编 了苏轼诗词《念奴娇·赤壁怀古》:“大江东去浪淘尽,千古风流人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿同.哪位学子算得快,多少年华数周瑜?”假设周瑜去世时年龄的十位数字是 ,则可列方程为( )A、 B、 C、 D、6. 如图, 、 切 于点 、 ,点 是 上一点,且 ,则 的大小是( )
2. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、3. 下列说法中错误的是( )A、掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是 B、从装有10个红球的袋子中,摸出1个白球是不可能事件 C、为了解一批日光灯的使用寿命,可采用抽样调查的方式 D、某种彩票的中奖率为1%,买100张彩票一定有1张中奖4. 随着“新冠”疫情防控进入常态化,为了做好个人防护,学校要求学生每天上、放学途中必须佩戴口罩.小明和小亮两人家里都购买了相同数量的淡蓝色和白色一次性医用防护口罩,并且两人每天都随机选择口罩颜色,则某天上学小明和小亮都选择佩戴白色口罩的概率是( )A、 B、 C、 D、5. 小明同学是一位古诗文的爱好者,在学习了一元二次方程这一章后,改编 了苏轼诗词《念奴娇·赤壁怀古》:“大江东去浪淘尽,千古风流人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿同.哪位学子算得快,多少年华数周瑜?”假设周瑜去世时年龄的十位数字是 ,则可列方程为( )A、 B、 C、 D、6. 如图, 、 切 于点 、 ,点 是 上一点,且 ,则 的大小是( ) A、 B、 C、 D、7. 如图,点 是反比例函数 的图象上的一点,过点 作 ,使点 , 在 轴上,点 在 轴上,则 的面积为( )
A、 B、 C、 D、7. 如图,点 是反比例函数 的图象上的一点,过点 作 ,使点 , 在 轴上,点 在 轴上,则 的面积为( ) A、2 B、3 C、6 D、128. 反比例函数 ( 为常数)的图象上有三个点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、9. 如图,将含有 锐角的三角板 绕 的锐角顶点 逆时针旋转一个角度到 ,若 、 相交于点 , ,则旋转角是( )
A、2 B、3 C、6 D、128. 反比例函数 ( 为常数)的图象上有三个点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、9. 如图,将含有 锐角的三角板 绕 的锐角顶点 逆时针旋转一个角度到 ,若 、 相交于点 , ,则旋转角是( )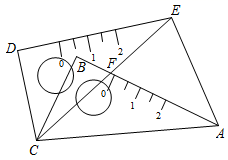 A、 B、 C、 D、10. 如图,抛物线 的顶点和该抛物线与 轴的交点在一次函数 的图象上,它的对称轴是 ,有下列四个结论:① ;② ;③ ;④当 时, ,其中正确的结论是( )
A、 B、 C、 D、10. 如图,抛物线 的顶点和该抛物线与 轴的交点在一次函数 的图象上,它的对称轴是 ,有下列四个结论:① ;② ;③ ;④当 时, ,其中正确的结论是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 抛物线 的顶点坐标为 .12. 已知反比例函数y= 的图象,在同一象限内,y随x的增大而增大,则n的取值范围是.13. 如图,菱形 中,已知 , 将它绕着点 逆时针旋转得到菱形 ,使 与 重合,则点 运动的路线 的长为 .
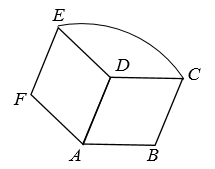 14. 如图,已知矩形 中 , ,将三角板的直角顶点 放在矩形内,移动三角板保持两直角边分别经过点 、 ,则 的最小值为 .
14. 如图,已知矩形 中 , ,将三角板的直角顶点 放在矩形内,移动三角板保持两直角边分别经过点 、 ,则 的最小值为 .
三、解答题
-
15. 解方程:16. 已知, 在直角坐标系内,三个顶点的坐标分别为 、 、 (正方形网格中每个小正方形的边长是一个单位长度)

⑴请画出 关于 轴的对称图形 ;
⑵请画出 以点 为旋转中心,逆时针旋转 所得的 .
17. 如图,已知圆锥的底面积为 ,高 ,求该圆锥的侧面展开图的面积(结果保留 ). 18. 年年底以来,“新冠疫情在全球肆虐,由于我国政府措施得当,疫情得到控制.而某些国家不够重视,导致疫情持续蔓延.若某国一社区开始有2人感染发病,未加控制,结果两天后发现共有50人感染发病.(1)、求每位发病者平均每天传染多少人?(2)、若疫情得不到有效控制,按照这样的传染速度,再过一天发病人数会超过200人吗?19. 小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
18. 年年底以来,“新冠疫情在全球肆虐,由于我国政府措施得当,疫情得到控制.而某些国家不够重视,导致疫情持续蔓延.若某国一社区开始有2人感染发病,未加控制,结果两天后发现共有50人感染发病.(1)、求每位发病者平均每天传染多少人?(2)、若疫情得不到有效控制,按照这样的传染速度,再过一天发病人数会超过200人吗?19. 小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况. (1)、若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?(2)、若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.20. 如图, 是 的内接三角形, 是弦 的中点,点 是 外一点且 ,连接 延长与圆相交于点 ,与 相交于点 .
(1)、若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?(2)、若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.20. 如图, 是 的内接三角形, 是弦 的中点,点 是 外一点且 ,连接 延长与圆相交于点 ,与 相交于点 .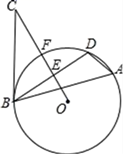 (1)、求证: 是 的切线;(2)、若 的半径为6, ,求弦 的长.21. 已知 、 两点是反比例函数 与一次函数 图象的两个交点.
(1)、求证: 是 的切线;(2)、若 的半径为6, ,求弦 的长.21. 已知 、 两点是反比例函数 与一次函数 图象的两个交点. (1)、求一次函数和反比例函数的解析式;(2)、求 的面积;(3)、观察图象,直接写出不等式 的解集.22. 在水果销售旺季,某水果店购进一批优质水果,进价为 元/千克,利润不低于 ,且不超过 ,根据销售情况(如下表),发现该水果一天的销售量 (千克)与该天的售价 (元/千克)满足一次函数关系.
(1)、求一次函数和反比例函数的解析式;(2)、求 的面积;(3)、观察图象,直接写出不等式 的解集.22. 在水果销售旺季,某水果店购进一批优质水果,进价为 元/千克,利润不低于 ,且不超过 ,根据销售情况(如下表),发现该水果一天的销售量 (千克)与该天的售价 (元/千克)满足一次函数关系.售价x(元/千克)
22.6
24
25.2
26
销售量y(千克)
34.8
32
29.6
28
(1)、某天这种水果的售价为24.5元/千克,求当天该水果的销售量.(2)、如果某天销售这种水果获利168元,那么该天水果的售价为多少元?(3)、售价定为多少元时,每天可获得最大利润?最大日利润是多少元?23. 如图,在平面直角坐标系中,点 的坐标是 .试寻找一些点,使他们满足“到点 与到 轴的距离相等”.小明在探究过程中首先想到了 的中点 满足条件,点 到点 和 轴的距离都是 .接着,小明过 轴上一点 作 轴的垂线 .他认为在 上应该有一个点 到点 与到 轴的距离相等.
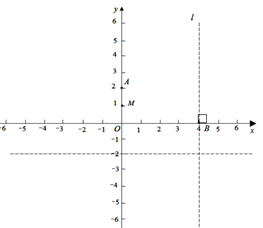 (1)、请你用尺规作图找出点 (不写画法,保留作图痕迹)并求出点 的坐标;(2)、小明用同样的方法又找出了一些符合条件的点,并把这些点用平滑的曲线连接起来他发现这些点在一条对称轴为 轴的抛物线上.请你根据以上探究和发现,求出这条抛物线的解析式;(3)、请直接写出平面内到点 和直线 距离相等的点所在抛物线的解析式.
(1)、请你用尺规作图找出点 (不写画法,保留作图痕迹)并求出点 的坐标;(2)、小明用同样的方法又找出了一些符合条件的点,并把这些点用平滑的曲线连接起来他发现这些点在一条对称轴为 轴的抛物线上.请你根据以上探究和发现,求出这条抛物线的解析式;(3)、请直接写出平面内到点 和直线 距离相等的点所在抛物线的解析式.