安徽省芜湖市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（　　）

A、戴口罩讲卫生 B、勤洗手勤通风 C、有症状早就医 D、少出门少聚集

查看试题解析
2. 如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为（）

A、5 B、4 C、3 D、2

查看试题解析
3. 如图，一个斜边长为 $6 cm$ 的红色直角三角形纸片，一个斜边长为 $10 cm$ 的蓝色直角三角形纸片，一张黄色的正方形纸片，拼成一个直角三角形，则红、蓝两张纸片的面积之和是（）

A、 $30 {cm}^{2}$ B、 $40 {cm}^{2}$ C、 $50 {cm}^{2}$ D、 $60 {cm}^{2}$

查看试题解析
4. 如图， $△ A B C$ 的三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将 $△ A B C$ 绕点B顺时针旋转到 $△ A^{'} B^{'} C^{'}$ 的位置，且点 $A^{'}$ 、 $C^{'}$ 仍落在格点上，则线段 $A B$ 扫过的图形的面积是（）平方单位（结果保留）

A、 $\frac{25 π}{4}$ B、 $\frac{13 π}{4}$ C、 $\frac{13 π}{2}$ D、 $\frac{13 π}{6}$

查看试题解析
5. 成语“水中捞月”所描述的事件是（）.

A、必然事件 B、随机事件 C、不可能事件 D、无法确定

查看试题解析
6. 如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA，OB的长分别是一元二次方程x²-7x+12=0的两个根（OA>OB)，在直线BC上取点P，使ΔPCD为等腰三角形，则点P的坐标为（）

A、（3，0） B、(7，3) C、(11，6） D、(11，6)或（3，0）

查看试题解析
7. 某种植基地2017年蔬菜产量为80吨，预计2019年蔬菜产量达到100吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为x ，则可列方程为（）．

A、 $80 {(1 + x)}^{2} = 100$ B、 $100 {(1 - x)}^{2} = 80$ C、 $80 {(1 + 2 x)}^{2} = 100$ D、 $80 {(1 - x)}^{2} = 100$

查看试题解析
8. 若关于x 的一元二次方程ax²＋2x－ $\frac{1}{2}$ ＝0（a＜0）有两个不相等的实数根，则a的取值范围是（）

A、a＜－2 B、a＞－2 C、－2＜a＜0 D、－2≤a＜0

查看试题解析
9. 如图，在等边三角形网格中，△ABC的顶点都在格点上，点P，Q，M是AB与格线的交点，则△ABC的外心是（）

A、点P B、点Q C、点M D、点N

查看试题解析
10. 如图，四边形ABCD为正方形，若 $AB = 4$ ，E是AD边上一点 $($ 点E与点A、D不重合 $)$ ，BE的中垂线交AB于M，交DC于N，设 $AE = x$ ，则图中阴影部分的面积S与x的大致图象是 $($ $)$

A、 B、 C、 D、

查看试题解析

二、填空题

11. 点( $- 1$ ,2)关于原点对称的点的坐标是.

查看试题解析
12. 如图，A、B是双曲线y＝ $\frac{k}{x}$ 的一个分支上的两点，且点B(a，b)在点A的右侧，则b的取值范围是．

查看试题解析
13. 设 $a - b = 2 + \sqrt{3}$ ， $b - c = 2 - \sqrt{3}$ ，则 $2 a^{2} + 2 b^{2} + 2 c^{2} - 2 a b - 2 a c - 2 b c =$ ．

查看试题解析
14. 已知 $⊙ O$ 的两条半径 $O A$ 与 $O B$ 相互垂直， $C$ 为优弧 $A B$ 上一点，且满足 $A B^{2} + O B^{2} = B C^{2}$ ，则 $∠ O A C =$ 度．

查看试题解析

三、解答题

15. 解方程： $x^{2} - 2 x - 15 = 0$ ．

查看试题解析
16. 如图，一圆弧过正方形网格的格点 $A$ 、 $B$ 、 $C$ ，现在方格中建立平面直角坐标系，使得点 $A$ 的坐标为 $(- 3 ， 2)$

⑴请画出平面直角坐标系；

⑵请你仅用一把无刻度的直尺，利用网格找出该圆弧的圆心 $P$ ，并直接写出圆心 $P$ 的坐标．（保留必要的作图痕迹）

查看试题解析
17. 宋代数学家杨辉所著《杨辉算法》中有一题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何？”译文为：一块矩形田地的面积为864平方步，只知道它的长与宽共60步，问它的长比宽多了多少步？

查看试题解析
18. 如图，已知某二次函数的顶点坐标是 $(1 ， - 4)$ ，且经过点 $A (4 ， 5)$

(1)、求该二次函数的表达式；

(2)、点 $P (m ， n)$ 是该二次函数图象上一点，若点 $P$ 到 $y$ 轴的距离不大于4，请根据图象直接写出 $n$ 的取值范围．

查看试题解析
19. 如图，一次函数 $y = - x + b$ 的图象与 $x$ 轴交于 $A$ 点，与 $y$ 轴交于 $B$ 点，与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $E (1 ， 5)$ 和点 $F$ ．

(1)、求 $k$ ， $b$ 的值以及点 $F$ 的坐标；

(2)、求 $△ E O F$ 的面积；

(3)、请根据函数图象直接写出反比例函数值大于一次函数值时 $x$ 的范围．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A B C$ 的平分线 $B E$ 交 $A C$ 于点 $E$ ，过点 $E$ 作 $B E$ 的垂线交 $A B$ 于点 $F$ ， $⊙ O$ 是 $△ B E F$ 的外接圆， $B C$ 与 $⊙ O$ 交于点 $D$ ．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、过点 $E$ 作 $E H ⊥ A B$ 于点 $H$ ，求证： $C D = H F$ ．

查看试题解析
21. 国家为了实现2020年全面脱贫目标，实施“精准扶贫”战略，采取易地搬迁，产业扶持等措施．使贫困户的生活条件得到改善，生活质量明显提高．某旗县为了全面了解贫困县对扶贫工作的满意度情况，进行随机抽样调查，分为四个类别：A．非常满意；B．满意；C．基本满意；D．不满意．依据调查数据绘制成图1和图2的统计图（不完整）．

根据以上信息，解答下列问题：

(1)、将图1补充完整；

(2)、通过分析，贫困户对扶贫工作的满意度（A、B、C类视为满意）是；

(3)、市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中，随机抽取两户进行满意度回访，求这两户贫困户恰好都是同一乡镇的概率．

查看试题解析
22. 某体育用品商店试销一款成本为50元的排球，规定试销期间单价不低于成本价，且获利不得高于40%．经试销发现，销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．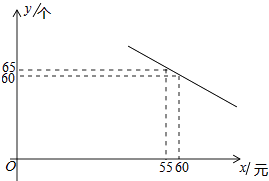

(1)、试确定y与x之间的函数关系式；

(2)、若该体育用品商店试销的这款排球所获得的利润Q元，试写出利润Q（元）与销售单价x（元）之间的函数关系式；当试销单价定为多少元时，该商店可获最大利润？最大利润是多少元？

(3)、若该商店试销这款排球所获得的利润不低于600元，请确定销售单价x的取值范围．

查看试题解析
23. 如图1，点 $E$ 为正方形 $A B C D$ 内一点， $∠ A E B = 90 °$ ，现将 $Rt △ A B E$ 绕点 $B$ 按顺时针方向旋转 $90 °$ ，得到 $△ C B E^{'}$ （点 $A$ 的对应点为点 $C$ ），延长 $A E$ 交 $C E^{'}$ 于点 $F$ ．

(1)、如图1，求证：四边形 $B E F E^{'}$ 是正方形；

(2)、连接 $D E$ ．
①如图2，若 $D A = D E$ ，求证： $F$ 为 $C E^{'}$ 的中点；

②如图3，若 $A B = 15$ ， $C F = 3$ ，试求 $D E$ 的长．

查看试题解析