安徽省铜陵市铜官区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、2x﹣3y+1 B、3x+y＝z C、x²﹣5x＝1 D、x²﹣ $\frac{1}{x}$ +2＝0

查看试题解析
2. 下列图形中，成中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 抛物线y＝﹣3（x﹣1）²+3的顶点坐标是（）

A、（﹣1，﹣3） B、（﹣1，3） C、（1，﹣3） D、（1，3）

查看试题解析
4. 下列成语所描述的是随机事件的是（）

A、竹篮打水 B、瓜熟蒂落 C、海枯石烂 D、不期而遇

查看试题解析
5. 对于双曲线y= $\frac{1 - m}{x}$ ，当x>0时，y随x的增大而减小，则m的取值范围为（）

A、m>0 B、m>1 C、m<0 D、m<1

查看试题解析
6. 若 $x = - 1$ 是关于x的一元二次方程 $a x^{2} + b x + 2 = 0 (a \neq 0)$ 的一个根，则 $2021 - 2 a + 2 b =$ （）

A、2025 B、2023 C、2019 D、2017

查看试题解析
7. 二次函数 $y = x^{2} + 4 x + 5$ 的图象可以由二次函数 $y = x^{2}$ 的图象平移而得到，下列平移正确的是（）

A、先向右平移2个单位，再向上平移1个单位 B、先向右平移2个单位，再向下平移1个单位 C、先向左平移2个单位，再向上平移1个单位 D、先向左平移2个单位，再向下平移1个单位

查看试题解析
8. 如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝25°．将△ABC绕点C顺时针旋转α角（0°＜α＜180°）至△A'B'C使得点A′恰好落在AB边上，则α等于（）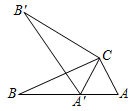

A、55° B、50° C、65° D、60°

查看试题解析
9. 如图，正六边形ABCDEF内接于 $⊙ O$ ，已知 $⊙ O$ 的半径为2，则圆心O到边AB的距离是（）

A、2 B、1 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

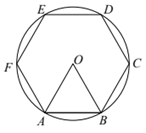查看试题解析
10. 已知点A（﹣1，﹣1），点B（1，1），若抛物线y＝x²﹣ax+a+1与线段AB有两个不同的交点（包含线段AB端点），则实数a的取值范围是（）

A、 $- \frac{3}{2}$ ≤a＜﹣1 B、 $- \frac{3}{2}$ ≤a≤﹣1 C、 $- \frac{3}{2}$ ＜a＜﹣1 D、 $- \frac{3}{2}$ ＜a≤﹣1

查看试题解析

二、填空题

11. 从五个数1，2，3，4，5中随机抽出1个数，则数3被抽中的概率为．

查看试题解析
12. 已知点 $A (x - 2, 3)$ 与 $B (x + 4, y - 5)$ 关于原点对称，则 $x y$ 的值是.

查看试题解析
13. 如图，AB是 $⊙ O$ 的弦，AC与 $⊙ O$ 相切于点A ，连接OA ， OB ，若 $∠ A O B = 130 °$ ，则 $∠ B A C =$ ．

查看试题解析
14. 如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y＝ $\frac{k}{x}$ (k≠0，x＞0)的图象经过顶点C、D，若点C的横坐标为5，BE＝3DE，则k的值为．

查看试题解析
15. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列5个结论：① $a b c > 0$ ；② $4 a + 2 b + c > 0$ ；③ ${(a + c)}^{2} > b^{2}$ ；④ $2 c < 3 b$ ；⑤ $a + b > m (a m + b)$ （ $m \neq 1$ 的实数）．其中正确的结论有．（填写序号）

查看试题解析

三、解答题

16. 解下列方程：

(1)、x²+2x﹣3＝0；

(2)、x（x﹣4）＝12﹣3x．

查看试题解析
17. 已知 $A (a ， - 2 a)$ 、 $B (- 2 ， a)$ 两点是反比例函数 $y = \frac{m}{x}$ 与一次函数 $y = k x + b$ 图象的两个交点．

(1)、求一次函数和反比例函数的解析式；

(2)、观察图象，直接写出不等式 $k x + b - \frac{m}{x} > 0$ 的解集．

查看试题解析
18. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．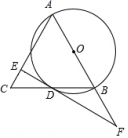

(1)、判断直线DE与⊙O的位置关系，并说明理由；

(2)、如果AB=5，BC=6，求DE的长．

查看试题解析
19. 抛物线 $y = - x^{2} + x + b$ 与x轴交于A、B两点，与y轴交于点C ，已知点B坐标为 $(2 ， 0)$ ．

(1)、求实数b的值；

(2)、若点D是抛物线在第一象限内图象上的点，求 $△ C B D$ 面积的最大值，及此时点D的坐标．

查看试题解析
20. 为了解疫情期网学生网络学习的学习效果，东坡中学随机抽取了部分学生进行调查．要求每位学生从“优秀”、“良好”、“一般”、“不合格”四个等次中，选择一项作为自我评价网络学习的效果现将调查结果绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

(1)、这次活动共抽查了人．

(2)、将条形统计图补充完整，并计算出扇形统计图中，学习效果“一般”的学生人数所在扇形的圆心角度数．

(3)、张老师在班上随机抽取了4名学生，其中学习效果“优秀”的1人，“良好”的2人，“一般”的1人，若再从这4人中随机抽取2人，请用画树状图法，求出抽取的2人学习效果全是“良好”的概率．

查看试题解析
21. 某服装厂生产 $A$ 品种服装，每件成本为71元，零售商到此服装厂一次性批发 $A$ 品牌服装 $x$ 件时，批发单价为 $y$ 元， $y$ 与 $x$ 之间满足如图所示的函数关系，其中批发件数 $x$ 为10的正整数倍．

(1)、当 $100 \leq x \leq 300$ 时， $y$ 与 $x$ 的函数关系式为．

(2)、某零售商到此服装厂一次性批发 $A$ 品牌服装200件，需要支付多少元？

(3)、零售商到此服装厂一次性批发 $A$ 品牌服装 $x (100 \leq x \leq 400)$ 件，服装厂的利润为 $w$ 元，问： $x$ 为何值时， $w$ 最大？最大值是多少？

查看试题解析
22. 边长为4的正方形ABCD绕顶点A ，按顺时针方向旋转至正方形 $A B_{1} C_{1} D_{1}$ ，记旋转角为 $α$ ．

(1)、如图1，当 $α = 60 °$ 时，求弧 $\overset{⌢}{C C_{1}}$ 的长度和线段AC扫过的扇形面积；

(2)、如图2，当 $α = 45 °$ 时，记BC与 $D_{1} C_{1}$ 的交点为E ，求线段 $D_{1} E$ 的长度；

(3)、如图3，在旋转过程中，若F为线段 $C B_{1}$ 的中点，求线段DF长度的取值范围．

查看试题解析