安徽省桐城市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 已知 是 的弦, 的半径为r , 下列关系式一定成立的是( )A、 B、 C、 D、2. 如图,平面直角坐标系中的点P的坐标为 , 与x轴正半轴的夹角为 ,则 的值为( )
 A、 B、 C、 D、3. 已知 ,则 的值为( )A、 B、 C、 D、4. 下列说法正确的是( )A、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 B、平分弦的直径垂直于弦,并且平分弦所对的弧 C、垂直于半径的直线是圆的切线 D、等弦所对的弧相等5. 已知二次函数 ,且 ,下列说法正确的是( )A、此函数的最大值为3 B、当 时,函数有最大值-6 C、函数y的取值范围是 D、函数y的取值范围是6. 如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( )
A、 B、 C、 D、3. 已知 ,则 的值为( )A、 B、 C、 D、4. 下列说法正确的是( )A、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 B、平分弦的直径垂直于弦,并且平分弦所对的弧 C、垂直于半径的直线是圆的切线 D、等弦所对的弧相等5. 已知二次函数 ,且 ,下列说法正确的是( )A、此函数的最大值为3 B、当 时,函数有最大值-6 C、函数y的取值范围是 D、函数y的取值范围是6. 如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( ) A、 B、 C、 D、247. 如图, 中, 的垂直平分线交 于E , 交 于D , 若 , ,则 的长是( )
A、 B、 C、 D、247. 如图, 中, 的垂直平分线交 于E , 交 于D , 若 , ,则 的长是( )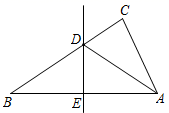 A、3 B、4 C、5 D、68. 已知二次函数 ( 的常数)的图象顶点为P , 下列说法正确的是( )A、点P只能在第三象限 B、点P只能在第四象限 C、点P在x轴上方 D、点P在直线 的下方9. 如图, 是 的弦,过点O作 于E交 于C , 过点A作 的切线 交 的延长线于D , 连接 , .下列结论中,错误的是( )
A、3 B、4 C、5 D、68. 已知二次函数 ( 的常数)的图象顶点为P , 下列说法正确的是( )A、点P只能在第三象限 B、点P只能在第四象限 C、点P在x轴上方 D、点P在直线 的下方9. 如图, 是 的弦,过点O作 于E交 于C , 过点A作 的切线 交 的延长线于D , 连接 , .下列结论中,错误的是( )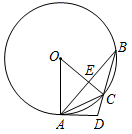 A、 平分 B、 C、 D、若 ,则10. 如图, 按顺时针方向旋转,点O在坐标原点上, 边在x轴上, , ,把 绕点A按顺时针方向转到 ,使得点 的坐标是 ,则在这次旋转过程中线段 扫过部分(阴影部分)的面积为( )
A、 平分 B、 C、 D、若 ,则10. 如图, 按顺时针方向旋转,点O在坐标原点上, 边在x轴上, , ,把 绕点A按顺时针方向转到 ,使得点 的坐标是 ,则在这次旋转过程中线段 扫过部分(阴影部分)的面积为( )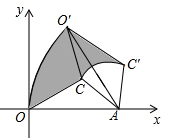 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 写出一个既是轴对称图形又是中心对称图形的几何图形,这个图形可以是 .12. 如图, 是 的直径,点A是 外一点,连接 交 于点E , 连接 并延长交 于点D , 若 ,则 的度数是 .
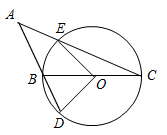 13. 若点 在抛物线 上,则a-b的最小值为 .14. 如图,在 的内接四边形 中, ,点E在弧 上,连接 、 、 、 .
13. 若点 在抛物线 上,则a-b的最小值为 .14. 如图,在 的内接四边形 中, ,点E在弧 上,连接 、 、 、 . (1)、 的度数为 .(2)、当 时, 恰好为 的内接正n边形的一边,则n的值为 .
(1)、 的度数为 .(2)、当 时, 恰好为 的内接正n边形的一边,则n的值为 .三、解答题
-
15. 如图,点A在反比例函数 的图象上,过点A作y轴的平行线交反比例函数 的图象于点B , 点C在y轴上,若 的面积为8,求k的值.
 16. 如图,点 是平行四边形 的边 的中点,连接 交对角线 于点 ,若 的面积为1,求平行四边形 的面积.
16. 如图,点 是平行四边形 的边 的中点,连接 交对角线 于点 ,若 的面积为1,求平行四边形 的面积. 17. 如图,由若干个边长为1的小正方形组成的网格中,已知格点线段 (端点是网格线的交点)和格点 .
17. 如图,由若干个边长为1的小正方形组成的网格中,已知格点线段 (端点是网格线的交点)和格点 . (1)、以点 为位似中心,画出线段 的位似图形线段 ,使线段 与线段 的相似比为2;(2)、以点 为旋转中心,画出线段 绕点 顺时针旋转90°得到的线段 .18. 已知抛物线 可由抛物线 平移得到,且经过点 .(1)、确定 的值;(2)、试确定该抛物线的顶点坐标.19. 如图, 是 的内接三角形.
(1)、以点 为位似中心,画出线段 的位似图形线段 ,使线段 与线段 的相似比为2;(2)、以点 为旋转中心,画出线段 绕点 顺时针旋转90°得到的线段 .18. 已知抛物线 可由抛物线 平移得到,且经过点 .(1)、确定 的值;(2)、试确定该抛物线的顶点坐标.19. 如图, 是 的内接三角形. (1)、用尺规作图确定圆心O的位置;(保留作图痕迹,不写作法)(2)、若 ,试确定 的半径.20. 如图,在某居民楼 楼顶悬挂“大国点名,没你不行”的横幅 ,在距楼底A点左侧水平距离 的D点处有一个斜坡,斜坡 的坡度 ,在坡底D点处测得居民楼楼顶B点的仰角为 ,在坡顶E点处测得居民楼楼顶横幅上端C点的仰角为27°(居民楼 ,横幅 与斜坡 的剖面在同一平面内),则横幅 的高度约为多少?(结果精确到0.1 ,参考数据: )
(1)、用尺规作图确定圆心O的位置;(保留作图痕迹,不写作法)(2)、若 ,试确定 的半径.20. 如图,在某居民楼 楼顶悬挂“大国点名,没你不行”的横幅 ,在距楼底A点左侧水平距离 的D点处有一个斜坡,斜坡 的坡度 ,在坡底D点处测得居民楼楼顶B点的仰角为 ,在坡顶E点处测得居民楼楼顶横幅上端C点的仰角为27°(居民楼 ,横幅 与斜坡 的剖面在同一平面内),则横幅 的高度约为多少?(结果精确到0.1 ,参考数据: )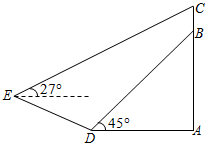 21. 从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线 .
21. 从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线 . (1)、如图1,在 中, , 是 的完美分割线,且 ,求 的度数.(2)、如图2,在 中, , , 是 的完美分割线,且 是以 为底边的等腰三角形,找出 与 的关系.
(1)、如图1,在 中, , 是 的完美分割线,且 ,求 的度数.(2)、如图2,在 中, , , 是 的完美分割线,且 是以 为底边的等腰三角形,找出 与 的关系.

