安徽省马鞍山市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y = - 2 x^{2} - 1$ 的顶点坐标是（）

A、 $(- 2 ， - 1)$ B、 $(2 ， 1)$ C、 $(0 ， - 1)$ D、 $(0 ， 1)$

查看试题解析
2. 若 $\frac{x}{x - y} = \frac{1}{2}$ ，则 $\frac{x}{y}$ 的值为（）

A、 $\frac{1}{2}$ B、-1 C、1 D、 $- \frac{1}{2}$

查看试题解析
3. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴相交于 $(- 2 ， 0)$ 和 $(4 ， 0)$ 两点，当函数值 $y < 0$ 时，自变量 $x$ 的取值范围是（）

A、 $x < - 2$ B、 $x > 4$ C、 $- 2 < x < 4$ D、 $x < - 2$ 或 $x > 4$

查看试题解析
4. 在一张缩印出来的纸上，一个三角形的一条边由原图中的6cm变成了2cm，则缩印出的三角形的面积是原图中三角形面积的（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{12}$

查看试题解析
5. 若点 $C$ 为线段 $A B$ 的黄金分割点，且 $A C > B C$ ，则下列各式中错误的是（）

A、 $A C = \frac{\sqrt{5} + 1}{2} A B$ B、 $B C = \frac{3 - \sqrt{5}}{2} A B$ C、 $A B = \frac{\sqrt{5} + 1}{2} A C$ D、 $A B ： A C = A C ： B C$

查看试题解析
6. 对于二次函数y＝ax²+bx+c（a≠0），我们把使函数值等于0的实数x叫做这个函数的零点，则二次函数y＝x²﹣mx﹣5（m为实数）的零点的个数是（）

A、1 B、2 C、0 D、不能确定

查看试题解析
7. 如图，在正方形方格纸中，每个小方格边长为1，A，B，C，D都在格点处，AB与CD相交于点O，则sin∠BOD的值等于（）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{3 \sqrt{10}}{10}$ C、 $\frac{2 \sqrt{10}}{5}$ D、 $\frac{\sqrt{10}}{5}$

查看试题解析
8. 若点（x₁ ， y₁）、（x₂ ， y₂）和（x₃ ， y₃）分别在反比例函数 $y = - \frac{2}{x}$ 的图象上，且 $x_{1} < x_{2} < 0 < x_{3}$ ，则下列判断中正确的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列结论：① $b^{2} - 4 a c > 0$ ；② $a b c > 0$ ；③ $4 a - 2 b + c > 0$ ；④ $3 a + c < 0$ ．其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，在Rt△ABC中，∠ACB = 90°，AC = BC = 4，CD⊥AB，垂足为D，E为BC的中点，AE与CD交于点F，则DF的长为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{3 \sqrt{2}}{4}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $\frac{7 \sqrt{2}}{10}$

查看试题解析

二、填空题

11. 某水库大坝高20米，背水坡的坡度为 $1 ： \sqrt{3}$ ，则背水坡的坡长为．

查看试题解析
12. 计算： $\sqrt{3} \cos^{2} 45 ° - \sin 30 ° \cdot \tan 60 ° =$ ．

查看试题解析
13. 如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形的三边长分别为3，4和x，那么x的值是．

查看试题解析
14. 如图，抛物线 $y = a x^{2} + c$ 与直线 $y = m x + n$ 交于 $A (- 2 ， - 3)$ ， $B (3 ， q)$ 两点，则不等式 $a x^{2} - m x + c < n$ 的解集是．

查看试题解析
15. 如图，在 $△ A B C$ 中， $D$ 在 $A C$ 边上， $A D ： D C = 1 ： 2$ ， $O$ 是 $B D$ 的中点，连接 $A O$ 并延长交 $B C$ 于点 $E$ ，若 $B E = 3$ ，则 $E C$ 的长为．

查看试题解析
16. 如图，双曲线 $y = \frac{k}{x} (x > 0)$ 经过 $A$ ， $B$ 两点，过点 $A$ 作 $A C ⊥ y$ 轴于点 $C$ ，过点 $B$ 作 $B D ⊥ y$ 轴于点 $D$ ，作 $B E ⊥ x$ 于点 $E$ ，连接 $A D$ ，如果 $A C = B E = 2$ ， $S_{四边形 B E O D} = 16$ ，那么 $Δ A C D$ 的面积： $S_{Δ A C D} =$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $C E ： E B = 1 ： 2$ ， $D E$ // $A C$ ，已知 $S_{△ A B C} = 1$ ，那么 $S_{△ A E D} =$ ．

查看试题解析
18. 当a﹣1≤x≤a时，函数y＝x²﹣2x+1的最小值为1，则a的值为.

查看试题解析

三、解答题

19. 如图，已知 $O$ 为坐标原点， $B$ ， $C$ 两点坐标为 $(3 ， - 1)$ ， $(2 ， 1)$ ．

(1)、在 $y$ 轴的左侧以 $O$ 点为位似中心将 $△ O B C$ 放大到原来的2倍，画出放大后 $△ O_{1} B_{1} C_{1}$ ；

(2)、写出 $B_{1} ， C_{1}$ 的坐标；

(3)、在（1）条件下，若 $△ O B C$ 内部有一点 $M$ 的坐标为 $(x ， y)$ ，请直接写出 $M$ 的对应点 $M_{1}$ 的坐标．

查看试题解析
20. 已知抛物线 $y = a x^{2} + b x - 3 (a \neq 0)$ 经过 $A (- 1 ， 0) ， B (3 ， 0)$ 两点， $C$ 点是抛物线与 $y$ 轴交点，直线 $l$ 是抛物线的对称轴．

(1)、求抛物线的函数解析式；

(2)、在抛物线的对称轴上是否存在一点 $M$ ，使得 $△ A C M$ 的周长最短？若存在，求点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析
21. 如图，一次函数y＝kx＋b的图象与反比例函数y＝ $\frac{m}{x}$ 的图象交于点A（－3，m＋8），B（n，－6）两点．

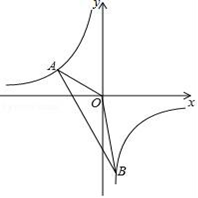(1)、求一次函数与反比例函数的解析式；

(2)、求△AOB的面积．

查看试题解析
22. 如图，某渔船在完成捕捞作业后准备返回港口C，途经某海域A处时，港口C的工作人员监测到点A在南偏东 $30 °$ 方向上，另一港口B的工作人员监测到点A在正西方向上．已知港口C在港口B的北偏西 $60 °$ 方向，且B、C两地相距120海里．

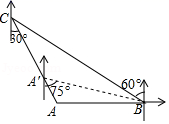(1)、求出此时点A到港口C的距离（计算结果保留根号）；

(2)、若该渔船从A处沿 $A C$ 方向向港口C驶去，当到达点 $A^{'}$ 时，测得港口B在 $A^{'}$ 的南偏东 $75 °$ 的方向上，求此时渔船的航行距离（计算结果保留根号）．

查看试题解析
23. 某超市经销一种商品，成本价为50元/千克．（规定每千克售价不低于成本价），且不高于85元，经市场调查发现，该种商品每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，部分数据如下表所示：

售价x（元/千克）

50

60

70

销售量y（千克）

120

100

800

(1)、求y（千克）与x（元/千克）之间的函数表达式；

(2)、为保证某天获得1600元的销售利润，则该天的销售单价应定为多少元？

(3)、当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？

查看试题解析
24. 如图，在△ABC中，∠ACB＝90°，CD是高，BE平分∠ABC．BE分别与AC，CD相交于点E，F．

(1)、求证：△AEB∽△CFB；

(2)、求证： $\frac{A E}{C E} = \frac{A B}{C B}$ ；

(3)、若CE＝5，EF＝2 $\sqrt{5}$ ，BD＝6．求AD的长．

查看试题解析

售价x（元/千克）	50	60	70
销售量y（千克）	120	100	800