安徽省六安市舒城县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 下列 关于 的函数中,属于二次函数的是( )A、 B、 C、 D、2. 若2x-5y=0,且xy≠0,则 ( )A、 B、 C、 D、3. 关于函数 ,下列说法中错误的是( )A、函数的图象在第二、四象限 B、y的值随x的值增大而增大 C、函数的图象与坐标轴没有交点 D、函数的图象关于原点对称4. 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
 A、 B、 C、 D、15. 如图在△ABC中,点D、E分别在△ABC的边AB、AC上,不一定能使△ADE与△ABC相似的条件是( )
A、 B、 C、 D、15. 如图在△ABC中,点D、E分别在△ABC的边AB、AC上,不一定能使△ADE与△ABC相似的条件是( )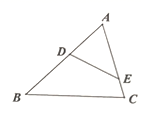 A、∠AED=∠B B、∠ADE=∠C C、 D、6. 已知点 , 在抛物线 上,则下列结论正确的是( )A、 B、 C、 D、7. 下列各式中正确的是( )A、 B、 C、 D、8. 如图,在 中, , 于 ,下列结论错误的有( )个
A、∠AED=∠B B、∠ADE=∠C C、 D、6. 已知点 , 在抛物线 上,则下列结论正确的是( )A、 B、 C、 D、7. 下列各式中正确的是( )A、 B、 C、 D、8. 如图,在 中, , 于 ,下列结论错误的有( )个①图中只有两对相似三角形;② ;③ ;④若 , ,则 .
 A、1个 B、2个 C、3个 D、4个9. 二次函数的 与 的部分对应值如表,则下列判断中正确的是( )
A、1个 B、2个 C、3个 D、4个9. 二次函数的 与 的部分对应值如表,则下列判断中正确的是( )…
0
1
3
4
…
…
2
4
2
-2
…
A、抛物线开口向上 B、 的最大值为4 C、当 时, 随 的增大而减小 D、当 时,10. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为 ,点D的坐标为 ,延长CB交x轴于点A1 , 作第1个正方形 ;延长 交x轴于点 ,作第2个正方形 …,按这样的规律进行下去,第2021个正方形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 请写出一个顶点在原点且开口向下的抛物线解析式 .12. 如图,在 的正方形网格中,每个小正方形的边长为1,连接两格点 , ,线段 与网格线的交点为点 ,则 .
 13. 如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例的数 在第一象限内的图象经过点D , 交BC于点E . 若 , , ,则D点的坐标是 .
13. 如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例的数 在第一象限内的图象经过点D , 交BC于点E . 若 , , ,则D点的坐标是 . 14. 如图,已知 , 为线段 上的一个动点,分别以 、 为边在 的同侧作菱形 和菱形 .点 、 、 在一条直线上, , , 别是对角线 、 的中点,当点 在线段 上移动时,点 、 之间的距离最短为 .
14. 如图,已知 , 为线段 上的一个动点,分别以 、 为边在 的同侧作菱形 和菱形 .点 、 、 在一条直线上, , , 别是对角线 、 的中点,当点 在线段 上移动时,点 、 之间的距离最短为 .
三、解答题
-
15. 计算: .16. 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
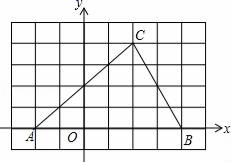 (1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)(2)、若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , , S△A′B′C′:S△ABC= .17. 如图,在 中, , 是 边上一点, , ,设 .
(1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)(2)、若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , , S△A′B′C′:S△ABC= .17. 如图,在 中, , 是 边上一点, , ,设 .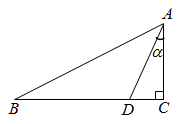 (1)、求 的值;(2)、若 ,求 的长.18. 如图,已知反比例函数 的图像与一次函数 的图像交于A(-1, ),B在( ,-3)两点.
(1)、求 的值;(2)、若 ,求 的长.18. 如图,已知反比例函数 的图像与一次函数 的图像交于A(-1, ),B在( ,-3)两点. (1)、求 的值;(2)、直接写出使一次函数值大于反比例函数值时x的取值范围.19. 已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A , B两点,且A点在B的右侧.(1)、当抛物线经过点(3,8),求a的值;(2)、求A、B两点的坐标;(3)、若抛物线的顶点为M , 且点M到x轴的距离等于AB的3倍,求抛物线的解析式.20. 如图,某大楼的顶部竖有一块宣传牌 .小明在山坡的坡脚 处测得宣传牌底部 的仰角为 ,沿山坡向上走到 处测得宣传牌顶部 的仰角为 .已知山坡 的坡度 , 米, 米.
(1)、求 的值;(2)、直接写出使一次函数值大于反比例函数值时x的取值范围.19. 已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A , B两点,且A点在B的右侧.(1)、当抛物线经过点(3,8),求a的值;(2)、求A、B两点的坐标;(3)、若抛物线的顶点为M , 且点M到x轴的距离等于AB的3倍,求抛物线的解析式.20. 如图,某大楼的顶部竖有一块宣传牌 .小明在山坡的坡脚 处测得宣传牌底部 的仰角为 ,沿山坡向上走到 处测得宣传牌顶部 的仰角为 .已知山坡 的坡度 , 米, 米.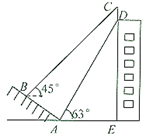 (1)、求点 距地面的高度;(2)、求大楼 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: , )21. 如图,在△ABC中,∠C=90°,AC=6cm,BC=8m,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)、求点 距地面的高度;(2)、求大楼 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: , )21. 如图,在△ABC中,∠C=90°,AC=6cm,BC=8m,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动. (1)、如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?(2)、如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?22. 果农周大爷家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,他记录了10天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如表所示:
(1)、如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?(2)、如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?22. 果农周大爷家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,他记录了10天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如表所示:
 (1)、请直接写出p与x的函数关系式及自变量x的取值范围;(2)、求y与x的函数关系式,并写出自变量x的取值范围;(3)、在这10天中,哪一天销售额达到最大,最大销售额是多少元.23. 如图, 是正方形 的边 延长线上一点,连接 ,过顶点 作 ,垂足为 , 交边 于点 .
(1)、请直接写出p与x的函数关系式及自变量x的取值范围;(2)、求y与x的函数关系式,并写出自变量x的取值范围;(3)、在这10天中,哪一天销售额达到最大,最大销售额是多少元.23. 如图, 是正方形 的边 延长线上一点,连接 ,过顶点 作 ,垂足为 , 交边 于点 .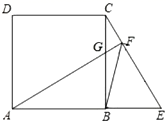 (1)、求证: .(2)、连接 ,求 的大小.(3)、过点 作 交 于点 ,求 的值.
(1)、求证: .(2)、连接 ,求 的大小.(3)、过点 作 交 于点 ,求 的值.