安徽省六安市金寨县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图, 是 的切线,切点为 , 的延长线交 于点 ,若 ,则 的度数为 ( )
2. 如图, 是 的切线,切点为 , 的延长线交 于点 ,若 ,则 的度数为 ( ) A、64° B、26° C、52° D、38°3. 共享单车为市民出行带来了方便,某单车公司第一个月投放 辆单车,计划第三个月投放单车 辆,若第二个月的增长率是 ,第三个月的增长率是第二个月的两倍,那么 与 的函数关系是 ( )A、 B、 C、 D、4. 已知点 在反比例函数 的图象上,若 ,则 的取值范围是 ( )A、 B、 C、 D、5. 如图,在 中, 两点分别在 上,且 平分 ,若 , 与 相交于点 ,则图中与 相似的是 ( )
A、64° B、26° C、52° D、38°3. 共享单车为市民出行带来了方便,某单车公司第一个月投放 辆单车,计划第三个月投放单车 辆,若第二个月的增长率是 ,第三个月的增长率是第二个月的两倍,那么 与 的函数关系是 ( )A、 B、 C、 D、4. 已知点 在反比例函数 的图象上,若 ,则 的取值范围是 ( )A、 B、 C、 D、5. 如图,在 中, 两点分别在 上,且 平分 ,若 , 与 相交于点 ,则图中与 相似的是 ( ) A、 B、 C、 D、6. 如图, 是 的直径, 是 上的三等分点,且 ,则 等于 ( )
A、 B、 C、 D、6. 如图, 是 的直径, 是 上的三等分点,且 ,则 等于 ( )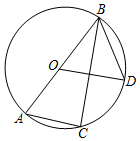 A、120° B、95° C、105° D、150°7. 如图, 是 的直径, 是弦,四边形 是菱形, 与 相交于点 ,则下列结论错误的是( )
A、120° B、95° C、105° D、150°7. 如图, 是 的直径, 是弦,四边形 是菱形, 与 相交于点 ,则下列结论错误的是( ) A、 B、 平分 C、 D、8. 如图,已知正方形 与正方形 的边长分别为4和1,若将正方形 绕点 旋转,则在旋转过程中,点 之间的最小距离为 ( )
A、 B、 平分 C、 D、8. 如图,已知正方形 与正方形 的边长分别为4和1,若将正方形 绕点 旋转,则在旋转过程中,点 之间的最小距离为 ( ) A、3 B、 C、 D、9. 如图,在由边长为1的小正方形组成的网格中,点 , , , 都在格点上,点 在 的延长线上,以 为圆心, 为半径画弧,交 的延长线于点 ,且弧 经过点 ,则扇形 的面积为( )
A、3 B、 C、 D、9. 如图,在由边长为1的小正方形组成的网格中,点 , , , 都在格点上,点 在 的延长线上,以 为圆心, 为半径画弧,交 的延长线于点 ,且弧 经过点 ,则扇形 的面积为( ) A、 B、 C、 D、10. 如图,在矩形 中, , 为 的中点,连接 分别是 上的点,且 .设 的面积为 , 的长为 ,则 关于 的函数关系式的图象大致是 ( )
A、 B、 C、 D、10. 如图,在矩形 中, , 为 的中点,连接 分别是 上的点,且 .设 的面积为 , 的长为 ,则 关于 的函数关系式的图象大致是 ( ) A、
A、 B、
B、 C、
C、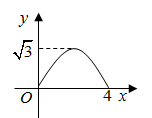 D、
D、
二、填空题
-
11. 在平面内, 的半径为 ,点 到圆心 的距离为 ,则点 与 的位置关系是点 在 . (填“圆内”“圆外”或“圆上”).12. 在平面直角坐标系中,点 关于原点对称的点的坐标为 .13. 圆锥的表面展开图由一个扇形和一个圆组成,已知扇形的半径为9,圆心角为120°,则圆锥的底面圆的半径为 .14. 如图,在正方形网格中建立平面直角坐标系,一条圆弧经过点 .
 (1)、若该圆弧所在圆的圆心为 ,则 的长为 .(2)、该圆弧的长为 .
(1)、若该圆弧所在圆的圆心为 ,则 的长为 .(2)、该圆弧的长为 .三、解答题
-
15. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),求 的余角的度数.
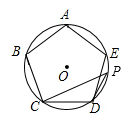 16. 如图,在等边 中, 是边 上的一点,连接 ,将 绕点 逆时针旋转60°得到 ,连接 .若 ,求 的周长.
16. 如图,在等边 中, 是边 上的一点,连接 ,将 绕点 逆时针旋转60°得到 ,连接 .若 ,求 的周长. 17. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的 ,且 .
17. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的 ,且 . (1)、将 绕点 顺时针旋转90°后得到 (其中 三点旋转后的对应点分别是 ),画出 .(2)、设 的内切圆的半径为 , 的外接圆的半径为 ,则 .18. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 上方150米的点 处悬停,此时测得桥两端 两点的俯角分别为65°和45°,求桥 的长度.(参考数据: , , ;结果精确到0.1米)
(1)、将 绕点 顺时针旋转90°后得到 (其中 三点旋转后的对应点分别是 ),画出 .(2)、设 的内切圆的半径为 , 的外接圆的半径为 ,则 .18. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 上方150米的点 处悬停,此时测得桥两端 两点的俯角分别为65°和45°,求桥 的长度.(参考数据: , , ;结果精确到0.1米) 19. 定义:若一次函数 和反比例函数 满足 ,则称 为一次函数和反比例函数的“等差”函数.(1)、 和 是否存在“等差”函数?若存在,请写出它们的“等差”函数.(2)、若 和 存在“等差”函数,且“等差”函数的图象与 的图象的一个交点的横坐标为1,求反比例函数的表达式.20. 如图,在平行四边形 中, ,将平行四边形绕点 顺时针旋转 得到平行四边形 .
19. 定义:若一次函数 和反比例函数 满足 ,则称 为一次函数和反比例函数的“等差”函数.(1)、 和 是否存在“等差”函数?若存在,请写出它们的“等差”函数.(2)、若 和 存在“等差”函数,且“等差”函数的图象与 的图象的一个交点的横坐标为1,求反比例函数的表达式.20. 如图,在平行四边形 中, ,将平行四边形绕点 顺时针旋转 得到平行四边形 . (1)、求点 到 的距离;(2)、当点 落在 边上时,求点 经过的路径长.21. 如图,在 中, ,以 为直径作 分别交 、 于点 、 两点,连接 ,点 为 延长线上一点,连接 ,若 ;
(1)、求点 到 的距离;(2)、当点 落在 边上时,求点 经过的路径长.21. 如图,在 中, ,以 为直径作 分别交 、 于点 、 两点,连接 ,点 为 延长线上一点,连接 ,若 ; (1)、求证: 为 切线;(2)、若 , ,求 半径.
(1)、求证: 为 切线;(2)、若 , ,求 半径.

