安徽省六安市金安区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 下列函数中,是二次函数的是( )A、 B、 C、 D、2. sin30°的值为( )A、 B、 C、 D、3. 在双曲线y= 的每一支上,y都随x的增大而减小,则k的取值范围是( )A、k>0 B、k>7 C、k<7 D、k<04. 二次函数 的图象与 轴的交点个数是( )A、1个 B、2个 C、0个 D、无法确定5. 下列各组线段中,成比例的是( )A、2cm,3cm,4cm,5cm B、2cm,4cm,6cm,8cm C、3cm,6cm,8cm,12cm D、1cm,3cm,5cm,15cm6. 在 中, ,则 的值为( )A、 B、 C、 D、7. 如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中共有相似三角形( )
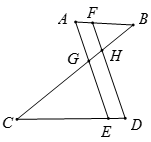 A、4对 B、5对 C、6对 D、7对8. 如图,传送带和地面所成斜坡 的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )
A、4对 B、5对 C、6对 D、7对8. 如图,传送带和地面所成斜坡 的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )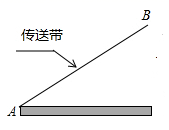 A、5米 B、 米 C、 米 D、 米9. 如图,直线 ,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , .若 ,则 的值为( )
A、5米 B、 米 C、 米 D、 米9. 如图,直线 ,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , .若 ,则 的值为( )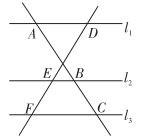 A、 B、 C、 D、10. 如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是( )
A、 B、 C、 D、10. 如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是( ) A、
A、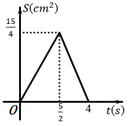 B、
B、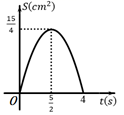 C、
C、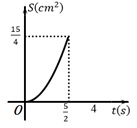 D、
D、
二、填空题
-
11. 抛物线 的顶点坐标为.12. 已知:点P是线段MN的黄金分割点,(PM>PN),MN=4cm,则MP=.13. 如图, , 与 相交于点 .若 , , ,则 的长为 .
 14. 如图,在矩形ABCD中,AC是矩形ABCD的对角线,并且AC平分∠DAE,AC=12cm,AD=9cm,动点P从点E出发,沿EA方向匀速运动,速度为1cm/s,同时动点Q从点C出发,沿CA方向匀速运动,速度为2cm/s,连接PQ,设运动时间为t(s)(0<t<6),则当t=时,△PQA为等腰三角形.
14. 如图,在矩形ABCD中,AC是矩形ABCD的对角线,并且AC平分∠DAE,AC=12cm,AD=9cm,动点P从点E出发,沿EA方向匀速运动,速度为1cm/s,同时动点Q从点C出发,沿CA方向匀速运动,速度为2cm/s,连接PQ,设运动时间为t(s)(0<t<6),则当t=时,△PQA为等腰三角形.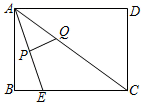
三、解答题
-
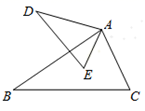
15. 计算: .16. 已知抛物线 .(1)、用配方法求出它的对称轴和顶点坐标;(2)、求出它与y轴的交点坐标.17. 如图,在 与 中, ,且 .
求证: .
 18. 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
18. 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.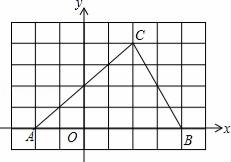 (1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)(2)、若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .19. 在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾xm,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,求出x的最小值.
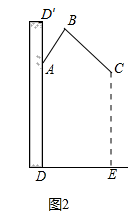
(1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)(2)、若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .19. 在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾xm,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,求出x的最小值.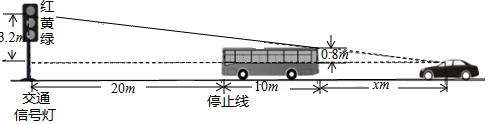 20. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点A处,手柄长 , AB与墙壁 的夹角 ,喷出的水流BC与AB形成的夹角 ,现在住户要求:当人站在E处淋浴时,水流正好喷洒在人体的C处,且使 问:安装师傅应将支架固定在离地面多高的位置?
20. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点A处,手柄长 , AB与墙壁 的夹角 ,喷出的水流BC与AB形成的夹角 ,现在住户要求:当人站在E处淋浴时,水流正好喷洒在人体的C处,且使 问:安装师傅应将支架固定在离地面多高的位置?(参考数据: ).

 21. 如图,抛物线 与x轴交于 和点 .
21. 如图,抛物线 与x轴交于 和点 .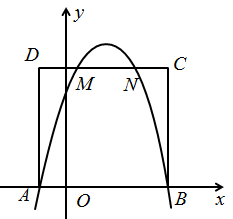 (1)、求该抛物线的表达式.(2)、以AB为边向上作矩形ABCD , 边CD与抛物线交于点M , N , 若 ,求矩形ABCD的周长.22. 2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为 ,销售量y(千克)与x之间的关系如图所示.
(1)、求该抛物线的表达式.(2)、以AB为边向上作矩形ABCD , 边CD与抛物线交于点M , N , 若 ,求矩形ABCD的周长.22. 2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为 ,销售量y(千克)与x之间的关系如图所示. (1)、求y与x之间的函数关系式,并写出x的取值范围;(2)、当月第几天,该农产品的销售额最大,最大销售额是多少?
(1)、求y与x之间的函数关系式,并写出x的取值范围;(2)、当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
23. 如图 (1)、如图1,在 中,D为AB上一点, .求证: ;(2)、如图2,在□ 中,E为BC上一点,F为CD延长线上一点, .若 , ,求AD的长.(3)、如图3,在菱形ABCD中,E是AB上一点,F是 内一点, , , , , ,求DF的长.
(1)、如图1,在 中,D为AB上一点, .求证: ;(2)、如图2,在□ 中,E为BC上一点,F为CD延长线上一点, .若 , ,求AD的长.(3)、如图3,在菱形ABCD中,E是AB上一点,F是 内一点, , , , , ,求DF的长.