安徽省合肥市瑶海区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线y=x²-2x+3的对称轴是（）

A、直线x=1 B、直线x=2 C、直线x=-1 D、直线x=-2

查看试题解析
2. 若反比例函数的图象经过（2，-2），（m，1），则m=（）

A、1 B、-1 C、4 D、-4

查看试题解析
3. 如图，D、E分别是△ABC边AB、AC上的点，且△ADE～△ACB，若AD=2，AB=6，AC=4，则AE的长是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 在Rt△ABC中，∠C=90°，cosA= $\frac{2}{3}$ ，AB=6．则AC的长为（）

A、8 B、6 C、4 D、2

查看试题解析
5. 如图，在⊙O中，∠BOC=54°，则∠BAC的度数为（）

A、27° B、28° C、36° D、54°

查看试题解析
6. 在平面直角坐标系中，抛物线y=x²+4x经变换后得到抛物线y=x²-4x，则这个变换可以是（）

A、向左平移4个单位 B、向右平移4个单位 C、向左平移8个单位 D、向右平移8个单位

查看试题解析
7. 如图钓鱼竿AC长6m ，露在水面上的鱼线BC长3 $\sqrt{2}$ m ，钓者想看看鱼钓上的情况，把鱼竿AC逆时针转动15°到AC′的位置，此时露在水面上的鱼线B'C'长度是（）

A、3m B、 $3 \sqrt{3}$ m C、 $2 \sqrt{3}$ m D、4m

查看试题解析
8. 如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，半径OA交小圆于点D，若OD=3，tan∠OAB= $\frac{\sqrt{3}}{3}$ ，则劣弧AB的长是（）

A、2π B、3π C、4π D、6π

查看试题解析
9. 抛物线y=kx²-1与双曲线 $y = \frac{k}{x} (k \neq 0)$ 在同平面直角坐标系中的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 已知抛物线y=x²+(2a-1)x+1-2a与x轴交于点A(x₁ ， 0)、B(x₂ ， 0)，且-1 $<$ x₁ $<$ 0，0 $<$ x₂ $< \frac{1}{2}$ ，则实数a的取值范围是（）

A、 $a > \frac{1}{2}$ B、 $a < \frac{3}{4}$ C、 $a > \frac{1}{2}$ 或 $a < \frac{3}{4}$ D、 $\frac{1}{2} < a < \frac{3}{4}$

查看试题解析

二、填空题

11. 写出命题“圆内接四边形的对角互补”的逆命题：．

查看试题解析
12. 如图，在 $5 \times 4$ 的正方形网格中，每个小正方形的边长都是1， $△ A B C$ 的顶点都在这些小正方形的顶点上，则 $\sin ∠ B A C$ 的值为．

查看试题解析
13. 如图，反比例函数 $y = \frac{6}{x} (x > 0)$ 与一次函数y=x-2的图象交于点P (a，b)，则 $\frac{1}{a} - \frac{1}{b}$ 的值为．

查看试题解析
14. 如图，点Q是△ABC内一点，且满足∠QAB=∠QBC=∠QCA=∠a．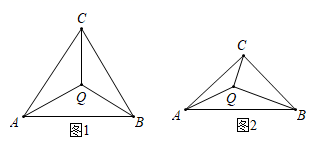

(1)、如图1，当△ABC是等边三角形时，∠a= ．

(2)、如图2，当△ABC 是等腰直角三角形(其中 ∠ACB=90°)时，△QAC、△QBA、△QCB的面积之比是．

查看试题解析

三、解答题

15. 计算：cos²30°+sin²45°﹣tan60°•tan30°

查看试题解析
16. 已知抛物线y=-x²+bx+c过点A(1，0)，B(-3，0)，求抛物线的解析式及其顶点C的坐标．

查看试题解析
17. 每个小方格是边长为1个单位长度的小正方形，菱形OABC在平面直角坐标系的位置如图所示．

⑴以O为位似中心，在第一象限内将菱形OABC放大为原来的2倍得到菱形OA₁B₁C₁ ，请画出菱形OA₁B₁C₁ ，并直接写出点B₁的坐标；

⑵将菱形OABC绕原点O顺时针旋转90°得到菱形OA₂B₂C₂ ，请画出菱形OA₂B₂C₂ ．

查看试题解析
18. 已知：如图，在△ABC中，D为AB中点，E为AC上一点，延长DE、BC交于点F．
求证：BF·EC=CF·AE．

查看试题解析
19. 为测量一古塔的高度，数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°，然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°，已知楼房高AB约是16m，试求该古塔的高度．(结果精确到0.1m，参考数据： $\sqrt{3}$ =1.73，sin65°≈0.91，cos65°≈0.42，tan65°≈2.14)

查看试题解析
20. 如图，点A在反比例函数 $y = \frac{k}{x}$ 的图象位于第一象限的分支上，过点A作AB⊥y轴于点B，S_△AOB=2．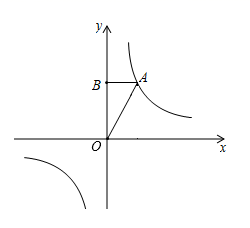

(1)、求该反比例函数的表达式，

(2)、若P(x₁ ， y₁)、Q(x₂ ， y₂)是反比例函数 $y = \frac{k}{x}$ 图象上的两点，且x₁ $<$ x₂ ， y₁ $<$ y₂ ，指出点P、Q各位于哪个象限，并简要说明理由．

查看试题解析
21. 已知：如图，AB是⊙O的直径，AC是⊙O的弦，点D是弧BC的中点，过点D作EF⊥AC的延长线于点E．

(1)、求证：EF是⊙O的切线；

(2)、若⊙O直径是5，AE=3.2，求BD的长．

查看试题解析
22. 安徽盒子健康公司不断加大科技投入，现投资500万元购进一条灭新冠病毒专用口罩生产线，2020年12月份投产后若不计维修保养、捐赠口罩成本等费用，每月可创利100万元．实际生产过程中，第n月的维修保养、捐赠口罩成本等费用满足下表：

第n月

第1月

第2月

维修保养、捐赠口罩成本等费用（万元）

3

5

若从第1月到第n月的维修保养与损耗等费用累计为y(万元)，且y=an²+bn．

(1)、求出y的解析式；

(2)、设该公司第n月的利润为w(万元)，求w与n之间的函数关系式，并指出在第几月w取得最大值，最大值是多少？

(3)、该公司在2021年哪月份能收回投资？

查看试题解析
23. 如图，点E是正方形ABCD内部一点，△AEF、△BEG均为等腰直角三角形，∠EAF=∠EBG=90°，连接AG、FC．

(1)、已知正方形的边长为5，E、F、G三点在同一条直线上(如图1)．
①若△AEF与△BEG的相似比为2：1，求△EAB的面积；

②求D、E两点之间距离的最小值．

(2)、如图2，当E、F、G三点不在同一条直线上时，求证：AG $//$ CF．

查看试题解析

第n月	第1月	第2月
维修保养、捐赠口罩成本等费用（万元）	3	5