安徽省合肥市庐阳区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 抛物线y=3(x﹣2)2+5的顶点坐标是( )A、(﹣2,5) B、(﹣2,﹣5) C、(2,5) D、(2,﹣5)2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、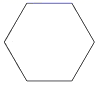 C、
C、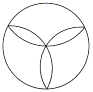 D、
D、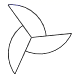 3. 若 ,则 的值( )A、 B、 C、﹣ D、﹣4. 要将抛物线 平移后得到抛物线 ,下列平移方法正确的是( )A、向左平移1个单位,再向上平移2个单位 B、向左平移1个单位,再向下平移2个单位 C、向右平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向下平移2个单位5. 如图,D、E在△ABC的边上,如果DE∥BC , AE:BE=1:2,BC=6,那么DE的长为( )
3. 若 ,则 的值( )A、 B、 C、﹣ D、﹣4. 要将抛物线 平移后得到抛物线 ,下列平移方法正确的是( )A、向左平移1个单位,再向上平移2个单位 B、向左平移1个单位,再向下平移2个单位 C、向右平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向下平移2个单位5. 如图,D、E在△ABC的边上,如果DE∥BC , AE:BE=1:2,BC=6,那么DE的长为( )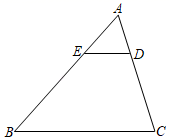 A、 B、2 C、 D、36.
A、 B、2 C、 D、36.如图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值等于( )
 A、 B、 C、 D、7. 如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A、 B、 C、 D、7. 如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )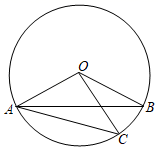 A、30° B、40° C、50° D、60°8. 已知等腰△ABC中,AB=AC=10,顶角∠A=36°,BD为∠ABC的平分线,则CD的长是( )
A、30° B、40° C、50° D、60°8. 已知等腰△ABC中,AB=AC=10,顶角∠A=36°,BD为∠ABC的平分线,则CD的长是( ) A、5 ﹣5 B、5 +5 C、15+5 D、15﹣59.
A、5 ﹣5 B、5 +5 C、15+5 D、15﹣59.二次函数的图象如图所示,反比例函数与一次函数在同一平面直角坐标系中的大致图象是( )
 A、
A、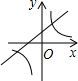 B、
B、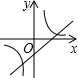 C、
C、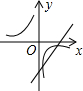 D、
D、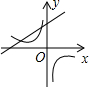 10. 如图,在Rt△ABC中,∠C=90°,AC=1,D是斜边AB的中点,E是边BC上一点,且DE平分△ABC的周长,则DE的长为( )
10. 如图,在Rt△ABC中,∠C=90°,AC=1,D是斜边AB的中点,E是边BC上一点,且DE平分△ABC的周长,则DE的长为( )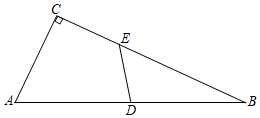 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
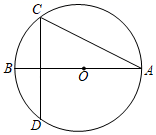
11. 比较大小:sin48°cos48°(填“>”、“<”或“=”).12. 如图,点B为弧CD上的中点,延长BO交⊙O于点A , AB=8,∠A=30°,CD的长为 .
 13. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数 的图象上,顶点B在反比例函数 的图象上,点C在x轴的正半轴上,则平行四边形OABC的面积是
13. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数 的图象上,顶点B在反比例函数 的图象上,点C在x轴的正半轴上,则平行四边形OABC的面积是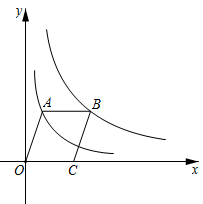 14. 抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是
14. 抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是三、解答题
-
15. 计算:sin245°+|tan60°﹣2|+2cos30°.16. 已知抛物线在x轴上所截线段的长为4,顶点坐标为(2,4),求此抛物线的解析式.17. 如图,在平面坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
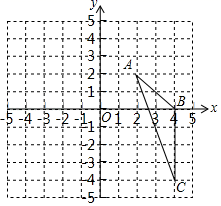 (1)、①请在图中,画出将△ABC绕点O逆时针旋转90°得到的△A1B1C1;
(1)、①请在图中,画出将△ABC绕点O逆时针旋转90°得到的△A1B1C1;②以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴右侧,画△A2B2C2;
(2)、tan∠BAC= .18. 如图所示,巡逻船在A处测得灯塔C在北偏东 方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东 方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km.参考数据: , , )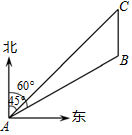 19. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是边BC上异于B、C的一个动点,过点D作∠ADE=45°,DE交AC于点E .
19. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是边BC上异于B、C的一个动点,过点D作∠ADE=45°,DE交AC于点E .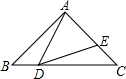 (1)、求证△ABD∽△DCE;(2)、设BD=x , AE=y , 求y与x之间的函数关系式,并求x的取值范围.20. 如图,点A(1,6),B(3,m)是直线AB与反比例函数 (x>0)的图象的两个交点,AC⊥x轴,垂足为C , 已知D(0,1),连接AD , BD , BC .
(1)、求证△ABD∽△DCE;(2)、设BD=x , AE=y , 求y与x之间的函数关系式,并求x的取值范围.20. 如图,点A(1,6),B(3,m)是直线AB与反比例函数 (x>0)的图象的两个交点,AC⊥x轴,垂足为C , 已知D(0,1),连接AD , BD , BC .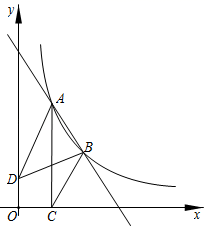 (1)、求直线AB的表达式;(2)、△ABC和△ABD的面积分别为S1 , S2 , 求S2﹣S1 .21. 如图,在△ABC中,BC是⊙O的直径,D是弧CE的中点.
(1)、求直线AB的表达式;(2)、△ABC和△ABD的面积分别为S1 , S2 , 求S2﹣S1 .21. 如图,在△ABC中,BC是⊙O的直径,D是弧CE的中点.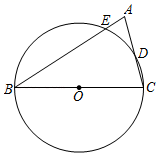 (1)、求证:AB=BC;(2)、若AD=3,AE=2,求BC的长.22. 任意球是足球比赛的主要得分手段之一.在某次足球赛中,甲球员站在点O处发出任意球,如图,把球看作点,其运行的高度y(m)与运行的水平距离x(m)满足关系式 ,已知防守队员组成的人墙与O点的水平距离为9m , 防守队员跃起后的高度为2.1m , 对方球门与O点的水平距离为18m , 球门高是2.43m . (假定甲球员的任意球恰好能射正对方的球门)
(1)、求证:AB=BC;(2)、若AD=3,AE=2,求BC的长.22. 任意球是足球比赛的主要得分手段之一.在某次足球赛中,甲球员站在点O处发出任意球,如图,把球看作点,其运行的高度y(m)与运行的水平距离x(m)满足关系式 ,已知防守队员组成的人墙与O点的水平距离为9m , 防守队员跃起后的高度为2.1m , 对方球门与O点的水平距离为18m , 球门高是2.43m . (假定甲球员的任意球恰好能射正对方的球门)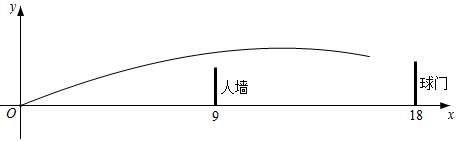 (1)、当h=3时,求y与x的关系式(不要求写出自变量x的取值范围);(2)、当h=3时,足球能否越过人墙?足球会不会踢飞(球从球门的上方飞过)?请说明理由.(3)、若甲球员发出的任意球直接射进对方球门得分,求h的取值范围.23. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)、当h=3时,求y与x的关系式(不要求写出自变量x的取值范围);(2)、当h=3时,足球能否越过人墙?足球会不会踢飞(球从球门的上方飞过)?请说明理由.(3)、若甲球员发出的任意球直接射进对方球门得分,求h的取值范围.23. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.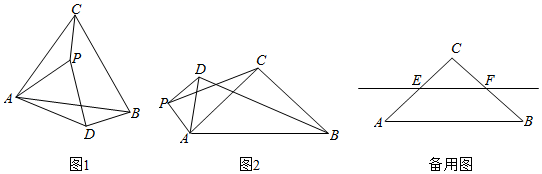 (1)、观察猜想
(1)、观察猜想如图1,当 时, 的值是 , 直线BD与直线CP相交所成的较小角的度数是 .
(2)、类比探究如图2,当 时,请写出 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)、解决问题当 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时 的值.