安徽省合肥市庐江县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形分别是四届国际数学家大会的会标，其中不属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列说法正确的是（）

A、可能性很大的事情是必然发生的 B、可能性很小的事情是不可能发生的 C、“掷一次骰子，向上一面的点数是6”是不可能事件 D、“任意画出一个平行四边形，它是中心对称图形”是必然事件

查看试题解析
3. 方程 $3 x (x - 1) = 2 (x - 1)$ 的根是（）

A、 $x = 1$ B、 $x = \frac{2}{3}$ C、 $x_{1} = 1 ， x_{2} = \frac{2}{3}$ D、 $x_{1} = 1 ， x_{2} = \frac{3}{2}$

查看试题解析
4. 将抛物线 $y = {(x + 1)}^{2} + 3$ 向右平移1个单位，再向下平移2个单位后，所得抛物线的解析式为（）

A、 $y = {(x + 2)}^{2}$ B、 $y = x^{2} + 1$ C、 $y = {(x + 2)}^{2} - 5$ D、 $y = x^{2} + 5$

查看试题解析
5. 已知抛物线 $y = x^{2} - x - 1$ 与x轴的一个交点为 $(m ， 0)$ ，则代数式 $m^{2} - m + 2021$ 的值为（）

A、2020 B、2021 C、2022 D、2023

查看试题解析
6. 如图，AB是⊙O的直径，PA切⊙O于点A，连接PO并延长交⊙O于点C，连接AC，AB＝10，∠P＝30°，则AC的长度是（）

A、5 $\sqrt{3}$ B、5 $\sqrt{2}$ C、5 D、 $\frac{5}{2}$

查看试题解析
7. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、560(1＋x)²＝315 B、560(1－x)²＝315 C、560(1－2x)²＝315 D、560(1－x²)＝315

查看试题解析
8. 如图，在同一平面内，将 $△ A B C$ 绕点A逆时针旋转 $40 °$ 到 $△ A E D$ 的位置，恰好使得 $D C // A B$ ，则 $∠ C A B$ 的大小为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
9. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，它与x轴的一个交点A在点 $（ 2 ， 0 ）$ 和点 $（ 3 ， 0 ）$ 之间，图象的对称轴是 $x = 1$ ，在下列说法中：① $a b < 0$ ；② $2 a + b = 0$ ；③ $3 a + c > 0$ ；④当 $- 1 < x < 3$ 时， $y > 0$ ．其中正确的说法有（）

A、①② B、①③ C、②③ D、①②④

查看试题解析
10. 如图，在扇形纸片 $O A B$ 中， $O A = 10 ， ∠ A O B = 36 ° ， O B$ 在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转（旋转过程中无滑动），当 $O A$ 落在l上时，停止旋转.则点O所经过的路线长为（）

A、 $13 π$ B、 $12 π$ C、 $11 π$ D、 $10 π$

查看试题解析

二、填空题

11. 关于x的方程（a﹣5）x²﹣4x﹣1=0有实数根，则a满足．

查看试题解析
12. 如图，A、B、C、D均在⊙O上，E为BC延长线上一点，若∠A=102°，则∠DCE= ．

查看试题解析
13. 已知抛物线为 $y_{1} = a {(x + m)}^{2} + k$ 与 $y_{2} = - a {(x - m)}^{2} - k (m \neq 0)$ 关于原点对称，我们称 $y_{1}$ 为与 $y_{2}$ 互为“和谐抛物线”，请写出抛物线 $y = - 4 x^{2} + 6 x + 7$ 的“和谐抛物线” ．

查看试题解析
14. 如图，点A、B、C、D分别在正方形网格的格点上，其中A点的坐标为（﹣1，5），B点的坐标为（3，3），小明发现，线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，则这个旋转中心的坐标是．

查看试题解析

三、解答题

15. 解方程： $- 4 x (3 x + 1) = 3 (3 x + 1)$ ．

查看试题解析
16. 如图，在 $⊙ O$ 中，直径 $A B$ 垂直弦 $C D$ ，垂足是点M， $A M = 18 ， B M = 8$ ，求弦 $C D$ 的长．

查看试题解析
17. 已知二次函数 $y = a x^{2} - 2 x + c$ 的图象经过点 $A (- 2 ， 0) 、 B (3 ， 0)$ ．

(1)、求二次函数的解析式；

(2)、求此抛物线的对称轴和顶点坐标．

查看试题解析
18. 如图，已知在⊙O中，AB=4 $\sqrt{3}$ ，AC是⊙O的直径，AC⊥BD于F，∠A=30°．

(1)、求图中阴影部分的面积；

(2)、若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．

查看试题解析
19. 在下列网格图中，每个小正方形的边长均为1个单位，在 $R t Δ A B C ， ∠ C = 90^{°} ， A C = 3 ， B C = 4$ ．

⑴在图中画出 $Δ A B C$ 以A为旋转中心，沿顺时针方向旋转 $90^{°}$ 后的图形 $Δ A B_{1} C_{1}$ ；

⑵若点B的坐标为 $(- 3 ， 5)$ ，点C的坐标为 $(- 3 ， 1)$ ，在图中建立直接坐标系，并画出 $Δ A B C$ 关于原点对称的图形 $A_{2} B_{2} C_{2}$ ．

查看试题解析
20. 某学校为了美化校园环境，向园林公司购买一批树苗．公司规定：若购买树苗不超过60棵，则每棵树苗售价120元；若购买树苗超过60棵，则每增加1棵，每棵树苗售价均降低0.5元，且每棵树苗的售价降到100元后，不管购买多少棵树苗，每棵树苗售价均为100元．如果该学校向园林公司支付树苗款8800元，那么这所学校购买了多少棵树苗？

查看试题解析
21. 在一次数学兴趣小组活动中，李燕和刘凯两位同学设计了如图所示的两个转盘做游戏（每个转盘被分成面积相等的几个扇形，并在每个扇形区域内标上数字）．游戏规则如下：两人分别同时转动甲、乙转盘，转盘停止后，若指针所指区域内两数和小于12，则李燕获胜；若指针所指区域内两数和等于12，则为平局；若指针所指区域内两数和大于12，则刘凯获胜（若指针停在等分线上，重转一次，直到指针指向某一份内为止）．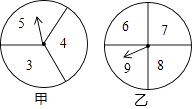

(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果；

(2)、分别求出李燕和刘凯获胜的概率．

查看试题解析
22.
如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．

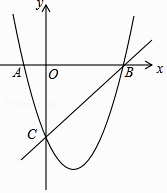(1)、求这个二次函数的解析式；

(2)、是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；

(3)、动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．

查看试题解析
23. 通过类比联想、引申拓展研究典型题目，可以达到解一题知一类题的目的，下面是一个案例，请补充完整．
原题；如图①，点 $E 、 F$ 分别在正方形 $A B C D$ 的边 $B C 、 C D$ 上， $∠ E A F = 45 °$ ，连接 $E F$ ，则 $E F = B E + D F$ ，试说明理由，

(1)、（思路梳理）
∵ $A B = A D$ ，∴把 $△ A B E$ 绕点A逆时针旋转 $90 °$ 至 $△ A D G$ ，可使 $A B$ 与 $A D$ 重合，∵ $∠ A D G = ∠ B = 90 °$ ，∴ $∠ F D G = 180 °$ ，即：点 $F 、 D 、 G$ 共线，根据“ $S A S$ ”，易证 $△ A F G ≌$ ，得 $E F = F G = B E + D F$ ；

(2)、（类比引申）
如图②，四边形 $A B C D$ 中， $A B = A D ， ∠ B A D = 90 °$ ，点 $E 、 F$ 分别在 $B C 、 C D$ 上， $∠ E A F = 45 °$ ，若 $∠ B ， ∠ D$ 都不是直角，则当 $∠ B$ 与 $∠ D$ 满足等量关系时，仍有 $E F = B E + D F$ ；

(3)、（联想拓展）
如图③，在 $△ A B C$ 中， $∠ B A C = 90 ° ， A B = A C$ ，点 $D 、 E$ 均在边 $B C$ 上，且 $∠ D A E = 45 °$ ，猜想 $B D ， D E ， E C$ 应满足的等量关系，并写出推理过程．

查看试题解析