安徽省阜阳市太和县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)2. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )
3. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )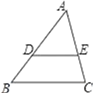 A、2 B、4 C、6 D、84. 如图,在△ABC中,∠C=90°,cosA= ,则sinB=( )
A、2 B、4 C、6 D、84. 如图,在△ABC中,∠C=90°,cosA= ,则sinB=( )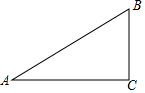 A、 B、 C、 D、5. 若 ,则 的值是( )A、 B、 C、 D、46. 将抛物线 先向左平移2个长度单位,再向上平移3个长度单位,所得到的抛物线是( )A、 B、 C、 D、7. 已知二次函数 中 与 的部分对应值如下表,下列说法正确的是( )
A、 B、 C、 D、5. 若 ,则 的值是( )A、 B、 C、 D、46. 将抛物线 先向左平移2个长度单位,再向上平移3个长度单位,所得到的抛物线是( )A、 B、 C、 D、7. 已知二次函数 中 与 的部分对应值如下表,下列说法正确的是( )﹣1
0
1
3
﹣3
1
3
1
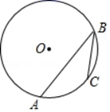
A、抛物线开口向上 B、其图象的对称轴为直线 C、当 时, 随 的增大而增大 D、方程 必有一个根大于48. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积= (弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )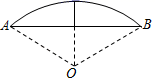 A、 B、 C、 D、9. 如图,四边形 是矩形,四边形 是边长为3的正方形,点 , 在 轴的正半轴上,点 在 轴的正半轴上,点 在边 上,点 、 在双曲线 上,且 ,则 值为( ).
A、 B、 C、 D、9. 如图,四边形 是矩形,四边形 是边长为3的正方形,点 , 在 轴的正半轴上,点 在 轴的正半轴上,点 在边 上,点 、 在双曲线 上,且 ,则 值为( ).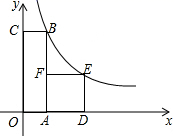 A、15 B、 C、 D、1710. 如图,矩形OABC的顶点A、C分别在x轴、y轴上,OA=4,OC=3,直线m:y=﹣ x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M , N , 直线m运动的时间为t(秒),设△OMN的面积为S , 则能反映S与t之间函数关系的大致图象是( )
A、15 B、 C、 D、1710. 如图,矩形OABC的顶点A、C分别在x轴、y轴上,OA=4,OC=3,直线m:y=﹣ x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M , N , 直线m运动的时间为t(秒),设△OMN的面积为S , 则能反映S与t之间函数关系的大致图象是( )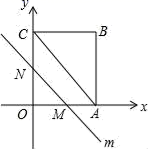 A、
A、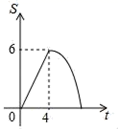 B、
B、 C、
C、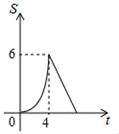 D、
D、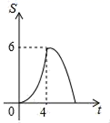
二、填空题
-
11. 如果函数y=x2m﹣1为反比例函数,则m的值是 .12. 如图, 的半径为5, 为弦,点C为 的中点,若 ,则弦 的长为 .
 13. 如图,利用标杆BE测量楼房CD的高度,如果标杆BE长为 米,若 ,BC=16.8米,则楼高是 .
13. 如图,利用标杆BE测量楼房CD的高度,如果标杆BE长为 米,若 ,BC=16.8米,则楼高是 .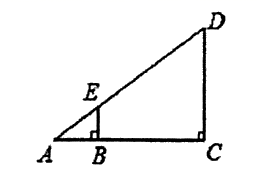 14. 如图,在▱ABCD 中,∠A=60°,AB=8,AD=6,点 E、F 分别是边 AB、CD 上的动点,将该四边形沿折痕 EF 翻折,使点 A 落在边 BC 的三等分点处,则 AE 的长为 .
14. 如图,在▱ABCD 中,∠A=60°,AB=8,AD=6,点 E、F 分别是边 AB、CD 上的动点,将该四边形沿折痕 EF 翻折,使点 A 落在边 BC 的三等分点处,则 AE 的长为 .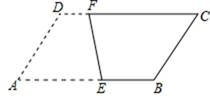
三、解答题
-
15. 求值:16. 已知一抛物线 和抛物线 的形状及开口方向完全相同,且经过点(1)、求此抛物线解析式;(2)、用配方法求此抛物线的顶点坐标.17. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).

⑴以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1 .
⑵画出△ABC绕C点逆时针旋转90°后得到的△A2B2C.
18. 如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,求CD的长.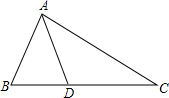 19. 根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
19. 根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°. (1)、计算AB的长度.(2)、通过计算判断此车是否超速.20. 水果种植大户小芳,为了吸引更多的顾客,组织了观光采摘游活动,每一位来采摘水果的顾客都有一次抽奖机会,在一只不透明的盒子里有A(苹果),B(梨子),C(葡萄),D(葡萄)四张外形完全相同的卡片,抽奖时先随机抽取一张卡片,再从盒子中剩下的3张中随机抽取第二张.(1)、请利用树状图或列表的方法,表示前后两次抽得的卡片所有可能的情况;(2)、如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?21. 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作⊙O的切线交AB的延长线于E,交BC于F.
(1)、计算AB的长度.(2)、通过计算判断此车是否超速.20. 水果种植大户小芳,为了吸引更多的顾客,组织了观光采摘游活动,每一位来采摘水果的顾客都有一次抽奖机会,在一只不透明的盒子里有A(苹果),B(梨子),C(葡萄),D(葡萄)四张外形完全相同的卡片,抽奖时先随机抽取一张卡片,再从盒子中剩下的3张中随机抽取第二张.(1)、请利用树状图或列表的方法,表示前后两次抽得的卡片所有可能的情况;(2)、如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?21. 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作⊙O的切线交AB的延长线于E,交BC于F. (1)、求证:DF⊥BC;(2)、求证:DE2=AE•BE.22. 某公司生产一种成本为20元/件的新产品,在2018年1月1日投放市场,前3个月是试销售,3个月后,正常销售.(1)、试销售期间,该产品的销售价格不低于20元/件,且不能超过80元/件,销售价格 (元/件)与月销售量 (万件)满足函数关系式 ,前3个月每件产品的定价多少元时,每月可获得最大利润?最大利润为多少?(2)、正常销售后,该种产品销售价格统一为 元/件,公司每月可销售 万件,从第4个月开始,每月可获得的最大利润是多少万元?23. 某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:
(1)、求证:DF⊥BC;(2)、求证:DE2=AE•BE.22. 某公司生产一种成本为20元/件的新产品,在2018年1月1日投放市场,前3个月是试销售,3个月后,正常销售.(1)、试销售期间,该产品的销售价格不低于20元/件,且不能超过80元/件,销售价格 (元/件)与月销售量 (万件)满足函数关系式 ,前3个月每件产品的定价多少元时,每月可获得最大利润?最大利润为多少?(2)、正常销售后,该种产品销售价格统一为 元/件,公司每月可销售 万件,从第4个月开始,每月可获得的最大利润是多少万元?23. 某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答: (1)、如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EFGH;(填“>”“=”或“<”)(2)、如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证: = ;(3)、如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
(1)、如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EFGH;(填“>”“=”或“<”)(2)、如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证: = ;(3)、如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.